最近在研究图计算的性能,需要构造不同的测试数据对图算法进行压测,其中就涉及到均匀图的概念。
因为做的是理论测试,因此就需要一种理论上绝对均匀的图测试数据,接下来我们就讨论一下绝对均匀图的生成。
一、何为绝对均匀图?
为了方便讨论,我们只讨论无向图,而且图中的边是无权值的,且两点之间只能存在一条边,即边仅代表结点之间的关联。
从图论角度出发,我们都知道图都是由结点以及结点之间的关联边组成的。直观上理解,绝对均匀的图应该是图中的所有结点的度都完全相同,这样每个结点都是同构的,也就是说从任何一个结点进行观察,得到的都是同样的结果。
形式化的描述应该是这样,对于图 \(G=(V, E)\) ,其中\(V\)是结点集合,\(E\)是边集合,记 \(|V|\) 为结点数, \(|E|\) 为边数,图的平均度为 \(D\) ,由于每条边为图贡献两个度,于是存在以下关系:
$
D = \frac{2\cdot|E|}{|V|}(公式1)
$
因此,根据前面对均匀概念的理解,对于绝对均匀图,任何一个节点的度数都满足:
$
d_v = D = \frac{2\cdot|E|}{|V|}(公式2)
$
二、简单讨论一下
明确了绝对均匀图的概念后,接下来就是如何生成的问题。由于
$
|E| = \frac{d_v\cdot|V|}{2}(公式3)
$
我们只需要控制结点数 \(|V|\) 和每个结点的度数 \(d_v\) 这两个变量即可。因此我们的目标就是生成任意结点数,且结点度数任意的绝对均匀图。
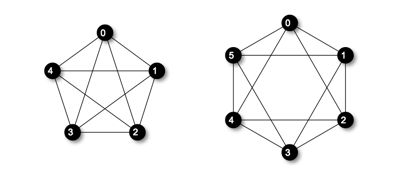
我们知道,完全图其实就是一种绝对均匀图,其所有节点的度数为 \(|V| - 1\) ,这已经是图中结点可以达到的最高度数了。相应的,空图(只有点,没有边)也是绝对均匀图,即所有节点的度数都为 \(0\),为最低度数。因此绝对均匀图的结点度数总是满足:
$
0\le d_v\lt|V|(公式4)
$
通过观察上面的公式2,我们还可以得出如下结论:
- 当结点数为奇数时,\(|V| = 2k - 1, k=1,2...\) , 由于 \(|E|\) 是整数,因此 \(d_v\) 必为偶数。
- 当结点数为偶数时,\(|V| = 2k, k=1,2...\) , \(d_v\) 没有限制,因为总有 \(|E| = d_v\cdot k\) 。
一言以蔽之,对于奇数点数的绝对均匀图,结点度数只能取 \([0, |V|)\) 之内的偶数。故而在图生成算法上需要对奇数点数图区分对待。
三、试一下递归?
那么如何构建绝对均匀图呢?首先比较容易想到的就是递归思想,递归的基本思路是:
- 构建问题最简单的规模实例,即递归的初值,或称为终止条件。
- 在最简单规模的实例基础上,通过增加问题规模,推测问题规模增大时,问题变化的规律。
- 继而推导在问题规模为\(n\)的时,构造问题规模为\(n+1\)的递归条件。这也就意味着,问题规模增大时得到的结果,总是蕴含,甚至包含上一级规模问题的结果。
上面讨论过,对于绝对均匀图,有两个变量影响图的规模:结点数 \(|V|\) 和结点度数 \(d_v\) 。因此分析时,要假定其中有一个不变量才比较好思考。
1. 结点度数不变,增大结点数
由于奇数结点数的图的结点度数不可能为奇数,因此我们保持结点度数为偶数不变,保证结点数从奇数到偶数再到奇数时,可以连续地推导问题变化规律。
这里取\(d_v = 2(0度不具备参考性,可作为边界条件考虑)\),令 \(|V| = 3, 4, 5, 6\),可以得到如下图实例。
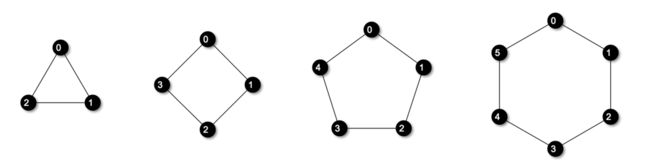
貌似按照环形图的思考方式,问题是可以递归的。每增加一个结点时,只需要选取一条边断开,然后连接到新的结点即可。
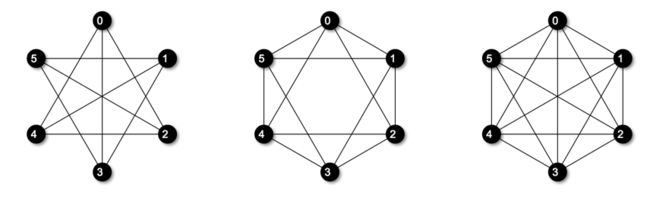
再考虑一下\(d_v = 4\)的情况,令 \(|V| = 5, 6\),可以得到如下图实例。
这种情况下,好像使用上述的递归扩展方式就不太容易了。那另外一种情况呢?
2. 结点数不变,增大结点度数
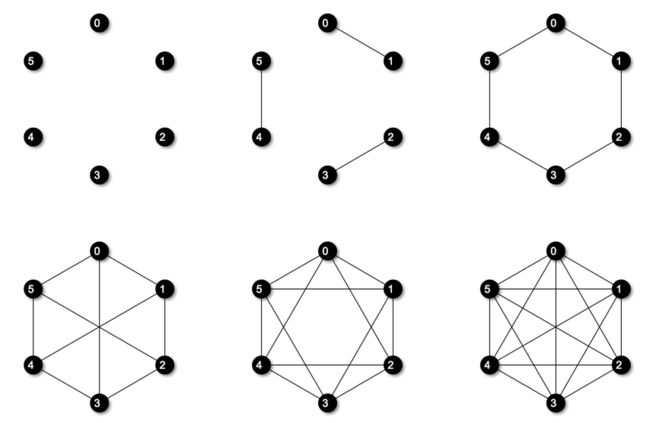
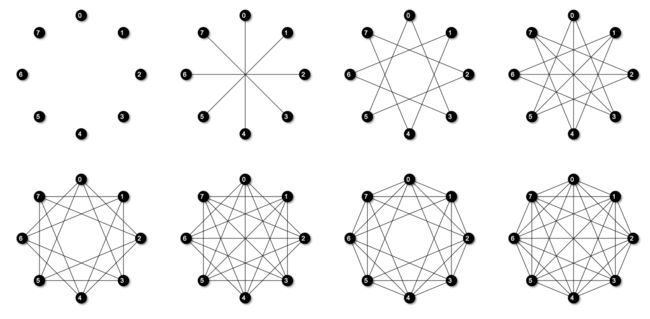
这里取 \(|V| = 6\),令 \(d_v = 0, 1, 2, 3, 4, 5, 6\),可以得到如下图实例。
可以看到,当度从\(3\)增长到\(4\)时,新规模问题的解并不包含上一级问题所有的解,而且每一级变化的规律并不稳定。
因此用上面的递归思想去分析绝对均匀图生成的问题可能并不方便,我们需要转换一下思路。
四、核心思想
回到第一节对绝对均匀图的概念描述:绝对均匀图的结点是同构的,满足各向同性。这就意味着我们可以从一个结点出发,去设法寻找它的关联节点,并且这种方式对任何一个结点都是相同的。
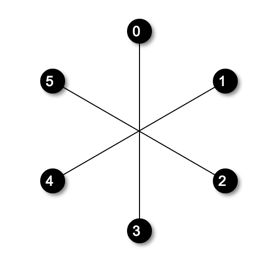
那么如何找到关联结点呢?考虑到绝对均匀图每个点都是同构的,因此绝对均匀图一定是中心对称的!假设这个虚拟的对称中心为\(O\),在\(d_v = 1\)的情况下,关联结点一定是当前结点的中心对称结点。
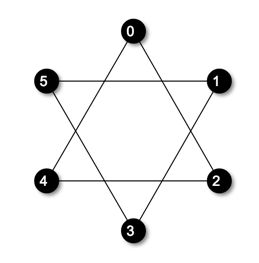
那在\(d_v = 2\)的情况下呢?
或许会有人好奇,这个\(d_v = 2\)的图怎么不是环呢?其实对于同样结点数和度数的绝对均匀图,图的结构可能不止一种。
按照中心对称思想依此类推,可以得到其他度的绝对均匀图。
因此,关联结点的寻找思路如下:
- 当\(d_v=2k(k=0, 1, 2...)\) 时,关联结点为当前结点的中心对称结点两侧的各\(k\)个结点。
- 当\(d_v = 2k + 1(k=0, 1, 2...)\) 时,关联结点为当前结点的中心对称结点加上中心对称结点两侧的各\(k\)个结点。
我们发现,前面讨论的不可行的递归方式主要是被环形图的思路干扰了。利用中心对称的关联结点寻找方式是也是可以递归的,不过使用循环实现可能更方便。
五、算法实现与测试
基于中心对称思想的绝对均匀图生成算法实现如下:
public boolean generate(int count, int degree) {
// 基本参数校验
if (!(count > 0 && degree >= 0 && degree < count)) {
System.err.println("Invalid arguments !");
return false;
}
// 检查奇数点图的度是否是偶数
if (count % 2 == 1 && degree % 2 != 0) {
System.err.println("Degree should be odd when vertices' count is even !");
return false;
}
// 生成点
System.out.println("Generating vertices:");
for (int index = 0; index < count; index++) {
System.out.println(index);
}
// 生成边
System.out.println("Generating edges:");
for (int index = 0; index < count; index++) {
// 对面的点
int opposite = (index + count / 2) % count;
// 点偶数,度奇数,链接中心对称结点
if (count % 2 == 0 && degree % 2 == 1) {
System.out.println(index + " -> " + opposite);
}
// 链接中心对称结点两侧的点
for (int i = (count + 1) % 2; i <= (degree - count % 2) / 2; i++) {
final int previous = (opposite - i + count) % count;
final int next = (opposite + i + count % 2) % count;
System.out.println(index + " -> " + previous);
System.out.println(index + " -> " + next);
}
}
return true;
}为了更直观的展示生成的绝对均匀图,可以借助vis.js库进行绘制。
具体实现方式可以访问github源码drawG,该项目实现了一个简单的图生成与绘制框架,可以方便定制和扩展图生成器和处理器。
最后,看一下使用该框架生成的绝对均匀图: