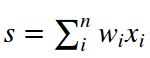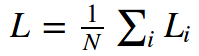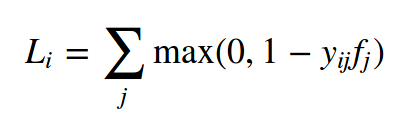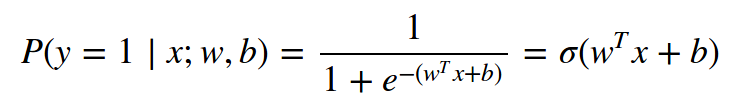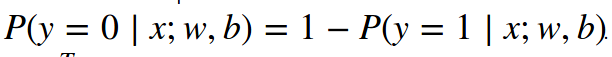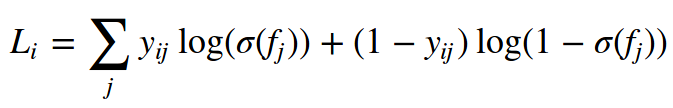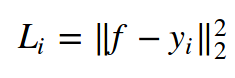说明:
本系列文章翻译斯坦福大学的课程:Convolutional Neural Networks for Visual Recognition的课程讲义 原文地址:http://cs231n.github.io/。 最好有Python基础(但不是必要的),Python的介绍见该课程的module0。
本节的code见地址:
https://github.com/anthony123/cs231n/tree/master/module1-6(working on)如果在code中发现bug或者有什么不清楚的地方,可以及时给我留言,因为code没有经过很严格的测试。
这节课的主要内容:
- 设置数据和模型
- 数据预处理
- 权重初始化
- 批量标准化
- 正则化(L2/L1/Maxnorm/Dropout)
- 损失函数
- 总结
设置数据和模型
在上一节课中,我们介绍了神经元的模型,它计算点积,然后计算一个非线性函数。神经网络将神经元组织成层级结构。总之,这种选择定义了一种新的分数函数,它 从我们在线性分类那节中的线性分类扩展而来。特别地, 神经网络计算一系列的线性映射,并和非线性操作交替出现。在这节中,我们会讨论数据预处理,权重初始化及损失函数的设计选择。
数据预处理
有三种常见的数据预处理的方法,我们假设数据矩阵X的大小是[NxD] (其中N是数据的数量, D是它们的维度)。
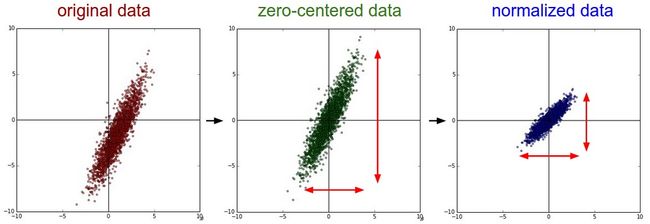
平均数减法 是一种非常常见的数据预处理方法,具体做法为减去所有特性的平均数。在几何上的解释,就是将所有的数据放在原点的周围,在numpy中,计算公式为X -= np.mean(X, axis = 0),以图像为例,可以对所有的像素都减去同一个值(比如,X -= np.mean(X)),也可以针对每一个通道单独处理。
标准化 是指将数据标准化,使得所有数据的变化范围都一样。有两种标准化的方法。一种是在数据中心化后,再除以它们的标准差。另一种方法是使得最小值和最大值为-1和+1。你使用标准化操作的理由是你认为不同的特征有不同的范围,但是它们对学习算法的重要性都是一样的。但是,对于图像数据而言,像素的范围都一样(0~255),所以这个预处理操作并不是必须的。
PCA和Whitening 是另外一种预处理的方法。首先将数据中心化,然后我们计算协方差矩阵,它告诉我们数据之间的相关性:
#假设输入数据矩阵X为[NxD]
X -= np.mean(X, axis = 0) #零中心化(重要)
cov = np.dot(x.T, x)/X.shape[0] #计算数据的协方差矩阵
协方差矩阵中(i,j)元素表示数据中第i个维度与第j个维度的协方差。特别地,这个矩阵的对角线为数据的方差。而且,协方差矩阵的对称和半正定的。我们可以通过下面的方法计算协方差矩阵的SVD分解:
U,S,V = np.linalg.svd(cov)
其中,U的列向量为特征向量,S是1维的奇异值向量(为特征值的平方)。为了对数据去相关化,我们把原始数据(已经零中心化)映射到特征坐标轴:
Xrot = np.dot(X,U)
我们可以注意到U的每一列都是正交标准向量,所以它们可以作为坐标向量。所以这个映射对应于数据X的一个旋转,以便所有的新轴都是特征向量。如果我们现在计算Xrot的特征向量,那么我们可以发现结果是一个对角线矩阵。np.lialg.svd的一个非常好的特性是它的返回值U的特征向量是按照特征值的大小排列的。我们使用这个特性,通过只使用最开始的几个特征向量来减少数据的维度,这也被称之为主成分分析(Principal Component Analysis PCA):
Xrot_reduced = np.dot(X,U[:,:100]) #xrot_reduced 为 [Nx100]
这个操作之后,我们把原始矩阵从[NxD]减少为[Nx100],只保存了100个方差最大的数据。在训练线性分类器或神经网络的过程中,使用PCA处理后的数据,可以获得很好的结果,并且可以节省大量的时间和空间。
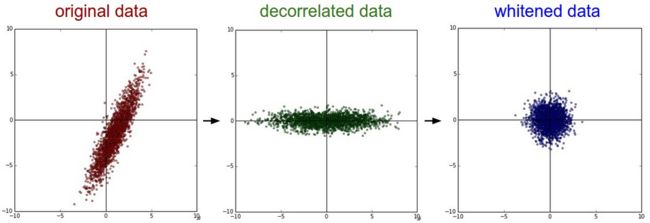
最后一个在实践中经常使用的操作是白化(whitening)。白化操作将特征坐标系下的数据除以特征值,来标准化它的返回。这种转变的几何解释就是,如果输入数据是一个多变量的高斯分布,那么白化后的数据便是以零为平均值,单位协方差矩阵为标准差的高斯分布。白化的代码为:
Xwhite = Xrot / np.sqrt(S + 1e-5)
警告:加大杂质
我们加入1e-5(或一个小的常量)来防止除零操作。这个操作的一个弱点是它们增加了数据中的杂质,它在数据的所有维度都增加了一个微小值。在实践中,它能够通过增加一个更大的平滑量(比如,将1e-5增加为一个更大的值)来缓解。
我们可以通过CIFAR-10图片来可视化这些操作。CIFAR-10的大小为50,000x3072,我们可以计算出[3072x3072]的协方差矩阵,并计算SVD分解(计算花费会比较大)。计算的特征向量看出去是什么样子的呢?下面的图片可以帮助你:
在实践中 我们介绍PCA/白化只是为了完整性,但是这些操作并不经常应用在卷积神经网络中。但是,零中心化非常重要,我们经常会看到将每个像素点做这种标准化。
常见的错误 预处理非常重要的一点是任何预处理(比如 计算数据的平均值)必须在测试数据上计算,然后应用到验证/测试集中。直接计算每张图片的平均值,然后将每张图片减去这个平均值的做法是错误的。平均值必须在训练集上测试,然后在所有的图片中减去这个值。
权重初始化
我们已经知道如何构造一个神经网络架构,及如何对数据进行预处理。在开始训练网络之前,我们必须要初始化这些参数。
错误的做法:零初始化
我们先了解什么做法是错误的。我们并不知道每个权重的最终值是多少,但是我们可以假设其中有一半的权重是正数,一般的权重为负数。一个听起来不错的初始化方法便是设置所有的权重为零,因为至少我们对平均值的猜测非常好。但是实践表明,这个做法是错误的,因为如果每个神经元的输出都一样,那么它们在反向传播过程中都计算出相同的梯度,从而使得参数更新都一样。也就是说,如果权重都初始化为相同的话,那么所有的神经元都是对称的。
小的随机数字
我们还是需要非常小的随机数字,但是就像我们讨论的那样,不能都等于零。一个解决方案是,把所有的权重都初始化为小的数字,从而可以打破这种对称性。其思想为:所有的神经元都是随机和不同的,所以不同的神经元有不同的更新,并最后将这些神经元整合成一个网络。一个可能的实现方式为:W = 0.01*np.random.randn(D,H),其中randn产生的数字为以零为平均值,单位标准差的高斯分布。使用这种方式,每个神经元的权重矩阵都从多维度高斯分布中随机初始化。所以神经元在输入空间内指向不同的方向。我们也可以从一个分布中随机生成数据,但是在实践中,它对最后的效果并没有很大的影响。
警告 更小的数字不一定会产生更好的结果。比如,拥有小权重初始值的神经网络在反向传播过程中,会生成比较小的梯度(因为梯度值和权重值成正比)。这回导致梯度信号减少。所以,对于一个深度的网络,这是需要考虑的一个因素。
使用1/sqrt(n)校准方差 上面建议的一个问题在于随机初始化神经元的输出分布方差会随着输入规模的增加而变大。我们可以通过除以输入数目的平方根来标准化每个神经元的输出方差。这可以确保神经网络中的所有神经元输出有相同的分布,而且实践证明,它也会提高聚合的速率。
我们可以推导一下分数函数的方差。我们考虑內积
,我们可以计算s的方差
在前两步中,我们使用了方差的特性。在第三步中,我们假设输入和权重的平均值为零。所以,E[xi] = e[wi] = 0。注意:有的时候并不能做这种假设,对于ReLU,我们会有一个正的平均值。在最后一步中,我们假设所有的Wi和Xi的分布都一样。从这个推导我们可以看出,如果我们想要s和输入x的分布一样,那么在初始化过程中,我们需要保证权重的方差为1/n。因为Var(aX) = a^2Var(X),所以a=1/sqrt(n)。所以w的初始化为w=np.random.randn(n)/sqrt(n)。
在Glorot的论文 Understanding the difficult of training deep feedforward neural networks 有过类似地分析。在这篇论文中, 作者推荐另外一种初始化的方法。一篇更近的关于这个主题的论文是Delving Deep into Rectifiers: Suepassing Human-Level Performance on ImageNet Classification. 在这篇论文中,推导了一种针对于ReLu神经元的初始化。最终得到的结论是w应该初始化为 w = np.random.randn(n)*sqrt(2.0/n)。
稀疏初始化 另外一种解决这种非校准方差问题的方法是先把所有的权重矩阵都初始化为0, 但是为了破坏对称性,每个神经元都随机和下一层的固定的神经元连接。一般,神经元为个数10个。
初始化偏置值 我们通常将偏置值初始化为零。因为在权重随机化过程中已经破坏了对称性。对于ReLU,有些人喜欢使用0.01初始化偏置值。因为这保证了所有的ReLU单元在最开始就能激活,并能够获得并传播梯度。但是,它是否能够提供一个稳定的提高,并不明确(实际上,一些结果表明,它使得最终的效果变得更差)。所以人们经常用0来初始化偏置值。
在实践中, 对于ReLU单元的神经元,我们经常使用的初始化公式为 w=np.random.randn(n)*sqrt(2.0/n)。
批量标准化 Szegedy 最近提出了一种新的技术叫批量标准化(Batch Normaization) ,它通过显式地使得通过网络的激活值在训练的开始就服从正态分布。重要的是这是可能的,因为标准化是一个简单的微分操作。在代码实现中,我们经常通过插入一个批量标准化层(BatchNorm layer)来实现。批量标准化层通常插入在全连接层(或者卷积层)后面,在非线性层前面。我们不展开讲这种技术,因为它在这篇论文中讲的很清楚了。在神经网络中使用这个技术,已经是一个非常常见的做法了。在实践中,使用批量标准化的神经网络对不好的初始化值具有更好的鲁棒性。除此之外,批量标准化还可以解释为对每一层的网络中数据做预处理,然后以可微分的形式连接成一个网络。
正则化
下面讲解几种常见的防止过拟合的方法:
L2 正则化 是最常见的正则化方法。它可以直接惩罚目标函数中所有参数的平方量。也就是说,对于神经网络的每个权重w,我们增加一项 1/2λ(w^2),其中λ是正则强度。在λ前面我们通常增加1/2,是为了使得这一项的导数为λW,而不是2λW。L2正则项可以惩罚高的权重值,并且更喜欢分散的权值向量。就像我们在线性分类那一节讲的那样,由于权重和输入有点积乘法,使得整个网络能够使用所有的输入而不是部分输入。最后,注意到在梯度下降参数更新过程中,使用L2正则化会最终意味着每个权重都线性地衰减: W += -λW,并不断地趋近于零。
L1正则化 是另一种常见的正则化方法。对于每个权重w,我们增加λ|w|到目标函数中。我们将L1和L2结合起来也是可能的:
(这称之为弹性网络正则化 Elastic net regularization)。L1正则化的特性是它使得在优化过程中权重向量变得更加稀疏(非常接近于零)。换句话说,L1正则化的神经元只使用其中最重要的输入子集,所以可以抵抗杂质输入。而L2正则化的最终权重向量通常是分散的,小的数字。在实践中,如果你不考虑显式特征的选择,那么L2正则项会比L1正则项的效果更好。
最大正则限制
另外一种正则方法是对每个神经元的权重向量规定一个绝对上限,使用映射后的梯度下降来强制限制。在实践中,首先正常更新参数,然后通过设定一个c值,使得||w||< c。有些实验表明这能够提高效果。这种方法的一个好的特性当学习速率设置太高,但是网络不会“爆炸”,因为更新后的值永远有上限。
Dropout 是由Srivastava在论文Dropout: A simple Way to Prevent Neural Networks from Overfitting 中介绍的一种非常有效,简单的正则方法。在训练过程中,Dropout只以p(超参数)的概率激活一个神经元。
"""Vanilla Dropout: 一种不推荐的实现方法"""
p = 0.5
def train_step(X):
""" X contains the data"""
#三层神经网络的前向传播
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = np.random.rand(*H1.shape) < p #第一个dropout遮蔽图
H1 *= U1 #drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) < p #第二个Dropout遮蔽图
H2 *= U2 #drop
out = np.dot(W3, H2) + b3
#反向传播,计算梯度...
#进行参数更新...
def predict(X):
H1 = np.maximum(0, np.dot(W1,X) + b1) * p
H2 = np.maximum(0, np.dot(W2,H1) + b2) * p
out = np.dot(W3, H2) + b3
在上面的代码中,在train_step函数中,我们进行了两次Dropout操作:在第一个隐藏层和第二个隐藏层。我们也可以直接在输入层进行Dropout操作,反向传播操作保持不变,但是我们必须要考虑到生成的遮蔽图U1和U2。
注意: 我们在predict函数中不再丢掉神经元,但是我们将两个隐藏层的参数的大小都缩小了p。这非常重要,因为在测试阶段,神经元能看到所有的输入,而我们希望在测试阶段,神经元的输入与训练阶段神经元的输出一样。比如,如果p=0.5, 为了使得测试神经元的输出与训练神经元的输出一样,那么在测试阶段,所有的神经元都必须要减半。假设一个神经元的输出为x, 那么加入Dropout之后,输出为px+(1-p)0 = px。所以,在测试阶段,我们必须将输出结果乘以参数p,才能使得最后的输出结果为px。
这种方法的一个不好的地方在于我们必须在测试阶段乘以参数p。因为测试阶段的时间花费很宝贵。所以我们经常使用inverted dropout 。它在训练阶段就将参数变化为1/p,而在测试阶段不需要做任何其他的处理。代码如下:
"""Inverted Dropout: 推荐的实践方法.
在训练阶段进行drop和scale操作,而在测试阶段不做任何事情
"""
p = 0.5
def train_step(X):
#三层神经网络的前向传导
H1 = np.maximun(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape)在Dropout概念介绍之后,有大量的研究试图理解它的效果来源及它与其他正则技术的关系。有兴趣的读者可以阅读以下论文:
- Dropout paper by Srivastava et al. 2014
- Dropout Training as Adaptive Regularization
前向传导中的杂质
Dropout引入了神经网络前向传播的随机行为。在测试阶段,杂质分析地(在Dropout例子中,是乘以p)或数值地(先通过取样,使用不同的随机决定来进行几次前向传导,最后取它们的平均)边缘化。一个在这方面的研究包括DropConnect, 其中在前向传播过程中,随机取一些权重,并把它们设为零。顺便提一下,在卷积神经网络中,也利用了这种方法,比如:随机池化(stochastic pooling), 分数池化(factional pooling), 数据扩大(data augmentation)。在后面我们会详细讲解这些内容。
偏置正则化
在线性分类这一节中我们提过,通常我们不正则化偏置参数,因为它们并不和数据进行乘法操作。所以也无法在最后的目标函数中对数据维度有影响。然而,在实践中,正则化偏置量很少会导致更差的效果。这很可能是因为相对于权重参数的个数来说,偏置量的参数个数非常少,所以分类器能够通过改变自己而达到更好的结果。
每层的正则化
针对每一层,使用不同的正则项的做法并不常见。关于这方面的主题的研究相对来说比较少。
在实践中, 我们通常使用一个全局的L2正则项(这个值由交叉验证得出)。我们通过将它与Dropout(在所有层的最后使用)结合起来使用也非常常见。p=0.5是常用的默认值,但是也可以根据验证集来调整。
损失函数
我们已经讨论了目标函数中正则损失部分,它可以看成是惩罚模型的复杂性。目标函数的第二部分是数据损失,它在监督学习问题中测量预测和真实标签的契合性。数据损失计算每个单独例子的平均数据损失。计算公式如下:
其中N是训练数据的个数。在实践中,我们可能需要解决几种类型的问题:
分类 问题我们在之前已经讨论过。我们假设我们有一个数据集,而且每个数据集中的图片都有一个标签。两种最常用的花费函数之一是SVM
有些人报告称平方的铰链损失能取得更好的效果。第二个常见的选择是Softmax分类器,它使用交叉熵损失
大数量的类别
当标签的数据集非常大(比如英语词典的单词,或者ImageNet包含22,000个类别),我们需要使用层级Softmax(Hierarchical Softmax),层级Softmax将类别组织成一棵树。那么每个标签可以表示为沿着一棵树的路径。Softmax分类器就训练树的每个节点来分辨左枝和右枝。树的结构非常影响最终的效果,并且树的结构一般都取决于问题的类别。
特征分类器
上面两种损失都假设只有一个正确答案yi,如果yi是一个向量,其中每个值表示包含或者不包含某个特征,而且每个特征都不是互斥的。比如,在Instagram上的图片都有很多标签。解决这个问题的一个可行的方法是对应每张图片,都建立一个特性向量。比如,一个二元分类器的公式如下:
其中 Li是所有类别j的总和。yij要么是+1,要么是-1,取决于第i个图片是否具有第j种特性。当被预测成这个类别是,那么分数向量fj就为正,否则就为负。从上面的例子我们也可以看出,如果正样例的分数大于+1, 或者当负样例大于-1.
另外一种计算这种损失的方法是对每个特征单独训练一个逻辑回归分类器。一个二元逻辑回归分类器只有两个种类(0,1),计算分到种类1的概率为:
因为种类1和种类0之和为1。种类0的概率为:
所以,一个样例
或者 Wx+b > 0, 那么它就被归类于正样本(y=1)。损失函数然后最大化这个概率的log形式。你可以说服自己这种操作可以简化为如下公式:
其中yij的取值是1或0。σ(.)是sigmoid函数。这个表达式咋看起来很吓人,但是梯度f却非常简单。∂Li/∂fj=yij−σ(fj)∂Li/∂fj=yij−σ(fj)。
回归 可以预测实数数量的任务。比如房子的价格,或者在图片中某种纹理的长度。对于这种类型的任务,我们通常计算预测的数量与真实的答案之间的差别,然后计算L2平方差距或者L1差别。L2平方差距的计算公式如下:
L2平方的理由在于计算简单,而且还能保持单调性不变。L1的计算公式如下:
如果维度的个数大于1,则求所有维度的和。我们现在只看第i个样例的第j个维度,将预测与真实之间的差异表示为δij, 那么这个维度的梯度要么是δij(L2 norm),要么是sign(δij)。也就是说,分数梯度要么正比于差异,或者为差异的符号。
注意: L2损失比更稳定的损失比如Softmax更难优化。直觉上理解,网络需要一个特别的特性来对每一个输入产生一个正确结果。但是对Softmax,却不是这样。其中,每个分数的准确值不是最重要的。只要它们的大小合适就行。而且,L2损失具有更少的鲁棒性因为杂质能够导致更大的梯度。当遇到回归问题的时候, 我们首先考虑是否将输出量化为等间距的值是否是不够的。比如,我们对意见产品进行评价,我们可以使用1~5来进行评分,而不是使用回归损失。分类还有一个附加的好处,就是你可以看到回归输出的分布,而不是一个单独的数字。如果你确定分类是不合适的,那么也可以使用L2,但是必须要小心:比如: L2更加脆弱,并且应用Dropout(特别是在L2损失之前)并不是一个很好的想法。
当遇到回归问题,首先考虑这是否是必须的。我们应该首先考虑将你的输出等间距化,并对它们使用分类。
结构化预测 结构化损失指的是标签可以变成随意的结构,比如图,树或者其他复杂的结构。通常我们也假设结构的空间非常大,而且不可数。结构化SVM背后的想法是要求正确结构yi和最高分数的错误答案的间距。解决这个问题的通常不使用梯度下降来解一个简单的非限制的优化问题。我们通常会有一个简单的假设,从而设计一个特别地求解方法。具体的细节已经超过了本课程。
总结
- 推荐的预处理数据方法是使得数据的平均值为0,而且将其范围标准化为[-1,1]。
- 在初始化权重时,我们从标准差为sqrt(2/n)的高斯分布中选取数值,其中n为神经元输入的个数。用numpy实现的代码为 w = np.random.randn(n)*sqrt(2.0/n)
- 使用L2和Dropout(反向版本)
- 使用批量标准化
- 我们讨论了在实践中我们会遇到的不同的任务,以及每个任务的损失函数。
我们现在已经预处理了数据,初始化了模型,下一节我们会讨论学习过程及它的动态性。