DenseNet 论文阅读笔记

Densely Connected Convolutional Networks

原文链接

摘要

研究表明，如果卷积网络在接近输入和接近输出地层之间包含较短地连接，那么，该网络可以显著地加深，变得更精确并且能够更有效地训练。该论文基于这个观察提出了以前馈地方式将每个层与其它层连接地密集卷积网络(DenseNet)

如上所述，所提出的网络架构中，两个层之间都有直接的连接，因此该网络的直接连接个数为\(\frac{L(L+1)}{2}\)。对于每一层，使用前面所有层的特征映射作为输入，并且使用其自身的特征映射作为所有后续层的输入

DenseNet的优点: 缓解了消失梯度问题，加强了特征传播，鼓励特征重用，并大大减少了参数的数量

引言

当CNNs增加深度的时候，就会出现一个紧要的问题：当输入或者梯度的信息通过很多层之后，它可能会消失或过度膨胀。在本研究中提出的架构为了确保网络层之间的最大信息流，将所有层直接彼此连接。为了保持前馈特性，每个层从前面的所有层获得额外的输入，并将自己的特征映射传递给后面的所有层

示例（一个5层的密集块）

该架构与ResNet相比，在将特性传递到层之前，没有通过求和来组合特性，而是通过连接它们的方式来组合特性。因此第x层（输入层不算在内）将有x个输入，这些输入是之前所有层提取出的特征信息。因为它的密集连接特性，研究人员将其称为Dense Convolutional Network (DenseNet)

因为不需要重新学习冗余特征图，这种密集连接模式相对于传统的卷积网络只需要更少的参数。传统的前馈体系结构可以看作是具有一种状态的算法，这种状态从一个层传递到另一个层。每个层从其前一层读取状态并将其写入后续层。它改变状态，但也传递需要保留的信息。研究提出的密集网络体系结构明确区分了添加到网络的信息和保留的信息。密集网层非常窄（例如，每层12个过滤器），仅向网络的“集体知识”添加一小组特征映射，并且保持其余特征映射不变，并且最终分类器基于网络中的所有特征映射做出决策
想法：能不能先学习图像中能够区别分类的地方，然后将该图像信息提取进行学习

除了参数更少，另一个DenseNets的优点是改进了整个网络的信息流和梯度，这使得它们易于训练。每个层直接访问来自损失函数和原始输入信号的梯度，带来了隐式深度监控。这使得训练深层网络变得更简单。此外，研究人员观察到密集连接具有规则化效果，这减少了对训练集较小的任务的过拟合

相关工作

Highway 网络是第一批提供了有效训练具有100多个层的端到端网络的架构之一。利用旁路和门控单元，可以毫无困难地优化具有数百层的Highway网络。旁路路径被认为是简化这些深层网络训练的关键因素。ResNets进一步支持这一点，其中纯identity映射用作旁路路径。ResNet表明随机深度是训练成功的一种方法，随机深度通过在训练过程中随机丢弃层来改进深度残差网络的训练。这表明，并非所有层都是需要的，并强调在深（剩余）网络中存在大量的冗余，该研究深受此想法的启发。使网络更深（例如，在跳过连接的帮助下）的正交方法是增加网络宽度，如GoogLeNet

DenseNets没有从极深或极宽的体系结构中汲取表示能力，而是通过特征重用来开发网络的潜力，从而产生易于训练和高参数效率的浓缩模型。由不同层学习的连接特征图增加了后续层输入的变化，提高了效率。这构成了DenseNets和ResNets之间的主要区别

DenseNets

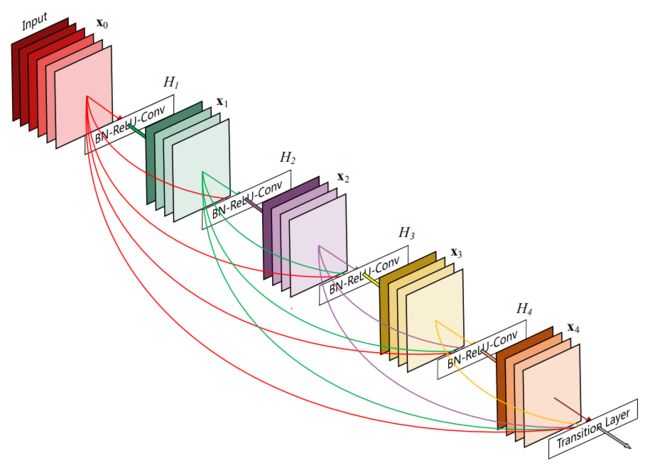
对于一个卷积网络，假设输入图像\(x_0\)。该网络包含 \(L\) 层，每一层都实现了一个非线性变换\(H_i(.)\)，其中\(i\)表示第\(i\)层。\(H_i(.)\)可以是一个组合操作，如：BN，ReLU，Pooling或者Conv。将第i层的输出记作\(x_i\)

Dense connectivity

为了进一步改善层之间的信息流，研究者提出了不同的连接模式：引入从任何层到所有后续层的直接连接

结果，第 \(i\) 层得到了之前所有层的特征映射\(x_0, x_1, ... ,x_{i-1}\)作为输入
\[ x_i = H_i([x_0, x_1, ... , x_{i-1}]) \]
\([x_0, x_1, ... , x_{i-1}]\)表示特征映射的级联

Composite function

定义\(H_i(.)\)为一个三个连续操作的组合函数：BN, ReLU, 3*3卷积(Conv)

Pooling Layers

当特征映射的大小改变时，上式中使用的连接操作是不可行的。然而，卷积网络的一个重要部分是改变特征映射大小的下采样层。为了简化架构中的下采样，我们将网络划分为多个紧密连接的密集块；将块之间的层称为过渡层，它执行卷积和合并。实验中使用的过渡层由批量归一化层和1×1卷积层以及2×2平均池化层组成

3个dense blocks组成的一个深度DenseNet

Growth rate

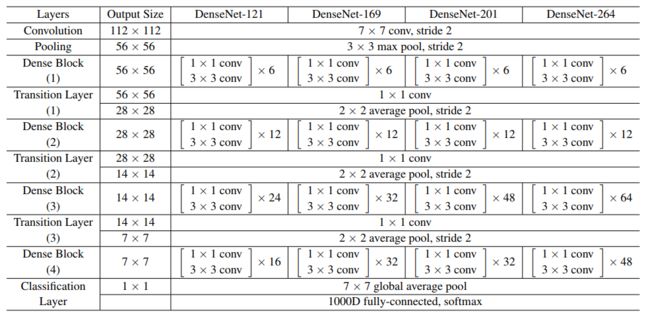
当每个 \(H_i\) 都产生 \(k\) 个特征映射时，它表示第 \(i\) 层有 \(k_0 + k * (i - 1)\)个输入特征映射， \(k_0\) 表示输入层的通道数。DenseNet与已存在的架构的不同在于DenseNet可以有很窄的层，eg: \(k = 12\)。将超参数 \(k\) 称为网络的 growth rate。下表将显示一个相对较小的growth rate就能够获得很好的结果

\(k = 32\) conv层表示BN-ReLU-Conv

对此的一种解释是每个层可以访问其块中的所有前面的特征映射，因此可以访问网络的“集体知识”。人们可以将特征映射看作网络的全局状态。每个层将自己的 \(k\) 个特征映射添加到这个状态。增长速度控制着每一层新信息对全局状态的贡献。全局状态一旦写入，就可以从网络内的任何地方访问，并且与传统网络体系结构不同，不需要逐层复制它

Bottleneck layers

虽然每一层只产生k个输出特征映射，但它通常具有更多的输入。有文章中指出，在每3×3卷积之前可以引入1×1卷积作为瓶颈层，以减少输入特征映射的数量，从而提高计算效率。研究发现这种设计对于DenseNet特别有效，并将具有瓶颈层的网络称为DenseNet-B，即具有BN-ReLU-Conv(1×1)-BN-ReLU-Conv(3×3)版本的\(H_i\)

Compression

为了进一步提高模型的紧凑性，可以减少过渡层上的特征映射的数量。如果一个dense block包含 m 个特征映射，可以让紧跟着的变化层生成 \(\lfloor \theta_m \rfloor\)个输出特征映射， $ 0 < \theta \leq 1$作为压缩因子。当 \(\theta = 1\) 时，跨转换层的特征映射的数量保持不变

Discussion

从表面上看，DenseNets非常类似于ResNets，区别仅在于计算 \(H_i(.)\)时使用的是串联而不是求和。然而，这个看似很小的修改的含义导致了两个网络体系结构的实质上不同的行为

模型紧凑性

作为输入级联的直接结果，任何DenseNet层学习的特征映射都可以被所有后续层访问。这鼓励在整个网络中的特性重用，并导致更紧凑的模型

隐性深度监督

对于提高密集卷积网络精度的一种解释是，各个层通过较短的连接从损失函数接收额外的监督。可以将DenseNets解释为执行“深度监管”。深层监控的好处以前在深层监控网络中已经显示出来，深层监控网络具有附加到每个隐藏层的分类器，从而强制中间层学习区分特征

DenseNets以隐式的方式执行类似的深层监控：网络顶部的单个分类器通过最多两个或三个过渡层对所有层提供直接监控。然而，由于所有层之间共享相同的损耗函数，因此DenseNets的损耗函数和梯度基本上不那么复杂

随机与确定性连接

在随机深度，残差网络中的层被随机丢弃，从而在周围层之间建立直接连接。由于池化层从未被丢弃，因此网络产生了与DenseNet类似的连接模式：如果所有中间层被随机丢弃，那么在同一池化层之间的任何两层被直接连接的概率都很小。虽然方法最终完全不同，但随机深度的密集网解释可能为该正则化器的成功提供见解

特征复用

通过设计，DenseNets允许层访问来自其所有先前层（尽管有时通过转换层）的特征图。通过实验可以得出以下结果

1. 所有层将权重分散在同一块内的许多输入上。这表明，由非常早期的层提取的特征实际上被整个同一dense block的深层直接使用
   
2. 过渡层的权重还将它们的权重分布在前面密集块内的所有层上，指示信息从DenseNet的第一层到最后一层通过很少的间接流动
   
3. 第二密集块和第三密集块内的层始终向过渡层的输出(三角形的顶行)分配最小的权重，指示过渡层输出许多冗余特征(平均权重较低)
   
4. 尽管最终分类层也使用整个密集块的权重，但是似乎存在对最终特征映射的集中，这表明可能在网络后期产生一些更高级的特征

结论

提出了一种新的卷积网络结构，并将其称之为稠密卷积网络（DenseNet）。它引入了具有相同特征映射大小的任意两个层之间的直接连接。我们发现，DenseNets可以自然地扩展到数百个层，而没有表现出优化困难。在实验中，DenseNets趋向于随着参数数量的增加，在精度上产生一致的提高，而没有任何性能下降或过拟合的迹象