写在前面
这个东西其实是有价值的东西。因为在软体模拟、数学方程可视化、流体模拟、数据可视化等等方面都有其用武之地。
如水的模拟:
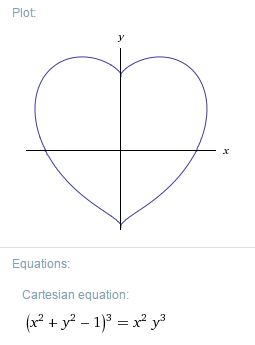
心形函数方程转图像
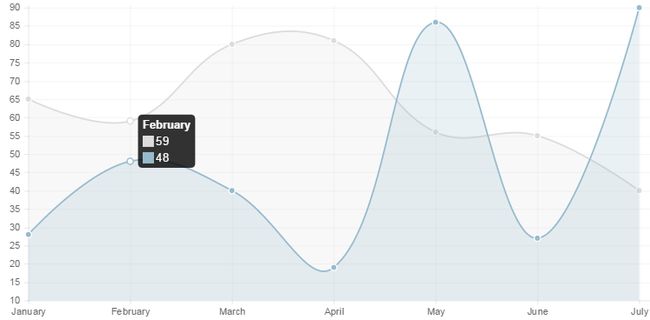
线性报表
其原理都是通过三次贝塞尔曲线将有限个数的点平滑化。
问题建模
已知若干个点,绘制出该点连接的曲线。
这里实验平台使用浏览器环境,即Canvas相关API以及javascript语言。
这里canvas的上下文对象拥有了bezierCurveTo方法,故免去了自己实现bezierCurveTo的一些事情。
context.bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y);实现图解
实现目标
代码
Vector2,一般用来表示向量,但有的时候也用来当作点来进行一计算。
var Vector2 = function(x, y) {
this.x = x;
this.y = y;
}
Vector2.prototype = {
"length": function () {
return Math.sqrt(this.x * this.x + this.y * this.y);
},
"normalize": function () {
var inv = 1 / this.length();
return new Vector2(this.x * inv, this.y * inv);
},
"add": function (v) {
return new Vector2(this.x + v.x, this.y + v.y);
},
"multiply": function (f) {
return new Vector2(this.x * f, this.y * f);
},
"dot": function (v) {
return this.x * v.x + this.y * v.y;
},
"angle": function (v) {
return Math.acos(this.dot(v) / (this.length() *v.length())) * 180 / Math.PI;
}
}其中
length求向量长度
normalize转单位向量
add向量叠加
multiply向量翻倍
dot内积
angle方法用来求两个向量的夹角
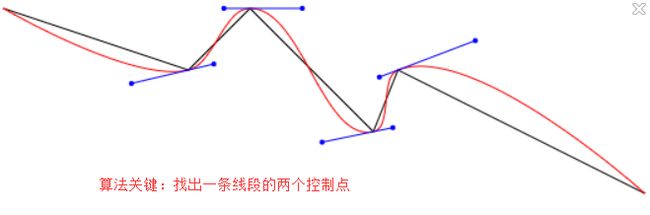
核心方法,根据path上的点,求出所有贝塞尔曲线控制点。
function getControlPoint(path) {
var rt = 0.3;
var i = 0, count = path.length - 2;
var arr = [];
for (; i < count; i++) {
var a = path[i], b = path[i + 1], c = path[i + 2];
var v1 = new Vector2(a.x - b.x, a.y - b.y);
var v2 = new Vector2(c.x - b.x, c.y - b.y);
var v1Len = v1.length(), v2Len = v2.length();
var centerV = v1.normalize().add(v2.normalize()).normalize();
var ncp1 = new Vector2(centerV.y, centerV.x * -1);
var ncp2 = new Vector2(centerV.y * -1, centerV.x);
if (ncp1.angle(v1) < 90) {
var p1 = ncp1.multiply(v1Len * rt).add(b);
var p2 = ncp2.multiply(v2Len * rt).add(b);
arr.push(p1, p2)
} else {
var p1 = ncp1.multiply(v2Len * rt).add(b);
var p2 = ncp2.multiply(v1Len * rt).add(b);
arr.push(p2, p1)
}
}
return arr;
}Demo
点我点我