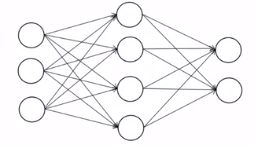
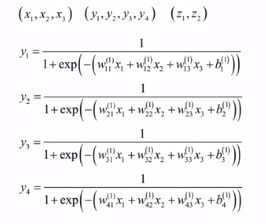全连接神经网络:也叫多层感知器模型
BP不是神经网络,是训练神经网络的一种方法。
人脑大约800亿个神经元组成,这些神经元由突触与其他神经元相互连接,交换电信号和化学信号,大脑通过神经元之间的协作完成各种功能。神经元之间的连接关系是通过进化、生长发育和后天刺激形成的。
人工神经网络:
受动物神经系统的启发,是一种放生的方法,但只是简单的模仿,是感知器模型、logistic回归的进一步发展。在神经网络还没出来之前,是机器学习和感知器模型。
神经元的原理:f(wTx+b),加权w、b和激活f
输入值、连接权重、输出值、激活函数
sigmoid函数:f(x)=1/(1+e-x),定义域、值域、单调性,导数为f(x)*(1-f(x)),即不需要知道一点的x值,只需知道该点的y(f(x))值就可以知道该点的导数值。
神经网络结构:
多层前馈神经网络:也称为多层感知器模型MLP、全连接神经网络
是一个分层结构(输入层,隐含层可以多个,输出层),每一层有多个神经元
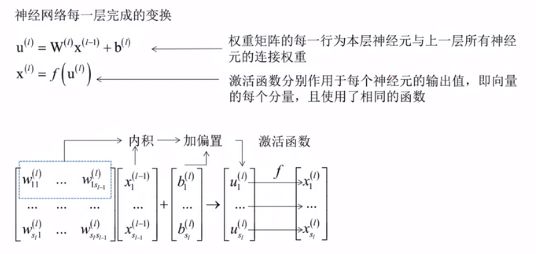
权重矩阵:每一行表示本层一个神经元和前一层所有神经元的连接权重,如果前一层有n个神经元,本层m个神经元,那么该矩阵为m*n的矩阵
正向传播算法:
神经网络实现的是向量到向量的映射 Rn-->Rm,本质上是一个多层的复合函数,通过调整权重和偏置项实现不同的映射,权重和偏置项的值通过训练得到。
神经网络过程:权重矩阵w和偏置向量b是通过训练算法训练出来的,训练出来以后,利用正向传播算法,根据输入值预测出一个输出值,输出值就是想要的分类结果或回归结果。
输入层的层数:输入特征向量的维数
怎么用于实际问题:
分类问题:输入值为特征向量或原始数据,输出值为one-hot编码。分类结果为输出层神经元的最大值。
回归问题:输出值为回归函数值。直接是输出层的值。
反向传播算法:简称BP神经网络,用来训练神经网络,求出权重w和偏置项b
通过反向传播算法和梯度下降法使损失函数L最小化
解决神经网络参数求导问题,源自微积分中多元函数求导的链式法则,与梯度下降法配合,完成网络的训练。
激活函数作用:使神经网络的复合函数是非线性的,如果去掉激活函数,不管神经网络是多少层,都是线性函数。
训练的目标是最小化训练样本的预测误差,以均方误差为例(也叫欧氏距离):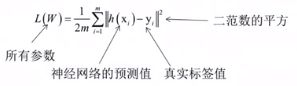
如果对所有参数的梯度值已经计算出来,则可以用梯度下降法更新:![]()
每层都有权重矩阵与偏置向量,如何计算损失函数对它们的导数值呢?就是反向传播要做的事情。