用Python解决数据结构与算法问题(一):Python基础
python学习之路 - 从入门到精通到大师
文章目录
- [python学习之路 - 从入门到精通到大师](https://blog.csdn.net/TeFuirnever/article/details/90017382)
- 一、你好世界
- 二、数据入门
- 2.1、列表
- 2.2、字符串
- 2.3、元组
- 2.4、集合
- 2.5、字典
- 三、输入和输出
- 四、控制结构
- 五、处理异常
- 六、定义函数
- 七、面向对象编程:定义类
- 7.1、一个分数类
- 7.2、逻辑门和电路
- 八、总结
- 参考文章
一、你好世界
来通过一些详细的例子回顾一下 Python 编程语言。 这里的目标是重新认识下 Python 语言,并强化一些将成为后面重点的概念。但是如果你是Python新手的话,或者你需要有关提出的任何主题的更多信息,建议参考 Python语言参考或 Python教程。
Python是一种现代的,易于学习的面向对象的编程语言。 它具有一组强大的内置数据类型和易于使用的控件结构。 由于是解释型语言,因此通过简单地查看和描述交互式会话,更容易进行检查。所以好多人会和你说推荐你使用 anaconda 的,比如:深度学习入门笔记(五):神经网络的编程基础。
在 jupyter notebook 中 >>> 是提示输入语句,然后计算你提供的Python语句。 例如:
>>> print("Hello,World")
Hello,World
>>> print("\n".join("Hello World"))
二、数据入门
因为Python是支持面向对象的编程范式,这意味着Python认为在解决问题的过程中的重点是 数据。在任何面向对象的编程语言中,类都是被定义用来描述 数据的外观(状态) 和 数据能做什么(行为)。因为类的用户只看数据项的状态和行为,所以类类似于抽象的数据类型。数据项在面向对象的范式中称为 对象,对象是类的实例。
Python有:
- 两个主要的内置数字类,分别是
int(整型数据类型)和float(浮点数据类型)。 - 标准的算术运算,
+,-,*,/,和**(取幂),可以用括号强制操作的顺序来规避正常的操作符优先级。 - 其他很有用的操作是
余数(模组)操作符%、和整数除法//。注意,当两个整数相除,结果是一个浮点数。整数除法运算符通过截断所有小数部分来返回商的整数部分。 - 布尔数据类型,作为Python bool类的实现,在表示真值时非常有用。
布尔数据
在标准的布尔操作中,and、or、not,布尔类型的状态值可能是 True 和 False。
>>> True
True
>>> False
False
>>> False or True
True
>>> not (False or True)
False
>>> True and True
True
布尔数据对象也被用作比较运算符的结果,例如相等(==)和大于(>)。
关系运算符和逻辑运算符
此外,关系运算符和逻辑运算符可以组合在一起形成复杂的逻辑问题。下表展示了关系和逻辑运算符:

标识符
标识符在编程语言中作为名称使用。在Python中,标识符以字母或下划线(_)开头,大小写敏感,并且可以是任意长度的。请记住,使用表示含义的名称。
赋值语句
在赋值语句的左边第一次使用一个名称时,就会产生一个Python变量。赋值语句提供了一种将名称与值关联起来的方法。该变量将持有对一块数据的引用而不是数据本身。思考以下会话:
>>> theSum = 0
>>> theSum
0
>>> theSum = theSum + 1
>>> theSum
1
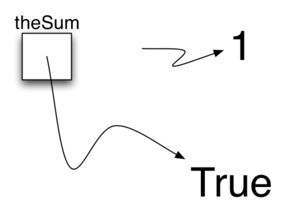
>>> theSum = True
>>> theSum
True
赋值语句 theSum = 0 创建一个变量称为 theSum 并让它持有对数据对象0的引用。通常,会对赋值语句的右侧进行求值,并将对结果数据对象的引用赋值给左侧的名称。如果数据的类型发生变化,变成布尔值 True,那么变量的类型也如此,theSum 现在变成布尔型。即相同的变量可以引用许多不同类型的数据。

除了数字和布尔类之外,Python还有许多非常强大的内置集合类。
- 列表、字符串和元组是有序集合。
- 集合和字典是无序的集合。
2.1、列表
列表是对Python数据对象的零个或多个引用的有序集合。列表的写法是用方括号括起来、以逗号分隔。空列表简单的用[]表示。列表是异构的,这意味着数据对象不需要全部是同一类型,并且可以集合在一起,赋值给一个变量,如下所示。下面的代码展示了列表中的各种Python数据对象。
>>> [1,3,True,6.5]
[1, 3, True, 6.5]
>>> myList = [1,3,True,6.5]
>>> myList
[1, 3, True, 6.5]
请注意,当Python对列表求值时,会返回列表本身。然而,为了记住后面的列表操作,它的引用需要赋值给一个变量。
切片
由于列表被认为是按顺序排列,所以它们支持许多可以应用于任何Python序列的操作。

注意,列表(序列)的索引从0开始计数。切片操作,myList[1:3],返回一个包含索引从1到3的项的列表、但不包含索引为3的项,即左闭右开。
重复
有时需要初始化一个列表,这可以通过使用重复操作快速完成。例如,
>>> myList = [0] * 6
>>> myList
[0, 0, 0, 0, 0, 0]
除了重复操作符之外,还有一个非常重要的问题是其结果是对序列中的数据对象的引用的重复。通过思考以下代码得到最好的印证:
>>> myList = [1,2,3,4]
>>> A = [myList]*3
>>> print(A)
[[1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4]]
>>> myList[2]=45
>>> print(A)
[[1, 2, 45, 4], [1, 2, 45, 4], [1, 2, 45, 4]]
变量 A 持有三个名为 myList 的原始列表的引用。注意,对 myList 的一个元素的更改,在 A 的所有三种情况中都体现了出来
列表基本操作
>>> myList = [1024, 3, True, 6.5]
>>> myList.append(False)
>>> print(myList)
[1024, 3, True, 6.5, False]
>>> myList.insert(2,4.5)
>>> print(myList)
[1024, 3, 4.5, True, 6.5, False]
>>> print(myList.pop())
False
>>> print(myList)
[1024, 3, 4.5, True, 6.5]
>>> print(myList.pop(1))
3
>>> print(myList)
[1024, 4.5, True, 6.5]
>>> myList.pop(2)
>>> print(myList)
[1024, 4.5, 6.5]
可以看到一些方法,比如 pop,返回一个值,并修改列表。
>>> myList.sort()
>>> print(myList)
[4.5, 6.5, 1024]
>>> myList.reverse()
>>> print(myList)
[1024, 6.5, 4.5]
>>> print(myList.count(6.5))
1
>>> print(myList.index(4.5))
2
>>> myList.remove(6.5)
>>> print(myList)
[1024, 4.5]
>>> del myList[0]
>>> print(myList)
[4.5]
其他的,比如 reverse 和 append,只是简单地修改列表,没有返回值。除此之外,还应该注意到熟悉的 dot 符号,使对象调用方法。
加法
>>> (54).__add__(21)
75
>>> 54+21
75
在此段中,整型对象54来执行它的 add 方法(在Python中称为 __add__),并将它与传过去的21相加,结果是75。当然,通常还是直接把它写成54+21。
range函数
通常与列表一起讨论的一个常见的Python函数是 range 函数。range 产生一个范围对象,表示一系列的值。通过使用 list 函数,可以将 range 对象的值看作一个列表。例子如下:
>>> range(10)
range(0, 10)
>>> list(range(10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> range(5,10)
range(5, 10)
>>> list(range(5,10))
[5, 6, 7, 8, 9]
>>> list(range(5,10,2))
[5, 7, 9]
>>> list(range(10,1,-1))
[10, 9, 8, 7, 6, 5, 4, 3, 2]
range 对象代表一个整数序列。默认情况下,它将从0开始。常用的参数有三个,在特定的点开始和结束,甚至可以跳过某项。
- 在第一个例子中,(10),序列从0开始,递增到10但不包括10。
- 在第二个例子中,范围(5,10)从5开始,递增到10但不包括10。
- 在第三个例子中,范围(5,10,2)类似的执行,但是跳过2(同样,10不包括在内)。
2.2、字符串
字符串是由零个或多个字母、数字和其他符号组成的序列集合。通过使用引号(单引号或双引号)将文字字符串值与标识符区分开来。
>>> "David"
'David'
>>> myName = "David"
>>> myName[3]
'i'
>>> myName*2
'DavidDavid'
>>> len(myName)
5
由于字符串也是序列,所以可以使用上面描述的任何操作。另外,字符串有许多方法,其中一些方法如下所示。

举几个例子:
>>> myName
'David'
>>> myName.upper()
'DAVID'
>>> myName.center(10)
' David '
>>> myName.find('v')
2
>>> myName.split('v')
['Da', 'id']
>>> myName.split()
['David']
其中,split 对于处理数据非常有用。split 将使用一个字符串,并使用分割字符作为分隔点返回字符串列表。在这个例子中,v 是分隔点。如果没有指定分隔点,split 方法会寻找空格字符,如制表符、换行符和空格。
列表和字符串之间的主要区别是,列表可以被修改,而字符串不能,这被称为可变性。列表是可变的;字符串是不可变的。
>>> myList
[1, 3, True, 6.5]
>>> myList[0]=2**10
>>> myList
[1024, 3, True, 6.5]
>>> myName
'David'
>>> myName[0]='X'
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-7-c44c71c6d2f3> in <module>
1 myName = "David"
----> 2 myName[0]='X'
TypeError: 'str' object does not support item assignment
2.3、元组
元组与列表非常相似,因为它们是异构的数据序列。不同之处在于,元组是不可变的,就像字符串一样。任何元组都不能被改变。
作为序列,它们可以使用上面描述的任何操作。例如,
>>> myTuple = (2,True,4.96)
>>> myTuple
(2, True, 4.96)
>>> len(myTuple)
3
>>> myTuple[0]
2
>>> myTuple * 3
(2, True, 4.96, 2, True, 4.96, 2, True, 4.96)
>>> myTuple[0:2]
(2, True)
但是,如果试图改变元组中的一个项,将会得到一个错误。注意,错误消息提供了问题的位置和原因。
>>> myTuple[0] = 1
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-6-a2c5dba3de3b> in <module>
1 myTuple = (2,True,4.96)
----> 2 myTuple[0] = 1
TypeError: 'tuple' object does not support item assignment
2.4、集合
set 是一个无序的, 为空或是更多不可变的Python数据对象集合。集合中的值不允许重复,写在大括号中。空集合由 set() 表示。如下所示。
>>> {3,6,"cat",4.5,False}
{False, 4.5, 3, 6, 'cat'}
>>> mySet = {3,6,"cat",4.5,False}
>>> mySet
{False, 4.5, 3, 6, 'cat'}
>>>
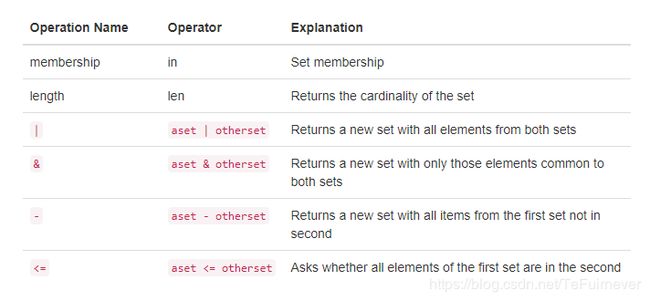
尽管集合不被认为是连续的,但是它们确实支持前面提到的一些熟悉的操作。下表回顾了这些操作,并给出了使用示例。
>>> mySet
{False, 4.5, 3, 6, 'cat'}
>>> len(mySet)
5
>>> False in mySet
True
>>> "dog" in mySet
False
集合支持许多方法,这些方法对于在数学集合中使用它们的人来说应该是熟悉的。 下表提供了总结,它们的使用示例如下。 请注意,联合,交集,子集和差分都有可以使用的运算符。

>>> mySet
{False, 4.5, 3, 6, 'cat'}
>>> yourSet = {99,3,100}
>>> mySet.union(yourSet)
{False, 4.5, 3, 100, 6, 'cat', 99}
>>> mySet | yourSet
{False, 4.5, 3, 100, 6, 'cat', 99}
>>> mySet.intersection(yourSet)
{3}
>>> mySet & yourSet
{3}
>>> mySet.difference(yourSet)
{False, 4.5, 6, 'cat'}
>>> mySet - yourSet
{False, 4.5, 6, 'cat'}
>>> {3,100}.issubset(yourSet)
True
>>> {3,100}<=yourSet
True
>>> mySet.add("house")
>>> mySet
{False, 4.5, 3, 6, 'house', 'cat'}
>>> mySet.remove(4.5)
>>> mySet
{False, 3, 6, 'house', 'cat'}
>>> mySet.pop()
False
>>> mySet
{3, 6, 'house', 'cat'}
>>> mySet.clear()
>>> mySet
set()
2.5、字典
最后一个,Python集合是一个无序的结构,称为字典。字典是一组关联项,其中每一项由一个键和一个值组成。这个 键-值 对通常被写成 key:value。字典的键值对以逗号分隔并用花括号括起来。例如:
>>> capitals = {'Iowa':'DesMoines','Wisconsin':'Madison'}
>>> capitals
{'Wisconsin': 'Madison', 'Iowa': 'DesMoines'}
可以通过它的键来访问它的值,或者通过添加另一个 键-值 对 来操作字典。取值语法除了使用键值而不是使用项目的索引,看起来很像序列取值,添加新值类似。
>>> capitals = {'Iowa':'DesMoines','Wisconsin':'Madison'}
>>> print(capitals['Iowa'])
DesMoines
>>> capitals['Utah']='SaltLakeCity'
>>> print(capitals)
{'Iowa': 'DesMoines', 'Wisconsin': 'Madison', 'Utah': 'SaltLakeCity'}
>>> capitals['California']='Sacramento'
>>> print(capitals)
{'Iowa': 'DesMoines', 'Wisconsin': 'Madison', 'Utah': 'SaltLakeCity', 'California': 'Sacramento'}
>>> print(len(capitals))
4
>>> for k in capitals:
print(capitals[k]," is the capital of ", k)
DesMoines is the capital of Iowa
Madison is the capital of Wisconsin
SaltLakeCity is the capital of Utah
Sacramento is the capital of California
>>> phoneext={'david':1410,'brad':1137}
>>> phoneext
{'brad': 1137, 'david': 1410}
>>> phoneext.keys()
dict_keys(['brad', 'david'])
>>> list(phoneext.keys())
['brad', 'david']
>>> phoneext.values()
dict_values([1137, 1410])
>>> list(phoneext.values())
[1137, 1410]
>>> phoneext.items()
dict_items([('brad', 1137), ('david', 1410)])
>>> list(phoneext.items())
[('brad', 1137), ('david', 1410)]
keys、values 和 items 方法都返回包含感兴趣的值的对象。而 get 方法有两种变体,如果字典里没有对应键,get 将返回空。然而,第二个可选参数可以指定一个返回值。

>>> phoneext={'david':1410,'brad':1137}
>>> phoneext
{'brad': 1137, 'david': 1410}
>>> phoneext.get("kent")
# 返回空说明没有对应的键
>>> phoneext.get("kent","NO ENTRY")
'NO ENTRY'
三、输入和输出
我们经常需要与用户交互,要么获取数据,要么提供某种结果。现今的大多数程序都使用一个对话框来让用户提供某种类型的输入,比如百度的搜索框。

虽然Python确实有创建对话框的方法,但是可以使用一个简单得多的函数 input。它接受单个参数,即字符串。这个字符串通常被称为提示符,因为它包含一些有用的文本,提示用户输入一些东西。
再比如,可以按如下方式调用输入:
>>> aName = input('Please enter your name: ')


无论用户在提示符后面输入什么,都将存储在 aName 变量中。通过使用 input 函数,可以轻松地编写指令,提示用户输入数据,然后将这些数据合并到进一步的处理中。
例如,在接下来的两个语句中,首先询问用户的名称,第二个语句打印基于所提供的字符串的一些简单处理的结果(名字全大写并返回长度)。
>>> aName = input("Please enter your name ")
print("Your name in all capitals is",aName.upper(),
"and has length", len(aName))
需要注意的是,输入函数返回的值将是一个字符串,表示在提示后输入的确切字符。如果想将此字符串解释为另一种类型,必须提供显示的类型转换。
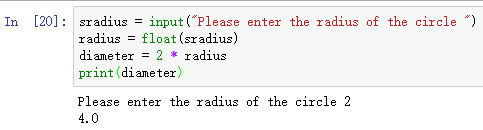
在下面的语句中,由用户输入的字符串被转换为浮点数,以便它可以用于进一步的算术处理。
>>> sradius = input("Please enter the radius of the circle ")
radius = float(sradius)
diameter = 2 * radius
print(diameter)
格式化字符串
打印功能 print 采用零个或更多的参数,并使用单个空格作为默认分隔符来显示它们。可以通过设置 sep 参数来更改分隔符。此外,每次打印在默认情况下都以换行符结尾,可以通过设置结束参数来改变这种行为。这些变化将显示在以下会话中:
>>> print("Hello")
Hello
>>> print("Hello","World")
Hello World
>>> print("Hello","World", sep="***")
Hello***World
>>> print("Hello","World", end="***")
Hello World***
Python提供了一种称为格式化字符串的替代方案。格式化的字符串是一个模板,在这个模板中,结合了保持不变的单词或空格与插入到字符串中的变量的占位符。例如:
>>> print(aName, "is", age, "years old.")
包含词语 is 和 years old,但是名称和年龄将根据执行时的变量值而变化。使用格式化的字符串,改写为
print("%s is %d years old." % (aName, age))
这个简单的例子说明了一个新的字符串表达式。%号是一个字符串操作符,称作 格式化操作符。表达式的左边含有模板或格式字符串,右边包含将被替换成格式字符串的值的集合。
注意,右侧集合中的值的数量与格式字符串中的%字符数相对应,值从左到右依次从集合中获取并插入到格式字符串中。
一个转换字符告诉格式化操作符将插入到字符串中的那个位置的值类型。在上面的例子中,%s指定一个字符串,而%d指定一个整数。其他可能的类型规范包括i、u、f、e、g、c或%。下表总结了各种类型的规范:

除了格式字符之外,还可以在%和格式字符之间包含一个格式修饰符。格式修饰符可以用来对指定字段宽度的值进行左对齐或右对齐。修饰符也可以用来指定字段宽度,以及小数点后的数字。下表解释了这些格式修饰符:

格式操作符的右边是一组值,这些值将被插入到格式字符串中,这个值可能是元组或者字典。
- 如果是一个元组,那么这些值就会按照位置的顺序插入;
- 如果集合是一个字典,那么这些值就会按照键插入键所对应的值。在这种情况下,所有格式字符都必须使用(name)修饰符来指定键的名称。
>>> price = 24
>>> item = "banana"
>>> print("The %s costs %d cents"%(item,price))
The banana costs 24 cents
>>> print("The %+10s costs %5.2f cents"%(item,price))
The banana costs 24.00 cents
>>> print("The %+10s costs %10.2f cents"%(item,price))
The banana costs 24.00 cents
>>> itemdict = {"item":"banana","cost":24}
>>> print("The %(item)s costs %(cost)7.1f cents"%itemdict)
The banana costs 24.0 cents
自从 Python2.6 开始,新增了一种格式化字符串的函数 .format(),它增强了字符串格式化的功能。基本语法是通过 {} 和 : 来代替以前的 %。format 函数可以接受不限个参数,位置可以不按顺序。
>>> print("{} {}".format("hello", "world"))
hello world
>>> print("{0} {1}".format("hello", "world"))
hello world
>>> print("{1} {0} {1}".format("hello", "world"))
world hello world
四、控制结构
算法需要两个重要的控制结构:迭代和选择。
迭代语句
对于迭代,Python提供了一个标准的 while 语句和一个非常强大的 for 语句。只要条件为真,while 语句就会重复一段代码。 例如,
>>> counter = 1
>>> while counter <= 5:
... print("Hello, world")
... counter = counter + 1
Hello, world
Hello, world
Hello, world
Hello, world
Hello, world
在每次重复的开始时评估 while 语句的条件。如果条件为真,则将执行语句主体。由于python语言强制执行的强制缩进模式,很容易看到 while 语句的结构。
while 语句是一个非常通用的迭代结构,在许多情况下,复合条件将控制迭代。
while counter <= 10 and not done:
...
...
另一个迭代结构 for 语句,可以与序列一起使用,用于迭代成员。 例如,
>>> for item in [1,3,6,2,5]:
... print(item)
1
3
6
2
5
将变量 item 指定为列表中[1,3,6,2,5]的每个连续值。 然后执行迭代的主体。 这适用于任何序列(列表,元组和字符串)。
for 语句的一个常见用途是在一系列值上实现明确的迭代。 如下
>>> for item in range(5):
... print(item**2)
...
0
1
4
9
16
>>>
该语句将执行五次 print 功能,range 函数将返回表示序列0,1,2,3,4的范围对象,并且每个值将分配给变量 item,然后计算该值平方并打印。
此迭代结构还可以用于处理字符串的每个字符,以下代码输出的是所有单词中字母的列表:
>>> wordlist = ['cat','dog','rabbit']
letterlist = [ ]
for aword in wordlist:
for aletter in aword:
letterlist.append(aletter)
print(letterlist)
['c', 'a', 't', 'd', 'o', 'g', 'r', 'a', 'b', 'b', 'i', 't']
选择语句
选择语句允许程序员提出问题,然后根据结果执行不同的操作。 大多数编程语言都提供了两个版本:ifelse 和 if。举一个分数判定的例子:
if score >= 90:
print('A')
else:
if score >=80:
print('B')
else:
if score >= 70:
print('C')
else:
if score >= 60:
print('D')
else:
print('F')
此片段将为 score 的值进行判定。 如果分数大于或等于90,则语句将打印A;如果不是(else),则询问下一个问题。 如果分数大于或等于80,那么它必须在80到89之间,因为第一个问题的答案是错误的。 在这种情况下,打印B。 您可以看到Python缩进模式有助于理解 if 和 else 之间的关联而无需任何其他语法元素。
此类嵌套选择的替代语法是使用 elif 关键字。将 else 和下一个 if 组合起来,以消除对额外嵌套级别的需要。 如果所有其他条件都失败,则仍需要最终的 else 来提供默认情况。代码如下:
if score >= 90:
print('A')
elif score >=80:
print('B')
elif score >= 70:
print('C')
elif score >= 60:
print('D')
else:
print('F')
有一种使用使用迭代和选择构造的替代方法来创建一个列表,称为 list comprehension。例如,如果想要创建前10个完美正方形的列表,可以使用for语句:
>>> sqlist=[]
>>> for x in range(1,11):
sqlist.append(x*x)
>>> sqlist
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
也可以一步完成:
>>> sqlist=[x*x for x in range(1,11)]
>>> sqlist
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
列表推导的一般语法还允许添加选择标准,以便仅添加某些项。 例如,
>>> sqlist=[x*x for x in range(1,11) if x%2 != 0]
>>> sqlist
[1, 9, 25, 49, 81]
此列表推导构造了一个列表,该列表仅包含1到10范围内的奇数的平方。任何支持迭代的序列都可以在列表推导中用于构造新列表。
>>>[ch.upper() for ch in 'comprehension' if ch not in 'aeiou']
['C', 'M', 'P', 'R', 'H', 'N', 'S', 'N']
五、处理异常
在编写程序时通常会出现两种类型的错误。
- 第一个类型的错误称为 语法错误,仅仅意味着程序员在语句或表达式的结构中犯了一个错误。
例如,写一个 for 语句而忘记冒号是错误的。
>>> for i in range(10)
File "" , line 1
for i in range(10)
^
SyntaxError: invalid syntax
在这种情况下,Python解释器发现它不能完成这个指令的处理,因为不符合语言的规则。当第一次学习一门语言时,语法错误通常会更频繁。
- 另一种类型的错误称为 逻辑错误,表示程序执行但给出错误结果的情况。 这可能是由于基础算法中的错误或该算法的转换错误。
在某些情况下,逻辑错误会导致非常糟糕的情况。例如,思考下面的会话,让用户输入一个整数,然后从数学库调用平方根函数。如果用户输入大于或等于0的值,打印将显示平方根。但是,如果用户输入负值,平方根函数将报出 ValueError 异常。
>>> anumber = int(input("Please enter an integer "))# 输入 -23
Please enter an integer -23
>>> import math
>>> print(math.sqrt(anumber))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-11-3c97b1b97120> in <module>
1 import math
----> 2 print(math.sqrt(anumber))
ValueError: math domain error
当一个异常发生时,我们说它已经被“抛出”了。使用 try 语句处理所提出的异常。在 try 块中调用 print 函数来处理这个异常。相应的 except 块“捕获”异常,并在发生异常时将消息打印给用户。例如:
>>> try:
print(math.sqrt(anumber))
except:
print("Bad Value for square root")
print("Using absolute value instead")
print(math.sqrt(abs(anumber)))
Bad Value for square root
Using absolute value instead
4.79583152331
它将捕获 sqrt 引发的异常,将消息打印回用户并使用绝对值来确保采用非负数的平方根。 这意味着程序不会终止,而是继续执行下一个语句。
程序员也可以通过使用 raise 语句来引发运行时异常。 例如,可以先检查该值,然后引发自己的异常,而不是使用负数调用平方根函数。 下面的代码片段显示了创建新的 RuntimeError 异常的结果。 请注意,程序仍然会终止,但现在导致终止的异常是程序员明确创建的。
>>> if anumber < 0:
... raise RuntimeError("You can't use a negative number")
... else:
... print(math.sqrt(anumber))
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-18-424977cff197> in <module>
1 if anumber < 0:
----> 2 raise RuntimeError("You can't use a negative number")
3 else:
4 print(math.sqrt(anumber))
RuntimeError: You can't use a negative number
除了上面显示的 RuntimeError 之外,还可以引发多种异常。
| 异常名称 | 描述 |
|---|---|
| BaseException | 所有异常的基类 |
| SystemExit | 解释器请求退出 |
| KeyboardInterrupt | 用户中断执行(通常是输入^C) |
| Exception | 常规错误的基类 |
| StopIteration | 迭代器没有更多的值 |
| GeneratorExit | 生成器(generator)发生异常来通知退出 |
| StandardError | 所有的内建标准异常的基类 |
| ArithmeticError | 所有数值计算错误的基类 |
| FloatingPointError | 浮点计算错误 |
| OverflowError | 数值运算超出最大限制 |
| ZeroDivisionError | 除(或取模)零 (所有数据类型) |
| AssertionError | 断言语句失败 |
| AttributeError | 对象没有这个属性 |
| EOFError | 没有内建输入,到达EOF 标记 |
| EnvironmentError | 操作系统错误的基类 |
| IOError | 输入/输出操作失败 |
| OSError | 操作系统错误 |
| WindowsError | 系统调用失败 |
| ImportError | 导入模块/对象失败 |
| LookupError | 无效数据查询的基类 |
| IndexError | 序列中没有此索引(index) |
| KeyError | 映射中没有这个键 |
| MemoryError | 内存溢出错误(对于Python 解释器不是致命的) |
| NameError | 未声明/初始化对象 (没有属性) |
| UnboundLocalError | 访问未初始化的本地变量 |
| ReferenceError | 弱引用(Weak reference)试图访问已经垃圾回收了的对象 |
| RuntimeError | 一般的运行时错误 |
| NotImplementedError | 尚未实现的方法 |
| SyntaxError | Python 语法错误 |
| IndentationError | 缩进错误 |
| TabError | Tab 和空格混用 |
| SystemError | 一般的解释器系统错误 |
| TypeError | 对类型无效的操作 |
| ValueError | 传入无效的参数 |
| UnicodeError | Unicode 相关的错误 |
| UnicodeDecodeError | Unicode 解码时的错误 |
| UnicodeEncodeError | Unicode 编码时错误 |
| UnicodeTranslateError | Unicode 转换时错误 |
| Warning | 警告的基类 |
| DeprecationWarning | 关于被弃用的特征的警告 |
| FutureWarning | 关于构造将来语义会有改变的警告 |
| OverflowWarning | 旧的关于自动提升为长整型(long)的警告 |
| PendingDeprecationWarning | 关于特性将会被废弃的警告 |
| RuntimeWarning | 可疑的运行时行为(runtime behavior)的警告 |
| SyntaxWarning | 可疑的语法的警告 |
| UserWarning | 用户代码生成的警告 |
六、定义函数
一般来说,可以通过定义一个函数来隐藏任何计算的细节。一个函数定义需要一个 名称、一组 参数 和一个 函数体。例如,下面定义的简单函数返回传入的值的平方。
>>> def square(n):
... return n**2
>>> square(3)
9
>>> square(square(3))
81
这个函数定义的语法包括 名称、square 和一个圆括号括起来的 正式参数列表。对于这个函数,n 是唯一的正式参数,这表明 square 只需要一段数据就可以完成它的工作。这些细节隐藏在 盒子里,简单地计算出 n**2 的结果并返回它。为调用 square 函数,可以传入一个实际的参数值来让Python计算他。
注意,对 square 的调用会返回一个整数,该整数又可以被传递给另一个调用。
除此之外,还可以使用一种叫做 牛顿法 的著名技术来实现平方根函数。牛顿法用近似平方根来的执行迭代运算,该计算收敛于正确的值。等式 newguess = 1/2 *(oldguess + n/oldguess) 取 n 值,并通过在随后的迭代中使每个 newguess 成为 oldguess 来反复猜测平方根,最初始的猜测是 n/2。
例子如下:
def squareroot(n):
root = n/2 #initial guess will be 1/2 of n
for k in range(20):
root = (1/2)*(root + (n / root))
return root
封装好一个函数,然后调用这个函数就可以实现这个功能。
>>>squareroot(9)
3.0
>>>squareroot(4563)
67.549981495186216
七、面向对象编程:定义类
Python是一种 面向对象 的编程语言,面向对象编程语言中最强大的功能之一是允许程序员(问题解决者)创建新类,以模拟解决问题所需的数据。
请记住,抽象数据类型被用来提供数据对象的外观(其状态)及其可以执行的操作(其方法)的逻辑描述。 通过构建实现抽象数据类型的类,程序员可以利用抽象过程,同时提供在程序中实际使用抽象所需的详细信息,什么是抽象?
定义:从具体事物抽出、概括出它们共同的方面、本质属性与关系等,而将个别的、非本质的方面、属性与关系舍弃,这种思维过程,称为 抽象。
每当我们想要实现抽象数据类型时,都会使用新类。
7.1、一个分数类
一个非常常见的例子,展示实现用户定义的类的细节,就是构造一个类来实现抽象的分数数据类型。到现在为止,已经看到Python提供了许多供我们使用的数字类,也就是 math 第三方库。
然而,有时候,能够创建 看起来像 分数的数据对象是最合适的。像3/5这样的分数由两部分组成,最上面的值,也就是分子,可以是任意整数。底部的值,叫做分母,可以是大于0的整数(负分数有负的分子)。
创建的类名字是 Fraction,Fraction 类型的操作将允许 Fraction 数据对象的行为与任何其他数值一样,需要能够对分数进行加,减,乘和除,还希望能够使用标准的 斜杠 形式显示分数,例如3/5。 此外,所有分数方法都应以最低项返回结果,这样无论执行何种计算,总是以最常见的形式结束。
在Python中,通过提供一个名称和一组在语法上类似于函数定义的方法定义来定义一个新类。 对于这个例子,定义方法的框架如下:
class Fraction:
#the methods go here
所有类应提供的第一个方法是构造函数,构造函数定义了数据对象的创建方式。 要创建 Fraction 对象,需要提供两个数据,分子和分母。 在Python中,构造函数方法始终称为 __init __(init 之前和之后的两个下划线),如下所示:
class Fraction:
def __init__(self,top,bottom):
self.num = top
self.den = bottom
注意,形式参数列表包含三个项目(self,top,bottom)。 self 是一个特殊参数,将始终用作返回对象本身的引用。 它必须始终是第一个形式参数; 但是,在调用时永远不会给出实际的参数值。构造函数中的符号 self.num 定义了 Fraction 对象,使其具有名为 num 的内部数据对象作为其状态的一部分。同样,self.den 创建了分母。两个正式参数做初始化赋值,允许新的分数对象知道它的起始值。
要创建分数类的实例,必须调用构造函数。这发生在使用类名并传递必要状态的实际值(注意,从不直接调用 __init__)。 例如,
myfraction = Fraction(3,5)
创建一个名为 myfraction 的对象,表示分数3/5(五分之三)。下图显示了此对象,因为它当前已实现。
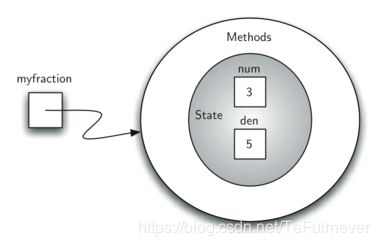
下一步是实现抽象数据类型所需的行为。 首先,考虑一下当我们尝试打印 Fraction 对象时会发生什么。
>>> myf = Fraction(3,5)
>>> print(myf)
<__main__.Fraction instance at 0x409b1acc>
fraction 对象 myf 不知道如何响应此打印请求。 print 函数要求对象将自身转换为字符串,以便可以将字符串写入输出。 myf 唯一的选择是显示存储在变量中的实际引用(地址本身),然而很明显这不是我们想要的。
有两种方法。 一种是定义一个名为 show 的方法,它允许 Fraction 对象将自己打印为字符串。 代码如下:
def show(self):
print(self.num,"/",self.den)
>>> myf = Fraction(3,5)
>>> myf.show()
3 / 5
>>> print(myf)
<__main__.Fraction instance at 0x40bce9ac>
如果像以前一样创建Fraction对象,可以要求它显示自己,换句话说,以适当的格式打印自己。 不幸的是,这一般不起作用。 为了使打印正常工作,我们需要告诉 Fraction 类如何将自身转换为字符串,这是打印功能为了完成其工作所需要的。
在Python中,所有类都提供了一组标准方法,但可能无法正常工作。 其中之一 __str__ 是一种将对象转换为字符串的方法。 正如已经看到的,此方法的默认实现是返回实例地址字符串。我们需要做的是为这种方法提供 更好 的实现。为此,只需定义一个名为 __str__ 的方法,并为其提供一个新的实现,如下所示。
def __str__(self):
return str(self.num)+"/"+str(self.den)
>>> myf = Fraction(3,5)
>>> print(myf)
3/5
>>> print("I ate", myf, "of the pizza")
I ate 3/5 of the pizza
>>> myf.__str__()
'3/5'
>>> str(myf)
'3/5'
除了特殊参数 self 之外,该定义不需要任何其他信息。 反过来,该方法将通过让每个内部状态数据转换为字符串,然后使用字符串连接在字符串之间放置/字符来构建字符串表示。 每当要求 Fraction 对象将其自身转换为字符串时,将返回结果字符串。
我们可以为新的 Fraction 类覆盖许多其他方法,其中一些最重要的是基本的算术运算。 我们希望能够创建两个 Fraction 对象,然后使用标准的 + 符号将它们添加到一起。如下:
>>> f1 = Fraction(1,4)
>>> f2 = Fraction(1,2)
>>> f1+f2
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-20-0210d543cddb> in <module>
1 f1 = Fraction(1,4)
2 f2 = Fraction(1,2)
----> 3 f1+f2
TypeError: unsupported operand type(s) for +: 'Fraction' and 'Fraction'
出现错误的问题是因为 + 运算符不理解 Fraction 操作数。如何解决这个问题?可以通过为 Fraction 类提供一个覆盖 add 方法的方法来解决这个问题。 在Python中,此方法称为 __add__,这个我们在前面加法中提到过它,需要两个参数,第一个是 self,总是需要,第二个代表表达式中的另一个操作数。 例如,
f1.__add__(f2)
这个操作会要求 Fraction 对象 f1 将 Fraction 对象 f2 添加到自身,这可以用标准符号 f1 + f2 编写。但是两个分数必须具有相同的分母才能添加。 确保它们具有相同分母的最简单方法是简单地使用两个分母的乘积作为公分母,以便 a/b + c/d = ad/bd + cb/bd = (ad + cb)/bd 实现。如下所示:
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
return Fraction(newnum,newden)
>>> f1=Fraction(1,4)
>>> f2=Fraction(1,2)
>>> f3=f1+f2
>>> print(f3)
6/8
附加函数返回一个新的 Fraction 对象,分别是经过变换后的分子和分母。可以用这个方法来写一个包含分数的标准算术表达式,赋值加法的结果,然后打印我们的结果。得到 6/8 是正确的结果 (1/4 + 1/2),但它不是 最低术语 表示,最好的代表是 3/4。 为了确保结果总是在最低的条件下,需要一个知道如何减少分数的辅助函数。 此函数需要查找最大公约数或GCD,然后可以将分子和分母除以GCD,结果将减少到最低项。用于求出最大公约数的最着名算法是 欧几里德算法,将在后面做详细地讨论,这里直接给出代码。
def gcd(m,n):
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
print(gcd(20,10))
现在我们可以使用此函数来帮助减少任何分数。 为了将分数置于最低项中,我们将分子和分母除以它们的最大公约数。 因此,对于分数6/8,最大公约数为2.将顶部和底部除以2会创建一个新的分数3/4,代码如下:
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
>>> f1=Fraction(1,4)
>>> f2=Fraction(1,2)
>>> f3=f1+f2
>>> print(f3)
3/4
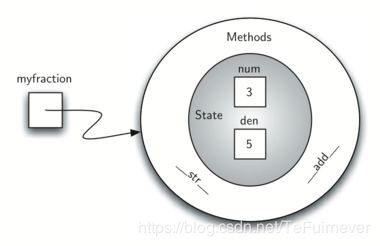
我们的分数对象现在有两个非常有用的方法,如上图所示,分别是 __add 和 __str,下一步需要在示例 Fraction 类中包含的另一组方法将两个分数相互比较。假设有两个 Fraction 对象,f1 和 f2,f1 == f2 只有在引用同一个对象时才为 True。具有相同分子和分母的两个不同对象在此实现下将不相等,这称为浅等式,如下图:
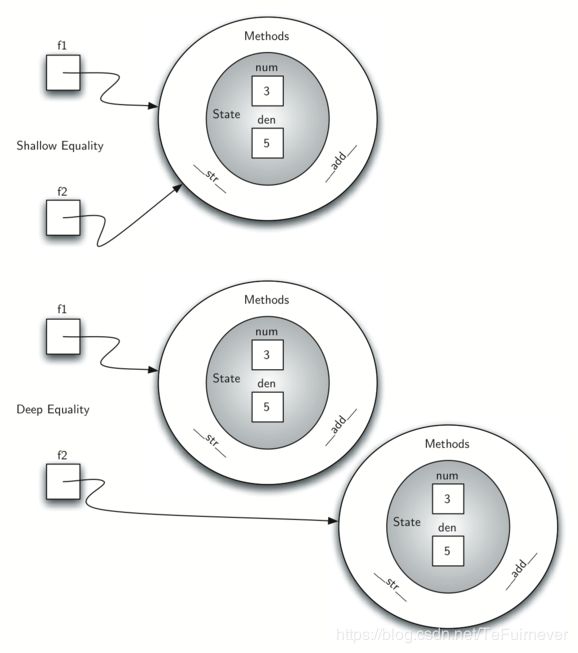
通过覆盖 __eq__ 方法,通过相同的值创建深等式,如上图,而不是相同的引用。__eq__ 方法是任何类中都可用的另一种标准方法。__eq__ 方法比较两个对象,如果它们的值相同则返回True,否则返回False。
在 Fraction 类中,可以通过再次将两个分数放在通用项中然后比较分子来实现 __eq__ 方法,代码如下:
def __eq__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum == secondnum
到目前为止,完整的 Fraction 类如下所示:
def gcd(m,n):
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
class Fraction:
def __init__(self,top,bottom):
self.num = top
self.den = bottom
def __str__(self):
return str(self.num)+"/"+str(self.den)
def show(self):
print(self.num,"/",self.den)
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + \
self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
def __eq__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum == secondnum
x = Fraction(1,2)
y = Fraction(2,3)
print(x+y)
print(x == y)
7.2、逻辑门和电路
最后这一部分将介绍面向对象编程的另一个重要方面——继承。继承是一个类与另一个类相关联的能力,与人们彼此相关的方式非常相似,即儿女继承父母的特征。 类似地,Python子类可以从父类继承特征数据和行为,这些类通常称为子类和超类。

上图显示了内置的Python集合及其相互之间的关系,这种关系结构可以称为 继承结构。 例如,列表是有序集合的子类。 在这种情况下,列表称为子级,将序列称为父级(或子类列表和超类序列)。 这通常被称为 IS-A Relationship(列表IS-A游戏集合)。 这意味着列表从序列继承了重要的特征,即底层数据的排序和连接,重复和索引等操作。列表,元组和字符串都是有序集合类型。 它们都继承了常见的数据组织方式和操作。 但是,根据数据是否是同构的以及集合是否不可变,它们中的每一个都是不同的。 孩子们都从父母那里获益,并通过增加额外的特征来区分自己。
通过以这种继承方式来组织类,面向对象的编程语言允许扩展先前编写的代码以满足新情况的需要。 此外,通过以这种继承方式来组织数据,可以更好地理解存在的关系,更有效地构建抽象表示。
为了进一步探索这个特性,我们将构造仿真,仿真一个模拟数字电路的应用程序,该模拟的基本构建块是逻辑门。 这些电子开关代表其输入和输出之间的布尔代数关系。
- 与门有两条输入线,每条输入线可以是0或1(分别代表False或True)。 如果两个输入行的值都为1,则结果输出为1。但是,如果输入行中的任何一个或两个为0,则结果为0。
- 或门也有两个输入行,如果一个或两个输入行为1,则输出值为1。
- 非门与其他两个门的不同之处在于它们只有一条输入线,输出值与输入值完全相反。 如果输入出现0,则在输出上产生1;类似地,1产生0。
下图显示了这些门中的每一个在数电中通常如何表示的。每个门还有一个真值表,显示由门执行的输入到输出映射。如果你学过数电,这应该是是很简单的;如果没学过也没事,就是上面提到的每一个门的特点。
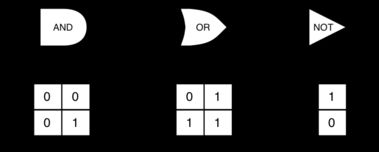
通过以各种模式组合这些门,然后应用一组输入值,可以构建一个具有逻辑功能的电路。下图显示了一个由两个与门,一个或门和一个非门组成的电路。
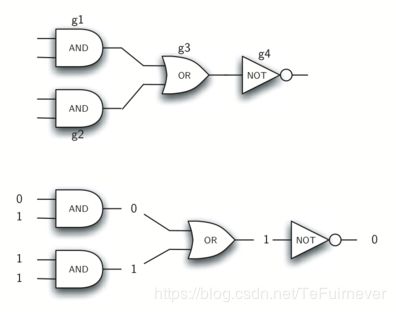
来自两个与门的输出线直接馈入或门,或门产生的输出提供给非门。 如果将一组输入值应用于四个输入行(每个与门两个),则处理这些值并在非门的输出处显示结果。上图还给出了一个带有值的示例,可以感受一下,0与1为0,1与1为1,0或1为1,1非为0,很简单吧 。
为了实现电路,我们将首先构建逻辑门的表示。 逻辑门很容易组织成一个类继承层次结构,如下图。

在继承结构的顶部,LogicGate 类代表逻辑门的最一般特征:即门的标签和输出线。 下一级子类将逻辑门分为两个系列,即具有一个输入线的系列和具有两个输入线的系列。 在此之下,每个的特定逻辑功能出现。
先从最常见的 LogicGate 开始实现这些类。 如前所述,每扇门都有一个识别标签和一条输出线。 此外,还需要一种方法,允许门的用户从门上请求标签。
每个逻辑门需要的另一个行为是知道其输出值的能力,这将要求门基于当前输入执行适当的逻辑。 为了产生输出,门需要知道该逻辑具体是什么。 这意味着调用一个方法来执行逻辑计算。 完整的类如下所示:
class LogicGate:
def __init__(self,n):
self.label = n
self.output = None
def getLabel(self):
return self.label
def getOutput(self):
self.output = self.performGateLogic()
return self.output
根据输入线的数量对逻辑门进行了分类。 与门有两条输入线。 或门也有两条输入线。 非门有一条输入线。 BinaryGate 类将是 LogicGate 的子类,并将添加两个输入行。 UnaryGate 类也将是 LogicGate 的子类,但只有一个输入行。 在计算机电路设计中,这些线有时被称为“引脚”,因此我们将在实现中使用该术语。
class BinaryGate(LogicGate):
def __init__(self,n):
LogicGate.__init__(self,n)
self.pinA = None
self.pinB = None
def getPinA(self):
return int(input("Enter Pin A input for gate "+ self.getLabel()+"-->"))
def getPinB(self):
return int(input("Enter Pin B input for gate "+ self.getLabel()+"-->"))
class UnaryGate(LogicGate):
def __init__(self,n):
LogicGate.__init__(self,n)
self.pin = None
def getPin(self):
return int(input("Enter Pin input for gate "+ self.getLabel()+"-->"))
这两个类中的构造函数都是使用父类的 __init__ 方法显式调用父类的构造函数。 在创建 BinaryGate 类的实例时,首先要初始化从 LogicGate 继承的任何数据项。 在这种情况下,意味着门的标签。 然后构造函数继续添加两条输入线(pinA和pinB)。 这是构建类层次结构时应始终使用的非常常见的模式,子类构造函数需要调用父类构造函数,然后继续使用它们自己的区分数据。
BinaryGate 类添加的唯一行为是从两个输入行获取值的能力。 由于这些值来自某些外部位置,只需通过输入语句询问用户即可。 除了只有一个输入行之外,UnaryGate 类也会进行相同的实现。
现在有了一个针对门的通用类,这取决于输入行的数量,我们可以构建具有独特行为的特定门。例如,AndGate 类将是BinaryGate 的子类,因为与门有两条输入线。 和以前一样,构造函数的第一行调用父类构造函数(BinaryGate),后者又调用其父类构造函数(LogicGate)。 请注意,AndGate 类不提供任何新数据,因为它继承了两个输入行,一个输出行和一个标签。
class AndGate(BinaryGate):
def __init__(self,n):
BinaryGate.__init__(self,n)
def performGateLogic(self):
a = self.getPinA()
b = self.getPinB()
if a==1 and b==1:
return 1
else:
return 0
AndGate 唯一需要添加的是执行前面描述的布尔操作的特定行为。 这是可以提供 performGateLogic 方法的地方。 对于 AND 门,此方法首先必须获取两个输入值,然后仅在两个输入值均为1时返回1。完整类如下所示。
>>> g1 = AndGate("G1")
>>> g1.getOutput()
Enter Pin A input for gate G1-->1
Enter Pin B input for gate G1-->0
0
对于或门和非门,可以进行相同的开发。 OrGate 类也将是 BinaryGate 的子类,NotGate 类将扩展 UnaryGate 类。 这两个类都需要提供自己的 performGateLogic 函数,因为这是它们的特定行为。我们可以使用单个门,首先构造一个门类的实例,然后得到门的输出(这将反过来需要提供输入)。 例如:
>>> g2 = OrGate("G2")
>>> g2.getOutput()
Enter Pin A input for gate G2-->1
Enter Pin B input for gate G2-->1
1
>>> g2.getOutput()
Enter Pin A input for gate G2-->0
Enter Pin B input for gate G2-->0
0
>>> g3 = NotGate("G3")
>>> g3.getOutput()
Enter Pin input for gate G3-->0
1
现在已经完成了基本的工作,可以将注意力转向构建电路。 为了创建一个电路,我们需要将门连接在一起,一个输出另一个输入。 为此,我们将实现一个名为 Connector 的新类。Connector 类不会驻留在门层次结构中。 然而,它将使用门层次结构,因为每个连接器将具有两个门,一个在两端,如下图。
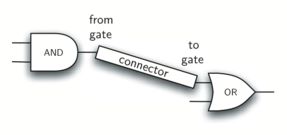
现在,使用 Connector 类,我们说连接器 HAS-A LogicGate 意味着连接器将包含 LogicGate 类的实例但不是层次结构的一部分。 在设计类时,区分具有 IS-A 关系(需要继承)和具有 HAS-A 关系(没有继承)的类非常重要。
Connector类的代码如下。
class Connector:
def __init__(self, fgate, tgate):
self.fromgate = fgate
self.togate = tgate
tgate.setNextPin(self)
def getFrom(self):
return self.fromgate
def getTo(self):
return self.togate
每个连接器对象内的两个门实例将被称为 fromgate 和 togate,识别出数据值将从一个门的输出“流动”到下一个门的输入线。 对 setNextPin 的调用对于建立连接非常重要,代码如下。
def setNextPin(self,source):
if self.pinA == None:
self.pinA = source
else:
if self.pinB == None:
self.pinB = source
else:
raise RuntimeError("Error: NO EMPTY PINS")
需要将此方法添加到我们的门类中,以便每个 togate 可以为连接选择正确的输入行。在 BinaryGate 类中,对于具有两条可能输入线的门,连接器必须仅连接到一条线。 如果它们都可用,我们将默认选择 pinA。 如果 pinA 已经连接,那么我们将选择 pinB,无法连接到没有可用输入线的门。
现在可以从两个位置获取输入:外部,以及连接到该输入线的门的输出。 这需要更改 getPinA 和 getPinB 方法,代码如下。
def getPinA(self):
if self.pinA == None:
return input("Enter Pin A input for gate " + self.getName()+"-->")
else:
return self.pinA.getFrom().getOutput()
如果输入行没有连接到任何内容(空),则像以前一样向外部询问用户。 但是,如果存在连接,则访问连接并检索 fromgate 的输出值,这反过来导致该门处理其逻辑。 这一直持续到所有输入都可用并且最终输出值成为所讨论的门的所需输入。 从某种意义上说,电路向后工作以找到最终产生输出所需的输入。
以下片段构建了本节前面所示的电路:
>>> g1 = AndGate("G1")
>>> g2 = AndGate("G2")
>>> g3 = OrGate("G3")
>>> g4 = NotGate("G4")
>>> c1 = Connector(g1,g3)
>>> c2 = Connector(g2,g3)
>>> c3 = Connector(g3,g4)
两个与门(g1和g2)的输出连接到或门(g3),输出连接到非门(g4),非门的输出是整个电路的输出。 例如:
>>> g4.getOutput()
Pin A input for gate G1-->0
Pin B input for gate G1-->1
Pin A input for gate G2-->1
Pin B input for gate G2-->1
0
完整代码如下,尝试一下:
class LogicGate:
def __init__(self,n):
self.name = n
self.output = None
def getName(self):
return self.name
def getOutput(self):
self.output = self.performGateLogic()
return self.output
class BinaryGate(LogicGate):
def __init__(self,n):
LogicGate.__init__(self,n)
self.pinA = None
self.pinB = None
def getPinA(self):
if self.pinA == None:
return int(input("Enter Pin A input for gate "+self.getName()+"-->"))
else:
return self.pinA.getFrom().getOutput()
def getPinB(self):
if self.pinB == None:
return int(input("Enter Pin B input for gate "+self.getName()+"-->"))
else:
return self.pinB.getFrom().getOutput()
def setNextPin(self,source):
if self.pinA == None:
self.pinA = source
else:
if self.pinB == None:
self.pinB = source
else:
print("Cannot Connect: NO EMPTY PINS on this gate")
class AndGate(BinaryGate):
def __init__(self,n):
BinaryGate.__init__(self,n)
def performGateLogic(self):
a = self.getPinA()
b = self.getPinB()
if a==1 and b==1:
return 1
else:
return 0
class OrGate(BinaryGate):
def __init__(self,n):
BinaryGate.__init__(self,n)
def performGateLogic(self):
a = self.getPinA()
b = self.getPinB()
if a ==1 or b==1:
return 1
else:
return 0
class UnaryGate(LogicGate):
def __init__(self,n):
LogicGate.__init__(self,n)
self.pin = None
def getPin(self):
if self.pin == None:
return int(input("Enter Pin input for gate "+self.getName()+"-->"))
else:
return self.pin.getFrom().getOutput()
def setNextPin(self,source):
if self.pin == None:
self.pin = source
else:
print("Cannot Connect: NO EMPTY PINS on this gate")
class NotGate(UnaryGate):
def __init__(self,n):
UnaryGate.__init__(self,n)
def performGateLogic(self):
if self.getPin():
return 0
else:
return 1
class Connector:
def __init__(self, fgate, tgate):
self.fromgate = fgate
self.togate = tgate
tgate.setNextPin(self)
def getFrom(self):
return self.fromgate
def getTo(self):
return self.togate
def main():
g1 = AndGate("G1")
g2 = AndGate("G2")
g3 = OrGate("G3")
g4 = NotGate("G4")
c1 = Connector(g1,g3)
c2 = Connector(g2,g3)
c3 = Connector(g3,g4)
print(g4.getOutput())
main()
八、总结
- 计算机科学是解决问题的研究。
- 计算机科学使用抽象作为表示过程和数据的工具。
- 抽象的数据类型允许程序员通过隐藏数据的细节来管理问题领域的复杂性。
- Python是一种强大但易于使用的面向对象语言。
- 列表、元组和字符串都是用Python有序集合构建的。
- 字典和集合是无序的数据集合。
- 类允许程序员实现抽象的数据类型。
- 程序员可以重写标准方法,并创建新的方法。
- 类可以被组织成层次结构。
- 类构造器应该总是调用其父节点的构造函数,然后继续使用自己的数据和行为。
参考文章
- 《problem solving with algorithms and data structure using python》
- https://github.com/facert/python-data-structure-cn
- https://www.runoob.com/python/python-tutorial.html