在SSE图像算法优化系列五:超高速指数模糊算法的实现和优化(10000*10000在100ms左右实现) 一文中,我曾经说过优化后的ExpBlur比BoxBlur还要快,那个时候我比较的BoxBlur算法是通过积分图+SSE实现的,我在09年另外一个博客账号上曾经提供过一篇这个文章彩色图像高速模糊之懒惰算法,里面也介绍了一种快速的图像模糊算法,这个算法的执行时间基本也是和半径无关的。在今年的SSE优化学习之路上我曾经也考虑过将该算法使用SSE实现,但当时觉得这个算法逐像素同时逐行都是前后依赖的(单纯的逐像素依赖算法我在指数模糊里有提到如何用SSE优化),是无法用SSE处理的,一直没考虑,直到最近有朋友提出某个基于局部局方差的算法希望能提速,我又再次触发灵感,终于将这种算法也实现的指令集实现,并且测试速度比积分图快二倍,比解析opencv中Box Filter的实现并提出进一步加速的方案(源码共享)这篇文章的速度快3倍,比opencv的cvSmooth函数快5倍,在一台老旧的I3笔记本上处理3000*2000的灰度图达到了6ms的速度,本文分享该优化过程并提供灰度版本的优化代码供大家学习和讨论。
在彩色图像高速模糊之懒惰算法一文附带的代码中(VB6的代码)是针对24位的图像,为了讨论方便,我们先贴出8位灰度的C++的代码:
1 ///2 /// 按照Tile方式进行数据的扩展,得到扩展后在原尺寸中的位置,以0为下标。 3 /// 4 int IM_GetMirrorPos(int Length, int Pos) 5 { 6 if (Pos < 0) 7 return -Pos; 8 else if (Pos >= Length) 9 return Length + Length - Pos - 2; 10 else 11 return Pos; 12 } 13 14 void FillLeftAndRight_Mirror_C(int *Array, int Length, int Radius) 15 { 16 for (int X = 0; X < Radius; X++) 17 { 18 Array[X] = Array[Radius + Radius - X]; 19 Array[Radius + Length + X] = Array[Radius + Length - X - 2]; 20 } 21 } 22 23 int SumofArray_C(int *Array, int Length) 24 { 25 int Sum = 0; 26 for (int X = 0; X < Length; X++) 27 { 28 Sum += Array[X]; 29 } 30 return Sum; 31 } 32 33 /// 34 /// 将整数限幅到字节数据类型。 35 /// 36 inline unsigned char IM_ClampToByte(int Value) // 现代PC还是这样直接写快些 37 { 38 if (Value < 0) 39 return 0; 40 else if (Value > 255) 41 return 255; 42 else 43 return (unsigned char)Value; 44 //return ((Value | ((signed int)(255 - Value) >> 31)) & ~((signed int)Value >> 31)); 45 } 46 47 int IM_BoxBlur_C(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride, int Radius) 48 { 49 int Channel = Stride / Width; 50 if ((Src == NULL) || (Dest == NULL)) return IM_STATUS_NULLREFRENCE; 51 if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; 52 if (Radius < 1) return IM_STATUS_INVALIDPARAMETER; 53 if ((Channel != 1) && (Channel != 3) && (Channel != 4)) return IM_STATUS_NOTSUPPORTED; 54 55 Radius = IM_Min(IM_Min(Radius, Width - 1), Height - 1); // 由于镜像的需求,要求半径不能大于宽度或高度-1的数据 56 57 int SampleAmount = (2 * Radius + 1) * (2 * Radius + 1); 58 float Inv = 1.0 / SampleAmount; 59 60 int *ColValue = (int *)malloc((Width + Radius + Radius) * (Channel == 1 ? Channel : 4) * sizeof(int)); 61 int *ColOffset = (int *)malloc((Height + Radius + Radius) * sizeof(int)); 62 if ((ColValue == NULL) || (ColOffset == NULL)) 63 { 64 if (ColValue != NULL) free(ColValue); 65 if (ColOffset != NULL) free(ColOffset); 66 return IM_STATUS_OUTOFMEMORY; 67 } 68 for (int Y = 0; Y < Height + Radius + Radius; Y++) 69 ColOffset[Y] = IM_GetMirrorPos(Height, Y - Radius); 70 71 if (Channel == 1) 72 { 73 for (int Y = 0; Y < Height; Y++) 74 { 75 unsigned char *LinePD = Dest + Y * Stride; 76 if (Y == 0) 77 { 78 memset(ColValue + Radius, 0, Width * sizeof(int)); 79 for (int Z = -Radius; Z <= Radius; Z++) 80 { 81 unsigned char *LinePS = Src + ColOffset[Z + Radius] * Stride; 82 for (int X = 0; X < Width; X++) 83 { 84 ColValue[X + Radius] += LinePS[X]; // 更新列数据 85 } 86 } 87 } 88 else 89 { 90 unsigned char *RowMoveOut = Src + ColOffset[Y - 1] * Stride; // 即将减去的那一行的首地址 91 unsigned char *RowMoveIn = Src + ColOffset[Y + Radius + Radius] * Stride; // 即将加上的那一行的首地址 92 for (int X = 0; X < Width; X++) 93 { 94 ColValue[X + Radius] -= RowMoveOut[X] - RowMoveIn[X]; // 更新列数据 95 } 96 } 97 FillLeftAndRight_Mirror_C(ColValue, Width, Radius); // 镜像填充左右数据 98 int LastSum = SumofArray_C(ColValue, Radius * 2 + 1); // 处理每行第一个数据 99 LinePD[0] = IM_ClampToByte(LastSum * Inv); 100 for (int X = 1; X < Width; X++) 101 { 102 int NewSum = LastSum - ColValue[X - 1] + ColValue[X + Radius + Radius]; 103 LinePD[X] = IM_ClampToByte(NewSum * Inv); 104 LastSum = NewSum; 105 } 106 } 107 } 108 else if (Channel == 3) 109 { 110 111 } 112 else if (Channel == 4) 113 { 114 115 } 116 free(ColValue); 117 free(ColOffset); 118 return IM_STATUS_OK; 119 }
以前没意识到,就这么简单的代码用C写后能产生速度也是很诱人的,3000*2000的图能做到39ms,如果在编译选项里勾选编译器的“启用增强指令集:流式处理 SIMD 扩展 2 (/arch:SSE2)”, 则系统会对上述具有浮点计算的部分使用相关的SIMD指令优化,如下图所示:
这个时候3000*2000的图能做到25ms,,基本上接近我改进的OPENCV的代码的速度了。
简单的描述下各函数的作用先。
IM_GetMirrorPos函数主要是得到某一个位置Pos按照镜像的方式处理时在Length方向的坐标,这里Pos可以为负值,这个主要是用来获得后期的坐标偏移的。
FillLeftAndRight_Mirror_C主要是用来获取两边镜像数据的(直接获取,不调用IM_GetMirrorPos函数),比如比如Array原始数据为 ***abcdefgh*** (Length = 8, Radius = 3),则结果为dcbabcdefghgfe。
SumofArray_C主要是计算一个数组的所有的元素的和。
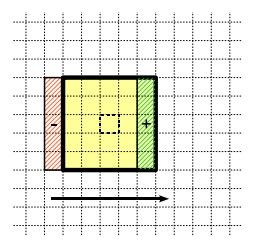
IM_BoxBlur_C函数内部即为模糊的函数体,采用的优化思路整体和任意半径中值滤波(扩展至百分比滤波器)O(1)时间复杂度算法的原理、实现及效果是一致的。当半径为R时,方框模糊的值等于以某点为中心,左右上下各扩展R像素的的范围内所有像素的综合,像素总个数为(2*R+1)*(2*R+1)个,当然我们也可以把他分成(2*R+1)列,每列有(2*R+1)个元素本例的优化方式我们就是把累加数据分成一列一列的,充分利用重复信息来达到速度提升。
我们定义一个Radius + Width + Radius的内存数据ColValue,用来保存列方向的累加数据,对于第一行数据,需要做特殊处理,也就是用原始的方式计算一行像素所有元素在列方向上的和,
详见78至于86行代码,当然这里只计算了中间Width范围内的数据,当不是第一行时,如下图左边所示,新的累加值只需减去移出的哪一行像素值同时加上移入的一行像素值,详见90到96
行代码。
上面只计算了中间Width范围内的累加值,为了方便后续代码的编写以及使用SSE优化,下面的FillLeftAndRight_Mirror_C主要作用就是填充左边和右边分别填充数据,而且是按照镜像的方式进行填充。
在更新了上述累加值后,我们开始处理计算均值了,对于每行的第一个点,SumofArray_C计算了前2*R + 1个列的累加值,这个累加值就是该点周边(2*R+1)*(2*R+1)个元素的累积和,对于一行的其他像素,其实就类似于行方向列累加值的更新,减去移出的加入新进的列,如下图右侧图所示,102到104行即实现了该过程。
原理基本上就是这样,这个算法占用的额外内存很明显很少,但是不支持In-Place操作。
为了追求速度,我们把整个过程能用SSE优化的地方都用SSE优化。
首先是第79至86行的数据,这个很容易优化:
for (int Z = -Radius; Z <= Radius; Z++) { unsigned char *LinePS = Src + ColOffset[Z + Radius] * Stride; int BlockSize = 8, Block = Width / BlockSize; for (int X = 0; X < Block * BlockSize; X += BlockSize) { int *DestP = ColValue + X + Radius; __m128i Sample = _mm_cvtepu8_epi16(_mm_loadl_epi64((__m128i *)(LinePS + X))); _mm_storeu_si128((__m128i *)DestP, _mm_add_epi32(_mm_loadu_si128((__m128i *)DestP), _mm_cvtepi16_epi32(Sample))); _mm_storeu_si128((__m128i *)(DestP + 4), _mm_add_epi32(_mm_loadu_si128((__m128i *)(DestP + 4)), _mm_unpackhi_epi16(Sample, _mm_setzero_si128()))); } // 处理剩余不能被SSE优化的数据 }
用_mm_loadl_epi64加载8个字节数据到内存,并用_mm_cvtepu8_epi16将其转换为16位的__m128i变量,后面再把低4位和高4位的数据分别转换成32位的,然后用_mm_add_epi32累加,注意后面我转换函数用了两种不同的方式,因为这里的数据绝对都是正数,因此也是可以使用_mm_cvtepi16_epi32和_mm_unpackhi_epi16组合Zero实现。
再来看看92到95行代码,这个也很简单。
int BlockSize = 8, Block = Width / BlockSize; __m128i Zero = _mm_setzero_si128(); for (int X = 0; X < Block * BlockSize; X += BlockSize) { int *DestP = ColValue + X + Radius; __m128i MoveOut = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(RowMoveOut + X)), Zero); __m128i MoveIn = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(RowMoveIn + X)), Zero); __m128i Diff = _mm_sub_epi16(MoveIn, MoveOut); // 注意这个有负数也有正数的,有负数时转换为32位是不能用_mm_unpackxx_epi16体系的函数 _mm_storeu_si128((__m128i *)DestP, _mm_add_epi32(_mm_loadu_si128((__m128i *)DestP), _mm_cvtepi16_epi32(Diff))); _mm_storeu_si128((__m128i *)(DestP + 4), _mm_add_epi32(_mm_loadu_si128((__m128i *)(DestP + 4)), _mm_cvtepi16_epi32(_mm_srli_si128(Diff, 8)))); } // 处理剩余不能被SSE优化的数据
这里也是一次性处理8个像素,这里我使用了另外一种转换技巧来把8位转换为16位,但是后面的Diff因为有正有负,要转换为32位就必须使用_mm_cvtepi16_epi32来转换,不能用unpack系列组合函数来实现,因为unpack不会移动符号位,我在这里吃了好几次亏了。
接着是FillLeftAndRight_Mirror_C函数的优化,改写如下:
void FillLeftAndRight_Mirror_SSE(int *Array, int Length, int Radius) { int BlockSize = 4, Block = Radius / BlockSize; for (int X = 0; X < Block * BlockSize; X += BlockSize) { __m128i SrcV1 = _mm_loadu_si128((__m128i *)(Array + Radius + Radius - X - 3)); __m128i SrcV2 = _mm_loadu_si128((__m128i *)(Array + Radius + Length - X - 5)); _mm_storeu_si128((__m128i *)(Array + X), _mm_shuffle_epi32(SrcV1, _MM_SHUFFLE(0, 1, 2, 3))); _mm_storeu_si128((__m128i *)(Array + Radius + Length + X), _mm_shuffle_epi32(SrcV2, _MM_SHUFFLE(0, 1, 2, 3))); } // 处理剩余不能被SSE优化的数据 }
镜像就是倒序的过程,直接使用SSE的shuffle函数很方便实现。
计算数组的累加和优化也方便。
int SumofArray_SSE(int *Array, int Length) { int BlockSize = 8, Block = Length / BlockSize; __m128i Sum1 = _mm_setzero_si128(); __m128i Sum2 = _mm_setzero_si128(); for (int X = 0; X < Block * BlockSize; X += BlockSize) { Sum1 = _mm_add_epi32(Sum1, _mm_loadu_si128((__m128i *)(Array + X + 0))); Sum2 = _mm_add_epi32(Sum2, _mm_loadu_si128((__m128i *)(Array + X + 4))); } int Sum = SumI32(_mm_add_epi32(Sum1, Sum2)); // 处理剩余不能被SSE优化的数据 return Sum; }
使用两个__m128i 变量主要是为了充分利用XMM寄存器,其中SumI32函数如下,主要是为了计算__m128i 内四个整数的累加值。
// Convert 4 32-bit integer values to 4 unsigned char values.
void _mm_storesi128_4char(__m128i Src, unsigned char *Dest) { __m128i T = _mm_packs_epi32(Src, Src); T = _mm_packus_epi16(T, T); *((int*)Dest) = _mm_cvtsi128_si32(T); }
代码不解释。
最后就是100到104行的代码的转换。
int BlockSize = 4, Block = (Width - 1) / BlockSize; __m128i OldSum = _mm_set1_epi32(LastSum); __m128 Inv128 = _mm_set1_ps(Inv); for (int X = 1; X < Block * BlockSize + 1; X += BlockSize) { __m128i ColValueOut = _mm_loadu_si128((__m128i *)(ColValue + X - 1)); __m128i ColValueIn = _mm_loadu_si128((__m128i *)(ColValue + X + Radius + Radius)); __m128i ColValueDiff = _mm_sub_epi32(ColValueIn, ColValueOut); // P3 P2 P1 P0 __m128i Value_Temp = _mm_add_epi32(ColValueDiff, _mm_slli_si128(ColValueDiff, 4)); // P3+P2 P2+P1 P1+P0 P0 __m128i Value = _mm_add_epi32(Value_Temp, _mm_slli_si128(Value_Temp, 8)); // P3+P2+P1+P0 P2+P1+P0 P1+P0 P0 __m128i NewSum = _mm_add_epi32(OldSum, Value); OldSum = _mm_shuffle_epi32(NewSum, _MM_SHUFFLE(3, 3, 3, 3)); // 重新赋值为最新值 __m128 Mean = _mm_mul_ps(_mm_cvtepi32_ps(NewSum), Inv128); _mm_storesi128_4char(_mm_cvtps_epi32(Mean), LinePD + X); }
以前认为这个算法难以使用SSE优化,主要难处就在这里,但是在学习了Opencv的积分图技术时,这个问题就迎刃而解了,进一步分析还发现Opencv的代码写的并不完美,还有改进的空间,见上述代码,使用两次对同一数据移位就可以获取累加,由P3 P2 P1 P0变为P3+P2+P1+P0 P2+P1+P0 P1+P0 P0。我们稍微分析一下。
__m128i ColValueDiff = _mm_sub_epi32(ColValueIn, ColValueOut); 这句代码得到了移入和移出序列的差值,我们计为; P3 P2 P1 P0 (高位到低位)由于算法的累加特性,如果说OldSum的原始值为A3 A3 A3 A3,那么新的NewSum就应该是:
A3+P3+P2+P1+P0 A3+P2+P1+P0 A3+P1+P0 A3+P0;
__m128i Value_Temp = _mm_add_epi32(ColValueDiff, _mm_slli_si128(ColValueDiff, 4)); 这句的_mm_slli_si128得到中间结果 P2 P1 P0 0, 再和P3 P2 P1 P0相加得到
Value_Temp = P3+P2 P2+P1 P1+P0 P0
__m128i Value = _mm_add_epi32(Value_Temp, _mm_slli_si128(Value_Temp, 8));这句的_mm_slli_si128得到中间结果P1+P0 P0 0 0,再和P3+P2 P2+P1 P1+P0 P0相加得到:
Value = P3+P2+P1+P0 P2+P1+P0 P1+P0 P0
好简单的过程。
OldSum = _mm_shuffle_epi32(NewSum, _MM_SHUFFLE(3, 3, 3, 3)); 这一句为什么要这样写,恐怕还是读者自己体会比较好,似乎不好用文字表达。
最后一个_mm_storesi128_4char是我自己定义的一个将1个__m128i里面的4个32位整数转换为字节数并保存到内存中的函数,详见附件代码。
至于24位图像的优化,是个比较尴尬的处境,因为SSE一次性处理4个32位数,而24位每个像素只有3个分量,这种情况一般还是把他扩展到4个分量,比如说ColValue就可以改成4通道的,然后累积和也需要处理成4通道的,这当然需要一定的奇巧淫技,这里我不想多谈,留点东西给自己。当然也可以考虑先把24位分解到3个灰度内存,然后利用灰度的算法进行计算,后面在合成到24位,这个分解和合成的过程也是可以使用SSE加速的,如果你结合多线程,还可以把3个灰度过程的处理并行化,这样除了多占用内存外,速度比至二级处理24位要快(因为直接处理算法无法并行的,前后依赖的缘故)。另外就是最后在计算列累积求平均值的过程也变得更加自然了,不会出现灰度那种要在__mm128i内部进行累加的过程,而是直接得两个SSE变量累加。
还说一点,现在大部分的CPU都支持AVX256了,还可以使用AVX进一步加速,似乎代码该起来也不是很难,有兴趣的朋友可以自己试试。
可以说,目前这个速度已经基本上达到了CPU的极限了,但是测试过IPP的速度,似乎比这个还要快点,不排除他使用了AVX,也不排除他使用多核的资源。
这个的优化对于BoxBlur来说是重要的一步,但是更重要的是他可以运用在很多场合,比如图像的局部均方差计算,也可以使用类似的技术进行加速,两幅图像大的局部平方差也是可以这样优化的,后续我会简单的谈下他在这方面加速的应用。
源代码下载:https://files.cnblogs.com/files/Imageshop/FastBlur.rar
彩色图工程:https://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar
不好意思,图太小,速度为0ms了。