这一次阅读,把第一卷的48个命题平均分成三个部分。每个部分16个命题。
第一部分研究相等关系,包括三边相等的三角形,两个全等的三角形,相等的线段,有两边相等的三角形,分角为相等的两部分,直线相交成相等的邻角,等。
第二部分研究不等关系和平行关系, ≠ ,不等号是这样的,研究平行线时,也是这样的,用一条斜线交两线。
第三部分研究等面积变换。
先从第三部分开始讨论,然后第一部分,最后第二部分。
因为第三部分,相对容易理解。
等幂变换
这部分的目标:化任意多边形为等面积的正方形。
内容:从第三十三命题到第四十八命题。
因为这些命题,大部分是夹在平行线之间的平行四边形以及三角形,只要预先假定
两平行线之间,距离处处相等。
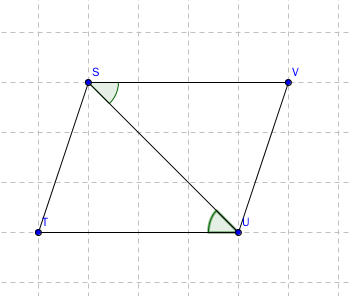
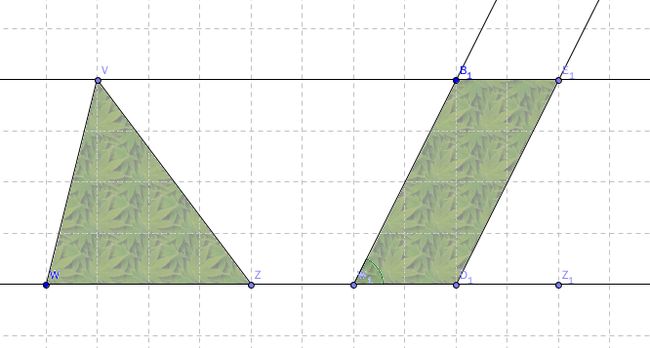
由于欧氏几何独特的性质,如图,从S点向直线TV引垂线ST,这垂线必然也垂直于直线SU。因此,可以定义平行线之间的距离。
这些距离,图中ST,UV,WZ,等,都相等。
有了这个假设,则大部分命题比较容易理解。其实,这个命题也可以作为公设,代替传说中的第五公设。这个命题与第五公设是等价的。
有了第五公设,就有了平行线的性质,这个假设也就不是假设,而是可以证明的定理。
但书中似乎没有出现“距离”这样的字样。一直用线段度量线段,就是考虑线段与线段的比值。这一点,同《九章算术》明显不同。《九章》中,(刘徽)在计算圆周率的时候,就使用了各种长度单位;在《海岛算经》中,各种长度单位的转化更是繁复。
用单位,实际上也是规定了一个固定的线段。其它来与之比例。用阿基米德原理公理,才可能完成度量。
用比例,就避免了单位的转化。相同单位的两个量一比,单位就消失了。更重要的原因是,继承了毕达哥拉斯学派的传统,一定要找到线段和线段之间的“最大公约数”,就是“可公度量”。让线段之间可以产生比。
那个时候,对比就是除法,就是分数还没有认识。这同无理数不能精确的用比例表示有关。
无理数的危机是如何解决的,等我读到那一章,再了解。
因为现在倒着看这一章书,所以先假定有“距离”这概念。
下面有几个命题,都如“等底等高的三角形面积相等”之类,这些命题中“夹在平行线间”就意味着“等高”。
命题三十三 一组对边平行且相等的四边形是平行四边形。
如图,只要有SV平行于TU,而且SV=TU,那么这个四边形就是平行四边形。
一组对边平行且相等,就能保证另一组对边也如此。
证明用到三角形全等和平行线的性质。在下一个命题中有体现。
命题三十四 平行四边形对边相等,对角相等,对角线平分该四边形。
命题三十三平行四边形的判定定理,命题三十四是性质定理。利用平行线的性质和三角形全等,容易证明。
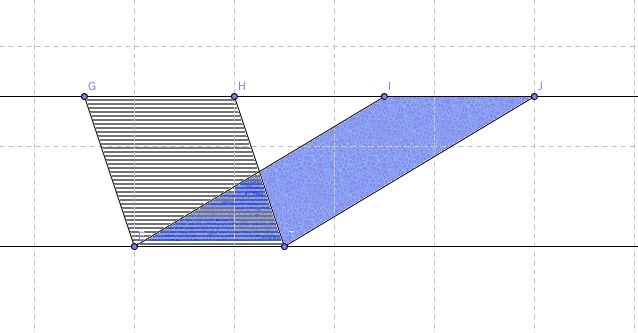
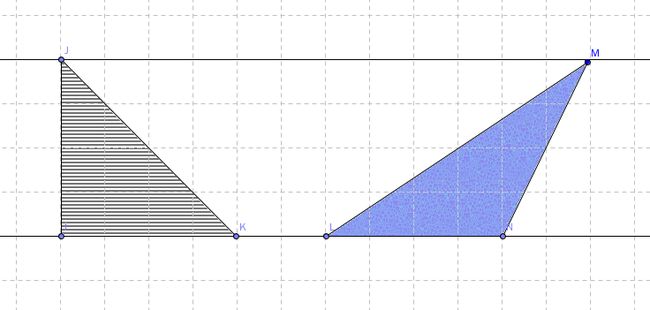
命题三十五 同底且在二平行线之间的平行四边形面积相等。
这种四边形可以看作下底不动,上底在平行线上移动,变化出的所有平行四边形面积都相等。一个特殊的位置,就是恰好为长方形的时候,面积值也一样,高与边重合。
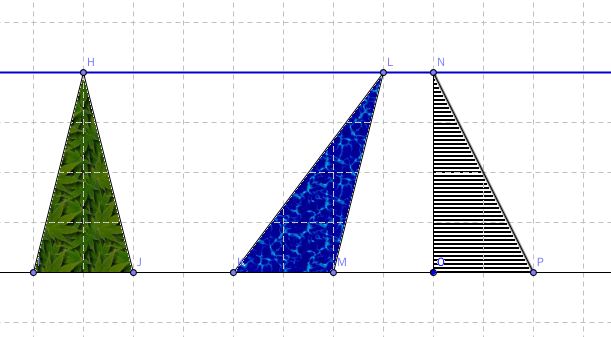
命题三十六 等底且在二平行线之间的平行四边形面积相等。
平行四边形的高也可以不在形内。高也许真的比底要高。
你一定会奇怪,这么简单的事情为什么要说两遍?现代说“等底等高的平行四边形面积相等”不就解决了?
因为,那时用几何在运算,并非用代数运算。现代用代数运算,一个公式
S=ah可表示平行四边形的面积,另一个公式S=ah/2可以表示三角形的面积。
但那时,在欧几里得之前,并没有“平行四边形是”这东西,“平行四边形”这种形状本身就是欧几里得发明的。
所以,我们不能苛求什么。
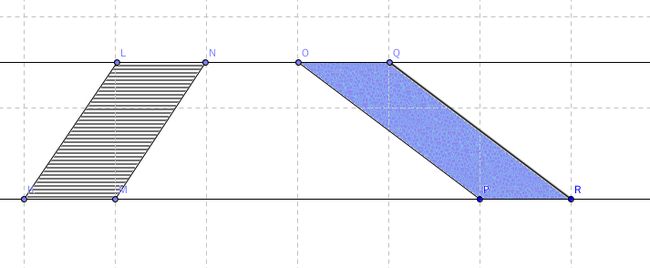
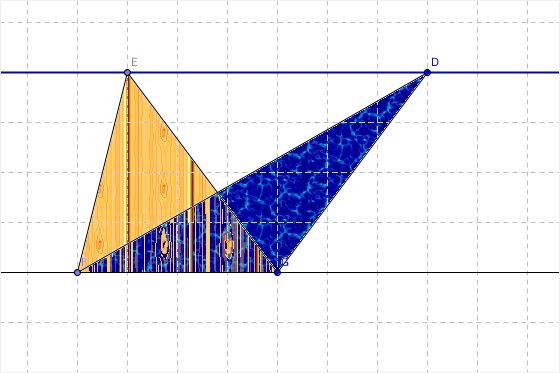
命题三十七 同底且在二平行线之间的三角形面积相等。
命题三十八 等底且在二平行线之间的三角形面积相等。
同上面两个命题一样的道理。因为每个平行四边形都可以剖分成全等的两个三角形,所以,就成立。
用面积公式:
平行四边形面积 = (底 乘以 高)
三角形面积 = (底 乘以 高) 除以 二
从图形上看,等底的情形是更普遍的。两个三角形可以平移,重合一边,就成了同底的情形。平行线的存在,保证了,绝对会等高。
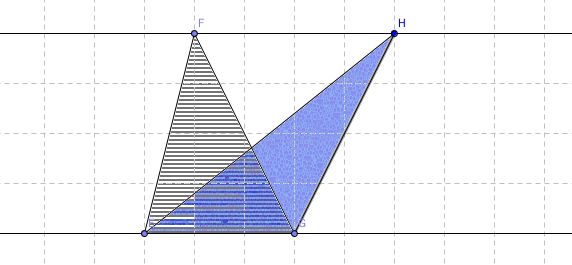
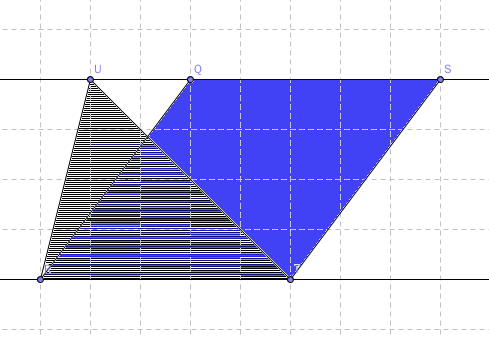
命题三十九 同底等面积,顶点位于底边同侧的三角形顶点连线平行于底边。
面积相等可以得出高相等,进而得到平行的结论。有了这个命题以后,就可以省略那些步骤了。
省略一些会比较好,因为有的时候,证明过程中,你会忘记哪个命题是先有的,哪一个是后来才有的,容易有一些颠倒因果的做法。
并非所有的角度相等都是通过三角形全等来证明的。通过SAS直接得到一个角相等,在希尔伯特体系中,是公理。然后才有SAS全等。假如先用SAS证明了全等,然后说“因为全等,所以某某角相等”,就是颠倒了因果。
这种做法就好比做一个分解因式的题目,本该提取公因式以继续,却用乘法分配律展开了,不知道在做什么,倒回去了。
命题四十 等底等面积,顶点位于底边同侧的三角形顶点连线平行于底边。
这两个命题分别是命题三十七和命题三十八的逆命题。可以利用面积证明平行。也是平行判定的一种方法。
这种证明平行的方法,要求很严格:
第一,所有三角形的底边共一条直线;
第二,所有三角形在平面上直线的同侧;
第三,所以三角形面积相等;
第四,所有三角形底边一样长。
因为要求这么严格,很少有机会同时满足,所以,我记忆中没有使用过。
但看来很强大,不但可以证明平行,如果结合Playfair公理,简直可以证明3点共线、4点共线直到100点共线。
实际中也许不容易构造这样的三角形。下一次遇到证明共线的题目,一定要尝试一下构造满足上述四个条件的三角形。
命题四十一 夹在平行线间的平行四边形和三角形,如果同底,则平行四边形面积是三角形的两倍。
这是为本书中为证明勾股定理专门做的铺垫定理。
后面很少出现。
命题四十二 给定平行四边形一角,可作平行四边形面积等于已知三角形的面积。
这两个命题就是:保证面积不变,化三角形的平行四边形的理论依据。
既然等底等高的平行四边形面积是三角形的两倍,那么,如果要把三角形化作面积相等的平行四边形,只需要底边折半。
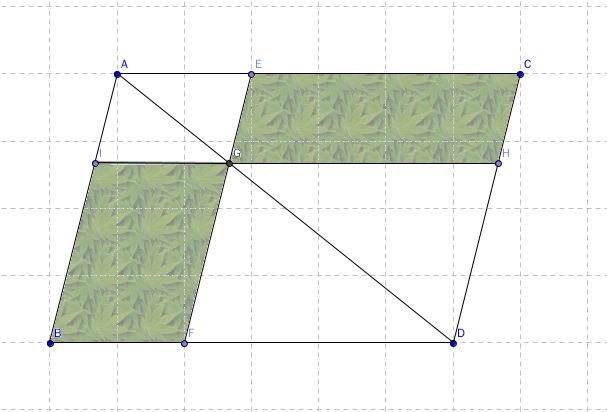
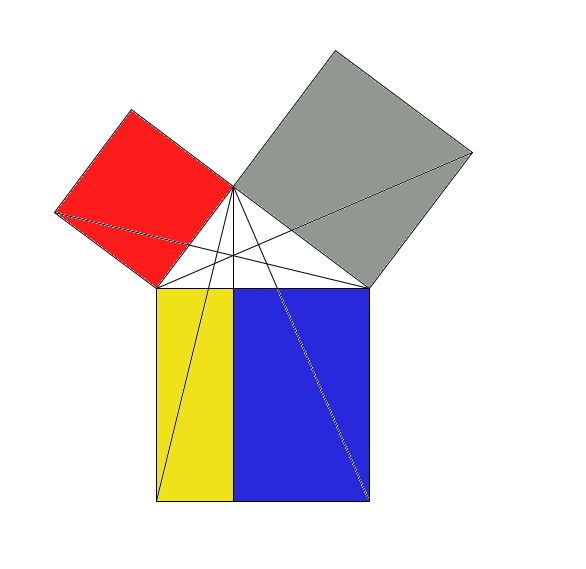
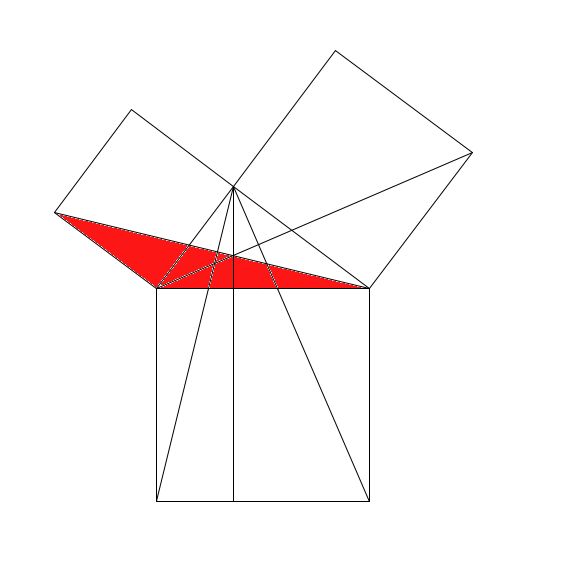
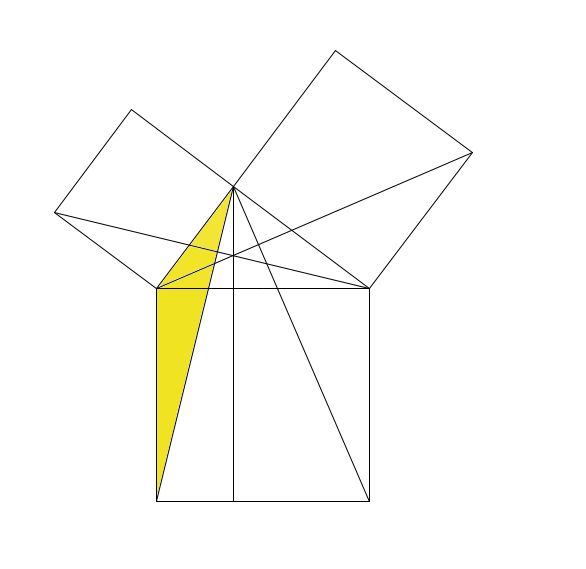
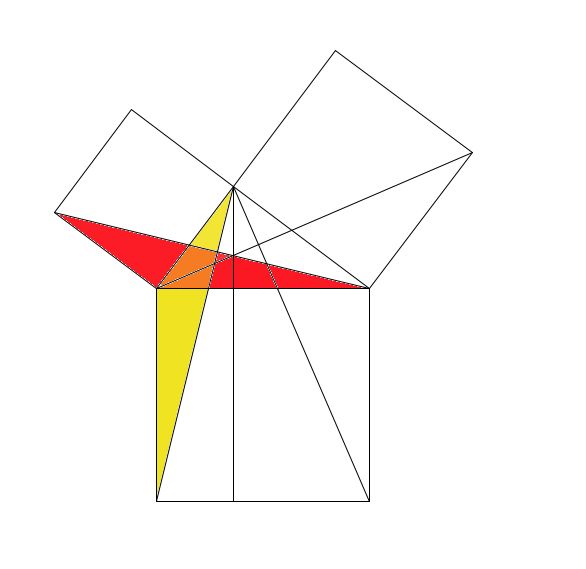
命题四十三 对角线两边的补形面积相等。
这里,定义了一种特殊的形状,叫“补形”,就是从平行四边形对角线上一点,引边的平行线,得到对角线两侧的平行四边形。就是图中有背景的两个平行四边形。通过全等的部分减去全等的部分证明:对角线AD分平行四边形为全等的两部分ABD和ACD,两部分中,没有着色的三角形也分别相等,因此,减去相等的部分以后,得到补形,仍然相等。
这个命题提供了一种方法,可把一个平行四边形改装成另一个,面积不变。
正是因为“补形”的存在,才需要画图的。不画图,实在是很难表达清楚。
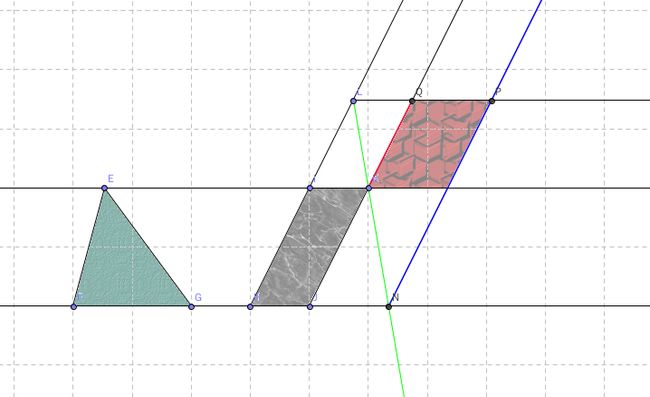
命题四十四 给定平行四边形一角和一边,可作平行四边形面积等于已知三角形的面积。
这个命题合并了命题四十二和四十三的结果,可以作出指定一角和一边的平行四边形。如果指定这个角为直角,那么,就可以把三角形化为矩形。
先按照按照命题四十二的方法作给定角度的平行四边形,等于已知三角形面积。然后,向上延长两边,延长的长度是给定的(红色为延长的长度)。得到大平行四边形的一个顶点。再作出图中绿色的对角线,对角线与下底所在直线有交点,这个交点作为大平行四边形的第三个定点。
最后作蓝色平行线,确定大四边形的第四个顶点。
同时,作出了相等的补形。
命题四十五 给定平行四边形一角,可以做平行四边形面积等于已知多边形。
方法:先把多边形沿着一个顶点引出的对角线,割成一个一个的三角形,用上一个命题的方法,可以作出给定一边和一角的一个一个平行四边形。因为先固定一边和一角,这些平行四边形可以很好的拼接在一起,形成一个长长的平行四边形。如果最初指定一角是直角,那么作出的是矩形。
至此,任意的多边形都可以转化为等面积的平行四边形(或矩形)。
命题四十六 给定边长,可作正方形。
这个命题与上一个命题之间,留下一些空白。那就是:作一个正方形,面积等于已知的长方形。这个空白将在第二卷的命题十四得到填补。
是第一命题的后续。
第一命题做正三角形,这里做正方形,未来的章节还有正五边形,正六边形等。也就是说,能用尺规作图做出的正多边形,都会出现。
作正方形,仅仅只是为了延续“正多形序列”,展示几何的美感,没有别的意思。作为尺规作图能作出的正多边形的一种,给人的感觉是方方正正。
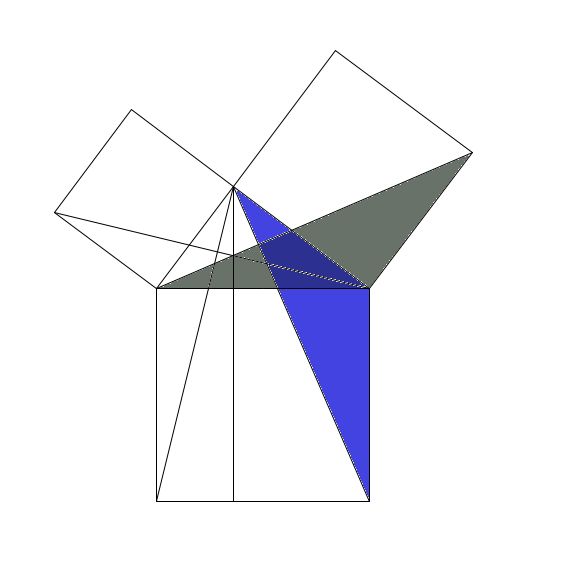
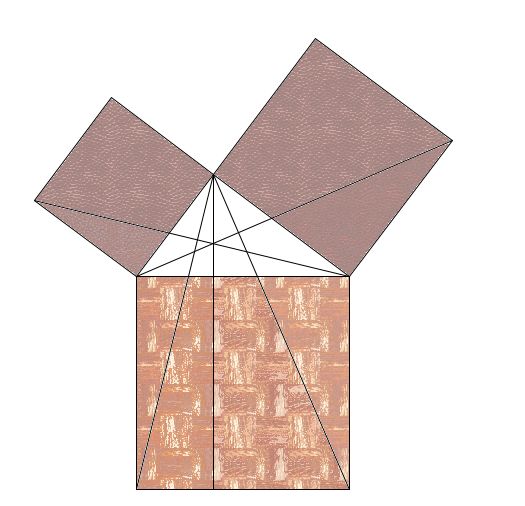
命题四十七 勾股定理
将已知两正方形合并为等面积的一个正方形。
这个就是压轴的勾股定理。证明的时候用到了平行线的性质,上面的各种面积相等,以及简单的三角形全等SAS。这个证明精妙绝伦。
如果把证明过程中用的图,着上颜色,会像孔雀开屏。
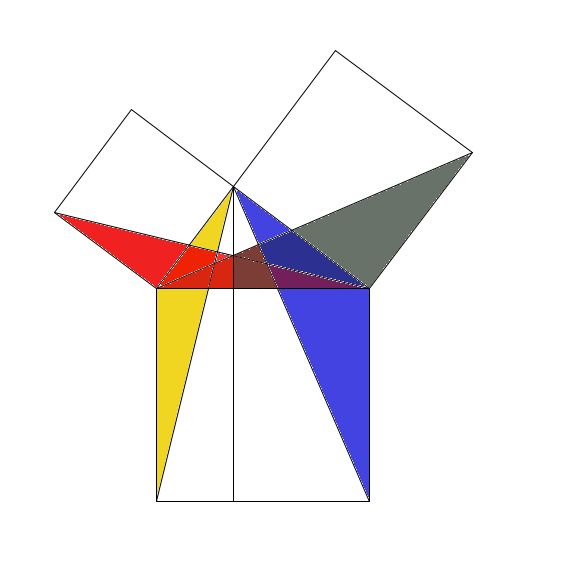
先延长中间的白色直角三角形斜边上的高,把下面的正方形分成黄色和蓝色两个部分。
然后,
黄色的部分用黄药师代替,
蓝色的部分用南帝代替,
原来直角三角形肩膀上的两个小正方形:
红色的用洪七公代替,
灰色的用欧阳锋代替。
比武的规则是:
黄药师与蓝帝联手,对抗
红七公与灰色的欧阳锋联手。
大宗师一般都不直接比武,于是排出各自的弟子。
鲁有脚的功夫正好是洪七公的五成。
梅超风的功力也正好是黄药师的五成。
梅超风和鲁有脚迫不及待的进行了第一场比武,正好平手。
(这两个三角形全等,用SAS证明。旋转90度,刚好可以重合。)
这就从侧面印证了,黄药师和洪七公的功力一样。
同时进行的还有,第二场比武,由欧阳克代表欧阳锋,由武三通代表南帝:
这两位的功力也恰好是各自师父的一半,这两位也恰好打平手。印证了,南帝的功力和老毒物一样。
两场比武都是平手,所以
黄药师 + 南帝 = 洪七公 + 老毒物
因此,在华山论剑中(在直角三角中),
黄药师和南帝方阵(斜边上的正方形面积)与
洪七公和老毒物葫芦阵(两直角边上的正方形面积之和)
战平(相等)。
真实比武的场面是这样的。
有人说像风车,有人说像孔雀开屏。
我从这里看到大宗师的手笔。
在直角三角形中,斜边上的正方形面积等于两直角边上正方形面积之和。
命题四十八 勾股定理逆定理
证明:略
用途:利用面积,可以证明垂直。
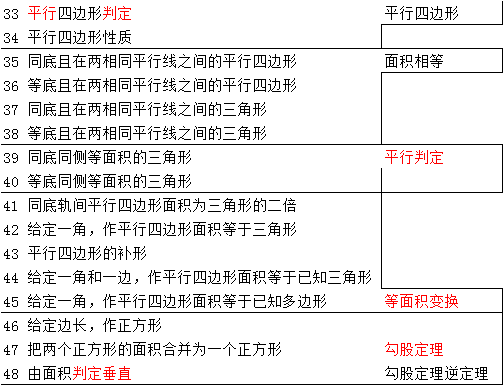
第三部分全部内容
整理如下
这部分的目标是:化任意多边形为等面积的正方形。逻辑是顺序推理的,只跳跃了“化长方形为正方形”的步骤。除了跳跃的一个步骤(跳跃的步骤在第二卷第十四命题得到补充),所有任务都已完成。
实际上,初一整整一个上学期的几何,内容相当于第一卷的四十八个命题。
一方面,学习几何语言,诸如“取直线 l 外一点P”之类;
一方面,学习证明的逻辑,书写的格式,三段论和反证法;
还有一方面,就是不断的练习,熟悉题目,以应对考试。
计划为这四十八个命题,各挑选一句古诗词,来装饰一下。几何的美太朴素,太单纯。至少两个命题共用一联。
自写的打油诗不美观,但好记忆。下回分解。