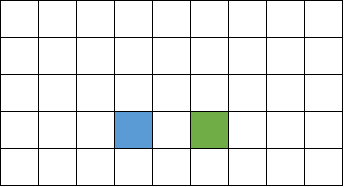昨天的大概就咕咕咕了
今天说差分
多图预警
于是,进入正题
今天的主题是差分
但我们或许也应该先说说前缀和
众所周知,差分是前缀和的逆运算
跟我一起念三遍:
差分是前缀和的逆运算,差分是前缀和的逆运算,差分是前缀和的逆运算,差分是前缀和的逆运算
打了四遍(皮)
于是就有了前缀和维护差分和差分维护前缀和
我们先考虑一维差分
给你一个数列num,有n项,每次操作对一段区间加上一个数或减去一个数,最后询问数列中的各个元素是多少
要求做到$\Theta (操作数+数组大小)$
我们发现只有一次询问
所以可以差分
维护一个数组a[i],a[i]意义为num[i]比num[i+1]大多少
易得区间加操作只会改变 区间左端点-1 和 区间右端点 的a值
最后只需要求a[i]的前缀和(上面说过差分是前缀和的逆运算)就好了
于是这道题就被切了
下面我们把数列扩展到二维
先考虑二位前缀和
在这张图中,黑点的意义为下图黑色区域的值的和
也就是左上区域
考虑怎么求出这个值
显然可以由上面的格子的前缀和与左面的格子的前缀和加和得到
但是这样的话,下图中的黑色区域会被计算两次
明显算多了
那么就减去它,即:
a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]
那么考虑差分
始终记住一句话:差分是前缀和的逆运算
我们考虑对于一个点,那些点的差分值对它有贡献
对于下图中的黑点
下图中的黑色部分都可以对它产生贡献
那么假如我们希望让下图的黑色区域的值都加一
我们可以让下图的黑色点的差分值加一
这样
黑色部分就全都加了1
但是我们明显加多了
黑色部分都被多加了1
那就减掉!
于是我们又把这两个黑点的差分值-1
好像OK了?
然而
细心的你应该会发现
我们把下图中的点多减了1
那么我们再
把这个黑点的差分值加1
这样就对了吧
ok,让我们捋一捋
我们先简单粗暴地把左上角的差分值加1
但发现加多了
于是有把加多的部分减掉了
又发现减多了
于是又把减多的加上了
加---减---加
这就是二维差分的方法
明白了?现在进入hard模式
考虑在二维情况下的三角差分
对,我们要把形如下图的部分加1
思考一下*1
思考一下*2
思考一下*3
思考一下*4
思考一下*5
思考一下*6
思考一下*7
思考一下*8
思考一下*9
思考一下*10
思考时间到了!!!
接下来公布思路:
我们仍然需要四边形的差分,但要再引入一个三角形的差分
在这个新的差分中
下图黑点的作用范围将是下下张图
变成三角了有目有
考虑如何加1
我们可以先在黑点处加一
那我们就会将下图的黑色区域加一
于是我们加多了对吧
参照刚刚的总结
接下来我们该减了
但我们加多的区域是一个梯形
显然不是只用三角形可以维护的
但是这是个直角梯形
还能被拆成一个四边形+一个三角形
于是我们可以将蓝色点的四边形的差分-1,绿色点的三角形差分-1(终于不是黑白双色的图了)
于是我们这次减多了
黑色部分被多减了1(又变成黑白双色的图了)
那就加1
于是,完结!!!