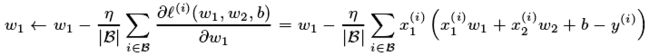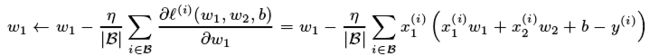一、线性回归---单层神经网络

1、简单介绍

线性回归模型为，其中w₁和w₂为对应特征x_1、x₂的权重，b为偏差。

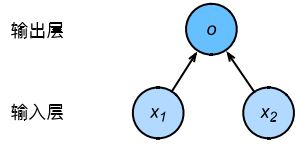
用神经网络图表现线性回归模型如下，图中未展示权重和偏差：

输入层为x_1、x₂，输入层个数为2，在神经网络中输入层个数即为特征数。输出为o，输出层个数为1.，即为线性回归模型中的输出。由于输入层不参与计算，计算层仅有输出层一层，故神经网络层数为1，即线性回归是一个单层神经网络。神经网络中负责计算的单元叫神经元，在该模型中o即为神经元。在线性回归中，o的输出依赖于x_1、x₂，即输出层中的神经元和输入层中各个输入完全连接，故，此处输出层又叫全连接层。

2、线性回归的实现

（1）一些概念

（1.1）np.random.normal(size,loc,scale)

loc：此概率分布的均值（对应着整个分布的中心centre），不写默认为0

scale：此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高），方差=标准差的平方

size：输出的shape，默认为None，只输出一个值

（1.2）矩阵乘法

X*X^T表示如下

nd.dot(X, X.T)

（1.3）自动求梯度

函数：y = 2x^TX求列向量x的梯度

（a）求变量x的梯度，需要先调用attach_grad函数来申请存储梯度所需要的内存

x.attach_grad()

（b）mxnet需要调用record函数来记录与梯度有关的计算

with autograd.record():

　　y = 2 * nd.dot(x.T, x)

（c）调用backward函数自动求梯度，如果y不是一个标量，mxnet将会先对y中元素求和得到新的变量，再求该变量有关x的梯度

y.backward()

（d）获取变量x的梯度结果

x.grad

（1.4）小批量随机梯度下降迭代模型参数

线性回归中模型参数迭代过程如下：

w₁是迭代的参数，η是学习率取正数，是小批量中的样本个数

（2）实现过程

（2.1）生成数据集

构造一个训练数据集，样本数为1000，特征数为2。随机批量生成样本1000*2，使用线性回归模型真实权重W=[2,-3.4]^T和偏差b=4.2，以及一个随机噪声e来生成标签，数据之间的关系为y=XW+b+e，其中噪声e服从均值为0，标准差为0.01的正态分布。

from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd,nd
import random
num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 4.2
features = nd.random.normal(scale=1,shape=(num_examples,num_inputs))
labels = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
labels += nd.random.normal(scale=0.01,shape=labels.shape)

（2.2）生成小批量

在多次迭代模型参数时，每次迭代中，根据当前读取的小批量数据样本，通过调用反向函数backward计算小批量随机梯度，并调用优化算法sgd迭代模型参数。小批量函数每次返回一个batch_size大小的随机样本及标签

# 读取小批量，每次返回一个batch_size大小的随机样本及其标签
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)#样本读取顺序随机
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i:min(i + batch_size, num_examples)])
        yield features.take(j),labels.take(j)

（2.3）线性回归矢量计算

矢量计算公式y=X*w+b，dot函数可以用来做矩阵乘法

# 线性回归矢量计算表达式，用dot函数做矩阵乘法
def linreg(X, w, b):
    return nd.dot(X,w) + b

（2.4）定义损失函数

线性回归采用平方损失函数来计算损失，输入为值为模型预测出来的标签和真实标签，在计算过程中其中两个标签的形状不一样，需要进行转换

# 定义损失函数
# 将真实值y变成预测值y_hat的形状，以便进行平方损失的计算
def squared_loss(y_hat,y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

（2.5）迭代模型参数，优化损失函数

 params是传入的需要迭代的参数，此处为w和b，lr为学习率此处自定义为0.03，batch_size为自定义小批量样本大小，采用迭代公式为下图

此处，对于一个迭代周期中，小批量样本迭代选择参数过程中，直接取的一个迭代周期中最后一个小批量对应的参数

def sgd(params, lr, batch_size):
    for param in params:
        param[:] = param - lr * param.grad / batch_size

（2.6）完整代码

部分说明：在每一个迭代周期中，将会完整遍历一遍所有数据，迭代小批量求出最佳模型参数，然后根据最佳参数得出训练数据集的损失值

from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random
from IPython import display
import d2lzh as dlz

num_inputs = 2  # 指定输入特征个数
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
# 权重初始化为均值为0，标准差为0.01的正态随机数，偏差初始化为0
w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))
# 在模型训练中迭代w和b，因此要创建它们的梯度
w.attach_grad()
b.attach_grad()
# 在每次迭代中
lr = 0.03
num_epochs = 3
net = dlz.linreg
batch_size = 10
# 迭代周期
for epoch in range(num_epochs):
    # 在每个迭代周期中会使用训练数据集中所有的样本
    # 小批量迭代寻找每次迭代周期中最佳参数
    for X, y in dlz.data_iter(batch_size, features, labels):
        with autograd.record():
            l = dlz.squared_loss(net(X, w, b), y) # l是有关小批量X和y的损失
        l.backward() # 小批量的损失对模型参数求梯度
        dlz.sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
    train_l = dlz.squared_loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))
'''
输出结果：
epoch 1, loss 0.035021
epoch 2, loss 0.000126
epoch 3, loss 0.000048
'''