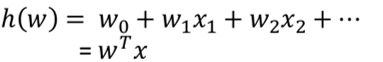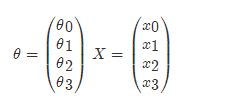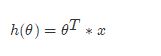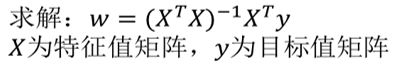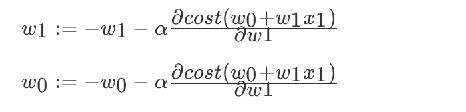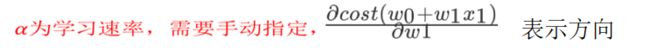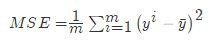目录
- 损失函数
- 正规方程
- 梯度下降
- sklearn线性回归正规方程、梯度下降API
- 回归性能评估
- sklearn回归性能评估
- 欠拟合与过拟合
- 解决过拟合的方法
- L2正则化
线性回归的定义是:目标值预期是输入变量的线性组合。线性模型形式简单、易于建模,但却蕴含着机器学习中一些重要的基本思想。线性回归,是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
单变量线性回归:涉及到的变量只有一个。例如:预测房价例子中房子的大小预测房子的价格。f(x) = w1*x+w0,这样通过主要参数w1就可以得出预测的值。通用公式为:
多变量线性回归:涉及到的变量两个或者两个以上。例如:瓜的好坏程度 f(x) = w0+0.2色泽+0.5根蒂+0.3*敲声
,得出的值来判断一个瓜的好与不好的程度。通用公式为:
线性回归的通用公式如下:
线性模型中的向量W值,客观的表达了各属性在预测中的重要性,因此线性模型有很好的解释性。对于这种“多特征预测”也就是(多元线性回归),那么线性回归就是在这个基础上得到这些W的值,然后以这些值来建立模型,预测测试数据。简单的来说就是学得一个线性模型以尽可能准确的预测实值输出标记。
那么如果对于多变量线性回归来说我们可以通过向量的方式来表示W值与特征X值之间的关系:
两向量相乘,结果为一个整数是估计值,其中所有特征集合的第一个特征值x_0x0=1,那么我们可以通过通用的向量公式来表示线性模型:
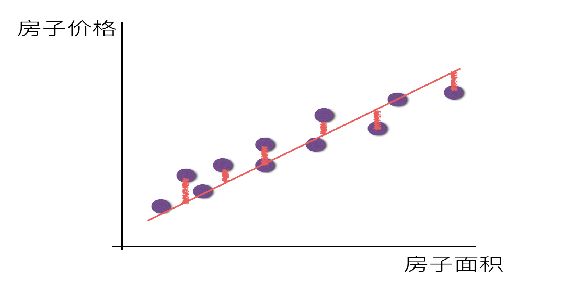
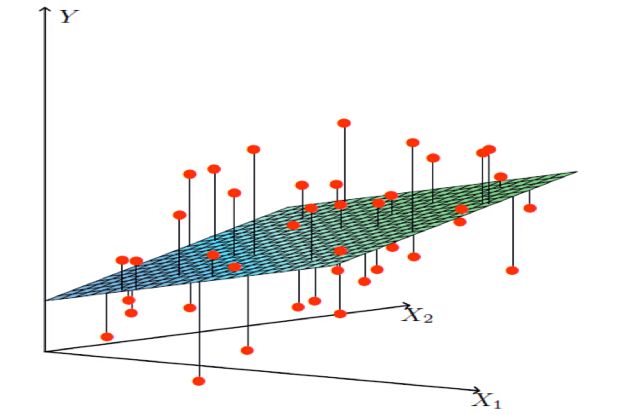
一个列向量的转置与特征的乘积,得出我们预测的结果,但是显然我们这个模型得到的结果可定会有误差,如下图所示:
单变量:
多变量:
损失函数
损失函数是一个贯穿整个机器学习重要的一个概念,大部分机器学习算法都会有误差,我们得通过显性的公式来描述这个误差,并且将这个误差优化到最小值。
对于线性回归模型,将模型与数据点之间的距离差之和做为衡量匹配好坏的标准,误差越小,匹配程度越大。我们要找的模型就是需要将f(x)和我们的真实值之间最相似的状态。于是我们就有了误差公式,模型与数据差的平方和最小(最小二乘法):
上面公式定义了所有的误差和,那么现在需要使这个值最小?那么有两种方法,一种使用梯度下降算法,另一种使正规方程解法(只适用于简单的线性回归)。
单变量损失函数直观图:
正规方程
缺点:当特征过于复杂时,求解速度太慢。
对于复杂的算法,不能使用正规方程求解。
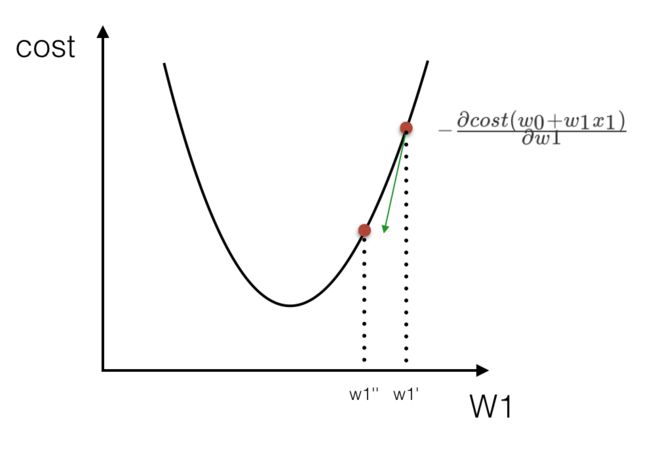
梯度下降
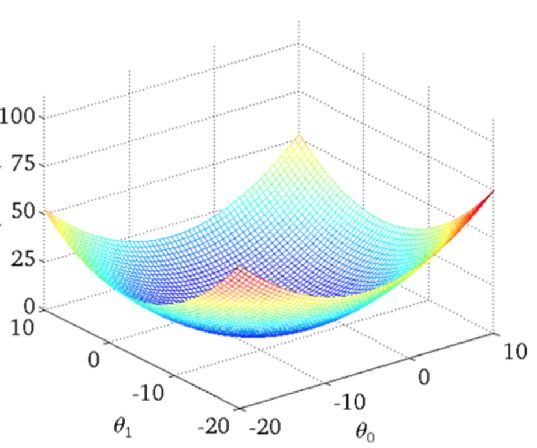
我们以单变量中的w0,w1为例子:
理解:沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新W值
sklearn线性回归正规方程、梯度下降API
sklearn.linear_model.LinearRegression()
- 普通最小二乘线性回归
- coef_:回归系数
sklearn.linear_model.SGDRegressor( )
- 通过使用SGD最小化线性模型
- coef_:回归系数
波士顿房价预测:
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor
lb = load_boston()
# 分隔数据集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 特征工程-标准化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 正则方程求解预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print(lr.coef_)
# 预测的价格
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
print("使用正规方程每个房子的预测价格:", y_lr_predict)
# 使用梯度下降进行预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print(lr.coef_)
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
print("使用梯度下降预测的房子价格:", y_sgd_predict)回归性能评估
对于不同的类别预测,我们不能苛刻的要求回归预测的数值结果要严格的与真实值相同。一般情况下,我们希望衡量预测值与真实值之间的差距。因此,可以测评函数进行评价。其中最为直观的评价指标均方误差(Mean Squared Error)MSE,因为这也是线性回归模型所要优化的目标。
MSE的计算方法如下:
sklearn回归性能评估
mean_squared_error(y_true, y_pred)
- 均方误差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果
对于前面预测波士顿房价的例子,对其回归性能进行评估:
from sklearn.metrics import mean_squared_error
...
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
...
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))结果:
正规方程的均方误差: 25.14886868419582
梯度下降的均方误差: 25.962570579781715欠拟合与过拟合
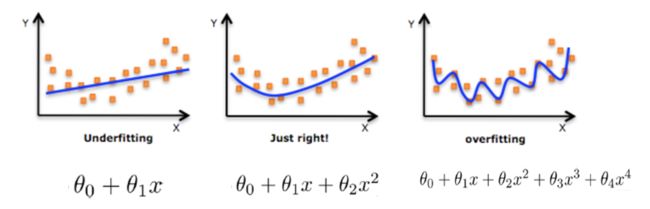
机器学习中的泛化,泛化即是,模型学习到的概念在它处于学习的过程中时模型没有遇见过的样本时候的表现。在机器学习领域中,当我们讨论一个机器学习模型学习和泛化的好坏时,我们通常使用术语:过拟合和欠拟合。我们知道模型训练和测试的时候有两套数据,训练集和测试集。在对训练数据进行拟合时,需要照顾到每个点,而其中有一些噪点,当某个模型过度的学习训练数据中的细节和噪音,以至于模型在新的数据上表现很差,这样的话模型容易复杂,拟合程度较高,造成过拟合。而相反如果值描绘了一部分数据那么模型复杂度过于简单,欠拟合指的是模型在训练和预测时表现都不好的情况,称为欠拟合。
欠拟合例子:
经过训练后,知道了天鹅是有翅膀的,天鹅的嘴巴是长长的。简单的认为有这些特征的都是天鹅。因为机器学习到的天鹅特征太少了,导致区分标准太粗糙,不能准确识别出天鹅。
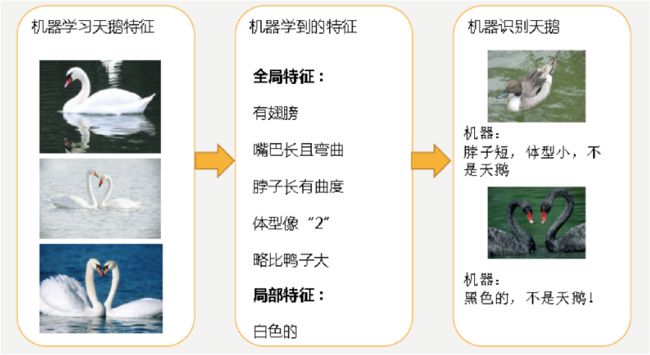
过拟合例子:
机器通过这些图片来学习天鹅的特征,经过训练后,知道了天鹅是有翅膀的,天鹅的嘴巴是长长的弯曲的,天鹅的脖子是长长的有点曲度,天鹅的整个体型像一个"2"且略大于鸭子。这时候机器已经基本能区别天鹅和其他动物了。然后,很不巧已有的天鹅图片全是白天鹅的,于是机器经过学习后,会认为天鹅的羽毛都是白的,以后看到羽毛是黑的天鹅就会认为那不是天鹅。
过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合:一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
对线性模型进行训练学习会变成复杂模型:
解决过拟合的方法
在线性回归中,对于特征集过小的情况,容易造成欠拟合(underfitting),对于特征集过大的情况,容易造成过拟合(overfitting)。针对这两种情况有了更好的解决办法
欠拟合
原因:学习到数据的特征过少
解决办法:增加数据的特征数量
过拟合
原因:原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法:
- 进行特征选择,消除关联性大的特征(很难做)
- 交叉验证(让所有数据都有过训练)
- 正则化
L2正则化
作用:可以使得W的每个元素都很小,都接近于0
优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象