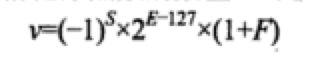在夯实Java基础知识,遇到了浮点数精度问题。总结一下。先看个例子:
public static void main(String[] args) {
double d1 = 0.01;
double d2 = 0.06;
System.out.println(d1 + d2);
}
输出是什么?0.07? 错!
输出结果为: 0.06999999999999999
为什么呢? 这就是本文要讲的内容。
1、float、double不精确问题
计算机世界用二进制表示。有些十进制的数字在二进制世界中是没有办法精切表示的,比如0.2 。
0.01 = 1/4 = 0.25 ,太大
0.001 =1/8 = 0.125 , 又太小
0.0011 = 1/8 + 1/16 = 0.1875 , 逼近0.2了
0.00111 = 1/8 + 1/16 + 1/32 = 0.21875 , 又大了
0.001101 = 1/8+ 1/16 + 1/64 = 0.203125 还是大
0.0011001 = 1/8 + 1/16 + 1/128 = 0.1953125 这结果不错
0.00110011 = 1/8+1/16+1/128+1/256 = 0.19921875
由于浮点数表示的这种“不精确性”或者说是“近似性”, 对于精确度要求不高的运算还行, 如果用float或者double 来做那些要求精确的运算(比如金额计算)时就要小心了, 很可能得不到你想要的结果。
那么浮点数在Java中是如何表示的呢?Java中浮点数分为float跟double. 他们都是使用IEEE754表示的。下面我们简单讲一下IEEE754的基础知识,以及相关的问题。
2、IEEE754 概述
2.1 二进制在计算机中的标识
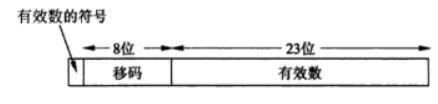
二进制在计算机中可以表示为如下形式:
总结一下有三部分组成:
符号(sign)、有效数M(significant) 、指数E(exponent)
其中基值R是隐含的并且不需要存储,默认为2.
2.2 浮点数的表示
二进制浮点数 组成为:
二进制浮点数 形式为:
通常,阶码所用的表示法为移码表示法。把一个称为偏移量B(bias)的固定值从阶码字段中减去,才得到指数的真值。
关于移码:https://zh.wikipedia.org/wiki/%E7%A7%BB%E7%A0%81
移码主要用于标识浮点数的阶码,在浮点数运算中有优势。
在IEEE754浮点数表示中移码是非标准的,它的偏移值为2^k - 1, 也就是对于单精度浮点数的偏移值为127.
2.3 为什么用移码表示阶码?
浮点数的格式设计首先考虑的是要容易进行整数的比较,特别是用于判断和分类。这也是把符号位置于浮点数格式最左端的缘故。
将阶码字段置于有效数字段的前面,也能通通过整数比较指令简化对浮点数的分类,因为只要两个阶码的符号相同,阶码大的浮点数比阶码小的浮点数看起来要大。
如果采用补码,阶码可能为负,最高位为1,而正数的字段最高位为0,这样由阶码字段看上去,负指数反而像个大数。因此一种解决上述问题的方式就是将阶码字段全部表示为正数。
2.4 为什么选择127作为偏移量B,而不是随意找一个使阶码真值大于0的值,比如200?
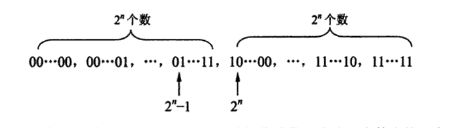
假设阶码字段由n+1 位组成,则总共有2n+1个无符号整数。这2n+1个无符号数对应2 n+1个真指数。显然,选择偏移量B应该使得指数真值的正数和负数分布均匀。2n+1个无符号整数如下:
居于中间的有两个数,2^n -1 和 2^n。可见,选择偏移量B为这两个数中的一个,可以使得指数真值的正数和负数分布基本均匀。
按照上面说法,127跟128都OK,为什么最后定了127呢?
主要是为了让表示的范围能够对称起来
这个算一算就清楚了。
当阶码E 为全0且尾数M 也为全0时,表示的真值x 为零,结合符号位S 为0或1,有正零和负零之分。当阶码E 为全1且尾数M为全0时,表示的真值x 为无穷大,结合符号位S 为0或1,也有+∞和-∞之分。这样在32位浮点数表示中,要除去E,用全0和全1(255)10表示零和无穷大的特殊情况,指数的偏移值不选128(10000000),而127(01111111)。对于规格化浮点数,阶码E范围是1~254。
分两种情况计算如下:
1)偏移值为127时,绝对值范围大致是:1.210^(-38)~3.410^(+38);
2)如果偏移值取为128时, 绝对值范围大致是:5.910^(-39)~1.710^(+38);
可见偏移值取127时,上下范围基本对称,相对合理点。
2.5 IEEE754中浮点数的几个特殊说明
为了是概念清楚,做了如下约定:用大写字母表示IEEE754F浮点数字段中的二进制代码,而相应的小写字母表示对应的真值。如E为阶码,8位长,采用移码表示,阶码E的真值记为e, 于是E = e +B(偏移量)。M为有效数字,M = 1+F ;F为尾数,是有效数的小数部分,23位长,尾数(有效数F的小数部分)的真值记为f。另外用S代表以为符号位,0正1负。
为了表示正无穷和一些特殊的数据,阶码E的最小值为0和最大值255用于特殊用途。因此移码的范围为1254,对应的真值范围为-126127。
IEEE754标准的单精度规格化浮点数数值可以表示为:
3、BigDecimal 的几个关键属性。
/**
* The unscaled value of this BigDecimal, as returned by {@link
* #unscaledValue}.
*
* @serial
* @see #unscaledValue
*/
private final BigInteger intVal;
/**
* The scale of this BigDecimal, as returned by {@link #scale}.
* 数值范围
* @serial
* @see #scale
*/
private final int scale; // Note: this may have any value, so
// calculations must be done in longs
/**
* The number of decimal digits in this BigDecimal, or 0 if the
* number of digits are not known (lookaside information). If
* nonzero, the value is guaranteed correct. Use the precision()
* method to obtain and set the value if it might be 0. This
* field is mutable until set nonzero.
* 精度
* @since 1.5
*/
private transient int precision;
/**
* If the absolute value of the significand of this BigDecimal is
* less than or equal to {@code Long.MAX_VALUE}, the value can be
* compactly stored in this field and used in computations.
* 当BigDecimal 尾数的绝对值小于等于 long的MAX_VALUE, 可以压缩之后放在这个值中。这个值用来计算。
*/
private final transient long intCompact;
在BigDecimal的运算,比如add等操作时,就使用了这几个属性。
在BigDecimal 转double 时,也有可能用到这几个属性。
4、注意不要使用BigDecimal(Double v1)
网上很多人说BigDecimal 可以解决上述问题,先看个例子:
public static void main(String[] args) {
double d1 = 0.01;
double d2 = 0.06;
BigDecimal addend2 = new BigDecimal(d1);
BigDecimal augend2 = new BigDecimal(d2);
BigDecimal result2 = addend2.add(augend2);
System.out.println(result2.doubleValue());
结果仍然是0.06999999999999999, 而不是0.07.
为什么呢?
先说结论,是因为在 new BigDecimal(d1); 过程中,使用了Double.doubleToLongBits(val), 这个过程仍然有不精确的舍入问题。
如果有兴趣,就可以看下源码吧~
public BigDecimal(double val, MathContext mc) {
if (Double.isInfinite(val) || Double.isNaN(val))
throw new NumberFormatException("Infinite or NaN");
// Translate the double into sign, exponent and significand, according
// to the formulae in JLS, Section 20.10.22.
// 注意这儿,将double转成long bits, 会存在舍入的问题!!!
long valBits = Double.doubleToLongBits(val);
// IEEE754: 对于double双精度浮点数,用 1 位表示符号,用 11 位表示指数,52 位表示尾数
int sign = ((valBits >> 63) == 0 ? 1 : -1); // 符号位
int exponent = (int) ((valBits >> 52) & 0x7ffL); // 指数
long significand = (exponent == 0
? (valBits & ((1L << 52) - 1)) << 1
: (valBits & ((1L << 52) - 1)) | (1L << 52)); // 尾数
exponent -= 1075; //指数为什么减去了1075,而不是1023 ????是不是Java Bigdecimal 使用的不是标准IEEE754 ???
// At this point, val == sign * significand * 2**exponent.
/*
* Special case zero to supress nonterminating normalization and bogus
* scale calculation.
*/
if (significand == 0) {
// 尾数为0的情况。
this.intVal = BigInteger.ZERO;
this.scale = 0;
this.intCompact = 0;
this.precision = 1;
return;
}
// Normalize
// 保证了最后一位为偶数。
while ((significand & 1) == 0) { // i.e., significand is even
significand >>= 1;
exponent++;
}
int scale = 0;
// Calculate intVal and scale
BigInteger intVal;
long compactVal = sign * significand;
if (exponent == 0) {
// INFLATED 为 0.
intVal = (compactVal == INFLATED) ? INFLATED_BIGINT : null;
} else {
if (exponent < 0) {
intVal = BigInteger.valueOf(5).pow(-exponent).multiply(compactVal);
scale = -exponent;
} else { // (exponent > 0)
intVal = BigInteger.valueOf(2).pow(exponent).multiply(compactVal);
}
compactVal = compactValFor(intVal);
}
int prec = 0;
int mcp = mc.precision;
if (mcp > 0) { // do rounding
int mode = mc.roundingMode.oldMode;
int drop;
if (compactVal == INFLATED) {
prec = bigDigitLength(intVal);
drop = prec - mcp;
while (drop > 0) {
scale = checkScaleNonZero((long) scale - drop);
intVal = divideAndRoundByTenPow(intVal, drop, mode);
compactVal = compactValFor(intVal);
if (compactVal != INFLATED) {
break;
}
prec = bigDigitLength(intVal);
drop = prec - mcp;
}
}
if (compactVal != INFLATED) {
prec = longDigitLength(compactVal);
drop = prec - mcp;
while (drop > 0) {
scale = checkScaleNonZero((long) scale - drop);
compactVal = divideAndRound(compactVal, LONG_TEN_POWERS_TABLE[drop], mc.roundingMode.oldMode);
prec = longDigitLength(compactVal);
drop = prec - mcp;
}
intVal = null;
}
}
this.intVal = intVal;
this.intCompact = compactVal;
this.scale = scale;
this.precision = prec;
}
5、BigDecimal(String s) 精确
使用BigDecimal(Double d)仍然不精确,那么我们该怎么办呢?
可以使用BigDecimal(String s) 。我们先看个例子:
public static void main(String[] args) {
double d1 = 0.01;
double d2 = 0.06;
BigDecimal addend = new BigDecimal(""+d1);
BigDecimal augend = new BigDecimal(""+d2);
BigDecimal result = addend.add(augend);
System.out.println(result.doubleValue());
}
输出结果终于是0.07. 同样是BigDecimal,为什么Double不行,而string OK了?
是因为在构造BigDecimal(String)时 实际处理的是字符,并没有将double 转换成LongBits.
如果感兴趣,可以看一下源码~
public BigDecimal(char[] in, int offset, int len, MathContext mc) {
// protect against huge length.
if (offset + len > in.length || offset < 0)
throw new NumberFormatException("Bad offset or len arguments for char[] input.");
// This is the primary string to BigDecimal constructor; all
// incoming strings end up here; it uses explicit (inline)
// parsing for speed and generates at most one intermediate
// (temporary) object (a char[] array) for non-compact case.
// Use locals for all fields values until completion
int prec = 0; // record precision value
int scl = 0; // record scale value
long rs = 0; // the compact value in long
BigInteger rb = null; // the inflated value in BigInteger
// use array bounds checking to handle too-long, len == 0,
// bad offset, etc.
try {
// 处理符号位。
boolean isneg = false; // assume positive
if (in[offset] == '-') {
isneg = true; // leading minus means negative
offset++;
len--;
} else if (in[offset] == '+') { // leading + allowed
offset++;
len--;
}
// should now be at numeric part of the significand
boolean dot = false; // true when there is a '.'
long exp = 0; // exponent
char c; // current character
boolean isCompact = (len <= MAX_COMPACT_DIGITS);
// integer significand array & idx is the index to it. The array
// is ONLY used when we can't use a compact representation.
int idx = 0;
if (isCompact) {
// First compact case, we need not to preserve the character
// and we can just compute the value in place.
// 实际处理字符。
for (; len > 0; offset++, len--) {
c = in[offset];
if ((c == '0')) { // have zero
if (prec == 0)
prec = 1;
else if (rs != 0) {
rs *= 10;
++prec;
} // else digit is a redundant leading zero
if (dot)
++scl;
} else if ((c >= '1' && c <= '9')) { // have digit
int digit = c - '0';
if (prec != 1 || rs != 0)
++prec; // prec unchanged if preceded by 0s
rs = rs * 10 + digit;
if (dot)
++scl;
} else if (c == '.') { // have dot
// have dot
if (dot) // two dots
throw new NumberFormatException();
dot = true;
} else if (Character.isDigit(c)) { // slow path
int digit = Character.digit(c, 10);
if (digit == 0) {
if (prec == 0)
prec = 1;
else if (rs != 0) {
rs *= 10;
++prec;
} // else digit is a redundant leading zero
} else {
if (prec != 1 || rs != 0)
++prec; // prec unchanged if preceded by 0s
rs = rs * 10 + digit;
}
if (dot)
++scl;
} else if ((c == 'e') || (c == 'E')) {
exp = parseExp(in, offset, len);
// Next test is required for backwards compatibility
if ((int) exp != exp) // overflow
throw new NumberFormatException();
break; // [saves a test]
} else {
throw new NumberFormatException();
}
}
if (prec == 0) // no digits found
throw new NumberFormatException();
// Adjust scale if exp is not zero.
if (exp != 0) { // had significant exponent
scl = adjustScale(scl, exp);
}
rs = isneg ? -rs : rs;
int mcp = mc.precision;
int drop = prec - mcp; // prec has range [1, MAX_INT], mcp has range [0, MAX_INT];
// therefore, this subtract cannot overflow
if (mcp > 0 && drop > 0) { // do rounding
while (drop > 0) {
scl = checkScaleNonZero((long) scl - drop);
rs = divideAndRound(rs, LONG_TEN_POWERS_TABLE[drop], mc.roundingMode.oldMode);
prec = longDigitLength(rs);
drop = prec - mcp;
}
}
} else {
char coeff[] = new char[len];
for (; len > 0; offset++, len--) {
c = in[offset];
// have digit
if ((c >= '0' && c <= '9') || Character.isDigit(c)) {
// First compact case, we need not to preserve the character
// and we can just compute the value in place.
if (c == '0' || Character.digit(c, 10) == 0) {
if (prec == 0) {
coeff[idx] = c;
prec = 1;
} else if (idx != 0) {
coeff[idx++] = c;
++prec;
} // else c must be a redundant leading zero
} else {
if (prec != 1 || idx != 0)
++prec; // prec unchanged if preceded by 0s
coeff[idx++] = c;
}
if (dot)
++scl;
continue;
}
// have dot
if (c == '.') {
// have dot
if (dot) // two dots
throw new NumberFormatException();
dot = true;
continue;
}
// exponent expected
if ((c != 'e') && (c != 'E'))
throw new NumberFormatException();
exp = parseExp(in, offset, len);
// Next test is required for backwards compatibility
if ((int) exp != exp) // overflow
throw new NumberFormatException();
break; // [saves a test]
}
// here when no characters left
if (prec == 0) // no digits found
throw new NumberFormatException();
// Adjust scale if exp is not zero.
if (exp != 0) { // had significant exponent
scl = adjustScale(scl, exp);
}
// Remove leading zeros from precision (digits count)
rb = new BigInteger(coeff, isneg ? -1 : 1, prec);
rs = compactValFor(rb);
int mcp = mc.precision;
if (mcp > 0 && (prec > mcp)) {
if (rs == INFLATED) {
int drop = prec - mcp;
while (drop > 0) {
scl = checkScaleNonZero((long) scl - drop);
rb = divideAndRoundByTenPow(rb, drop, mc.roundingMode.oldMode);
rs = compactValFor(rb);
if (rs != INFLATED) {
prec = longDigitLength(rs);
break;
}
prec = bigDigitLength(rb);
drop = prec - mcp;
}
}
if (rs != INFLATED) {
int drop = prec - mcp;
while (drop > 0) {
scl = checkScaleNonZero((long) scl - drop);
rs = divideAndRound(rs, LONG_TEN_POWERS_TABLE[drop], mc.roundingMode.oldMode);
prec = longDigitLength(rs);
drop = prec - mcp;
}
rb = null;
}
}
}
} catch (ArrayIndexOutOfBoundsException e) {
throw new NumberFormatException();
} catch (NegativeArraySizeException e) {
throw new NumberFormatException();
}
this.scale = scl;
this.precision = prec;
this.intCompact = rs;
this.intVal = rb;
}
6、总结一套BigDecimal 类库。
/**
* 提供精确的加法运算。
* @param v1 被加数
* @param v2 加数
* @return 两个参数的和
*/
public static double add(double v1,double v2){
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.add(b2).doubleValue();
}
/**
* 提供精确的减法运算。
* @param v1 被减数
* @param v2 减数
* @return 两个参数的差
*/
public static double sub(double v1,double v2){
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.subtract(b2).doubleValue();
}
/**
* 提供精确的乘法运算。
* @param v1 被乘数
* @param v2 乘数
* @return 两个参数的积
*/
public static double mul(double v1,double v2){
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.multiply(b2).doubleValue();
}
/**
* 提供(相对)精确的除法运算。当发生除不尽的情况时,由scale参数指
* 定精度,以后的数字四舍五入。
* @param v1 被除数
* @param v2 除数
* @param scale 表示表示需要精确到小数点以后几位。
* @return 两个参数的商
*/
public static double div(double v1,double v2,int scale){
if(scale<0){
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.divide(b2,scale,BigDecimal.ROUND_HALF_UP).doubleValue();
}
/**
* 提供精确的小数位四舍五入处理。
* @param v 需要四舍五入的数字
* @param scale 小数点后保留几位
* @return 四舍五入后的结果
*/
public static double round(double v,int scale){
if(scale<0){
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b = new BigDecimal(Double.toString(v));
BigDecimal one = new BigDecimal("1");
return b.divide(one,scale,BigDecimal.ROUND_HALF_UP).doubleValue();
}
7、Effective java 48条 给出了另外一种解决方案:
使用int 或者long。
到底选用int或者long取决于所涉及数值的大小,同时要自己处理十进制小数。比如金融领域,可以不以元为单位,而是以分为单位。
8、BigDecimal的坑
1.实例化时使用字符串
2.一定要使用操作后返回值(BigDecimal是不可变的)
3.进行运算前先设置保留几位小数
4.除法运算要在计算时设置保留位数
5.确定要使用哪种进位(四舍五入,还是银行家舍入法)
6.MatchContext不要随便用,根据需要来使用
7.比较两个Decimal是否相等,使用compareTo,不要使用equals
BigDecimal作除法时,除了要考虑除数是否为0,更要考虑是否能除尽的问题,直接调用BigDecimal divide(BigDecimal divisor, int scale, int roundingMode)方法做除法可以避免除不尽的问题。
9、总结
本文先介绍了Java 浮点数为什么存在精度问题,然后又介绍了浮点数表示规则IEEE754,最后介绍了BigDecimal,并引用了《Effective java》的一些结论。其中在IEEE754部分对阶码做了一些常见问题的解答。在BigDecimal 部分强烈推荐使用BigDecimal(String s),而不是BigDecimal(Double d)。
希望对你有用~
最后引用《Effective java》中第48条的描述:
- 对于任何需要精确答案的计算任务,请不要使用float或者double。如果你想让系统来记录十进制小数点,并且不解释因为不使用基本类型而带来的不便,就请使用BigDecimal。
- 如果性能非常关键,并且你又不介意自己记录十进制小数点,而且涉及的数值又不太大,就可以使用int或者long。
- 如果数值没有超过9位十进制数字就用int, 如果不超过18位数字,就可以使用long。 如果数值超了18位,就必须使用BigDecimal.
参考文献
1、浮点数为什么不精确?
2、BigDecimal String的一套类库
后续TODO
(1)分析BigDecimal的源码细节以及BigDecimal 四则运算的实现。
(2)计算机组成原理中与浮点数相关的知识复习,并在Java中实现各种进制之间的转换。