5. Longest Palindromic Substring

题目描述

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

输入与输出

class Solution {
public:
    string longestPalindrome(string s) {
        
    }
};

样例

1. Input："babad"，Output："bab"，Note："aba" is also a valid answer。
2. Input："cbbd"，Output："bb"。

题解与分析

解法一

鉴于 s 的最大长度为1000，可以考虑暴力解法，即枚举每一个可能的中间位置，分别向两侧扩展，得到以该位置为中心的最长回文字串。枚举过程中记录最长回文子串的信息，最后返回子串即可。

该解法中需要注意的一点：回文子串的长度的奇偶性不确定，因此每个位置需要两次扩展过程。

C++ 代码如下：

class Solution {
public:
    string longestPalindrome(string s) {
        int size = s.size();
        int start = -1, length = 0; // 维护最长回文子串相关信息
        // 枚举可能的中心位置
        for (int i = 0; i < size; ++i) {
            // 回文子串长度为奇数的情况
            int left = i - 1, right = i + 1;
            while (left >= 0 && right < size && s[left] == s[right])
                --left, ++right;
            if (right - left - 1 > length)
                start = left + 1, length = right - left - 1;
            // 回文子串长度为偶数的情况
            left = i, right = i + 1;
            while (left >= 0 && right < size && s[left] == s[right])
                --left, ++right;
            if (right - left - 1 > length)
                start = left + 1, length = right - left - 1;
        }
        return s.substr(start, length);
    }
};

该解法的时间复杂度为 O(n^2)。

解法二

与 3. Longest Substring Without Repeating Characters 类似，上述解法的时间复杂度高达 O(n^2) 的原因是没有利用之前枚举过程中得到的信息，导致大量重复的判断。

下面介绍 Manacher 算法，该算法的时间复杂度为 O(n)，缺点是只能处理长度为奇数的回文子串（可以预处理字符串使该算法也适用于偶数长度子串）。

预处理过程：在原字符串两端与字符之间插入原字符串中未出现过的字符（本文中使用 '#'），例如 abacabba 处理后为 #a#b#a#c#a#b#b#a#。这样所有的回文子串均为奇数长度，例如 #a#b#a#、#a#b#b#a#。

设处理过的字符串为 Ma，建立一个同等长度的 int 数组 Mp。Mp[i]用来记录以位置i为中心的最长回文子串的右半部分的长度（不包括位置i本身），例如#a#b#b#a#的右半部分为b#a#，相应地，Mp[i] = 4。通过上例还可以得到Mp数组的另一个意义，它记录了相应回文子串在原字符串对应的长度。

除此之外，建立变量Mx用来记录当前所有扩展过程中涉及到的最右侧字符的位置，建立变量Id记录扩展到该位置时的中心位置。

下面分情况讨论该算法如何利用之前枚举过程中的信息，也是该算法的核心，对应代码Mp[i] = Mx > i ? min(Mp[2 * Id - i], Mx - i) : 0;。

• 首先判断Mx与i的位置关系：
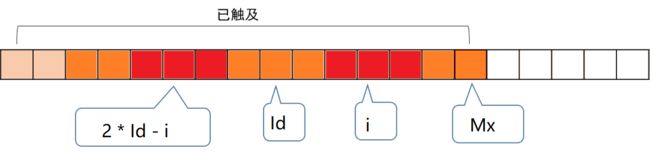
• Mx > i：说明之前某个回文子串曾经扩展到该位置右侧，则该位置两侧字符中有一部分信息之前获取过。这部分信息保存在Mp[2 * id - i]中，其中2 * id - i是i关于Id的对称位置。进一步讨论：
• Mp[2 * Id - i] <= Mx - i：即以2 * id - i为中心的最长回文子串在以id为中心的最长回文子串内部，如下图所示：
  
  
  
  由于橙色部分是回文子串，那么两个红色部分是镜像关系，如果左侧红色部分是最长回文子串，那么右侧红色部分也是对应位置的最长回文子串。即Mp[i] = Mp[2 * Id - i]。
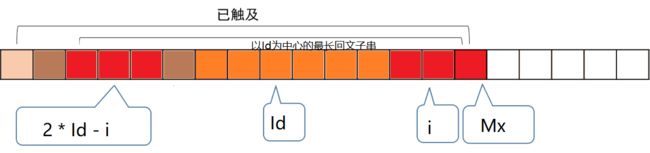
• Mp[2 * Id - i] > Mx - i：即以2 * id - i为中心的最长回文子串的左侧超出了以id为中心的最长回文子串。如下图所示：
  
  
  
  与上种情况类似，但是以2 * id - i为中心的最长回文子串中只有红色部分在以id为中心的最长回文子串内部，因此右侧对应的红色部分也是回文子串。但是在Mx右侧的字符尚未拓展，因此需要进一步拓展获得最大回文子串。初始化Mp[i] = Mx - i。
• Mx <= i：这种情况下i右侧的字符尚未拓展过，需要拓展获得最长回文子串。初始化Mp[i] = 0。

C++ 代码如下：

class Solution {
public:
    string longestPalindrome(string s) {
        int size = s.size() * 2 + 1;
        char *Ma = new char[size];
        int *Mp = new int[size];
        int Mx = -1, Id = -1;
        int start, length = 0;
        Ma[0] = '#';
        for (int i = 0, p = 0; i < s.size(); ++i) {
            Ma[++p] = s[i];
            Ma[++p] = '#';
        }
        for (int i = 0; i < size; ++i) {
            Mp[i] = Mx > i ? min(Mp[2 * Id - i], Mx - i) : 0;
            while (i - Mp[i] - 1 >= 0 && i + Mp[i] + 1 < size && Ma[i - Mp[i] - 1] == Ma[i + Mp[i] + 1])
                ++Mp[i];
            if (i + Mp[i] > Mx)
                Mx = i + Mp[i], Id = i;
            if (Mp[i] > length)
                length = Mp[i], start = (i - Mp[i]) / 2;
        }
        delete[] Ma;
        delete[] Mp;
        return s.substr(start, length);
    }
};

时间复杂度分析：上述代码中，第一个 for 循环为 O(n)，第二个 for 循环外层为 O(n)，下面分析内部的 while 循环。由上述算法流程可知，每一次扩展操作都是在Mx右侧扩展，即每执行一次++Mp[i];都会导致Mx增加 1，即Mx单调递增。因为Mx的取值范围是[0, size)，所以 while 循环内部代码最多执行 O(n) 次。

该解法的时间复杂度为 O(n)。