前置知识点概要:离散Hopfield神经网络+模拟退火+隐单元=Boltzman机
1、玻尔兹曼机BM
分隐藏层h、可见层v(即输入层,也是输出层)。玻尔兹曼机可以看作全连通图,即每个神经元和本层所有神经元、其他层神经元全链接
2、受限玻尔兹曼机RBM
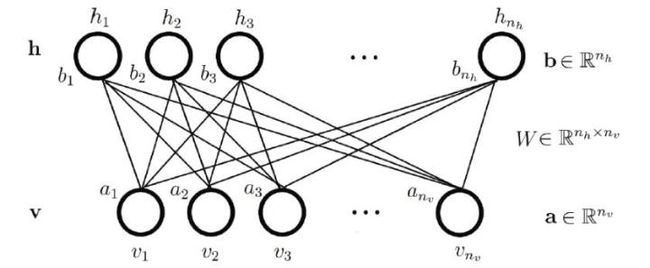
层内不连接,与其他层所有神经元链接,其中vi是可见层神经元,hj是隐藏层神经元,ai可见层偏置,bj隐藏层偏置,W权重矩阵
2.1 概念理解 转自 https://blog.csdn.net/u013631121/article/details/76652647
对单个样本v,可通过加权求和加上偏置(对所有i∑viWij+bj),求得h,然后再用同样方法反向传播计算,得到v',对所有的vi和v‘i做差加和,可以得到一个值。我们希望的是这个值越小越好。
也就是如果把v->h,h->v'视为一个编码和解码的过程的话,我们希望解码出来的东西能和原来的一致。如果用统计的角度,可以把P(v)看作解码后是v的概率(也就是解码的准确率),也就是P(v)越大越好,即求最大值。(能量函数相关知识待学习,此为猜测)
2.2 训练 转自 https://blog.csdn.net/xbinworld/article/details/45013825 以及 https://www.cnblogs.com/pinard/p/6530523.html
2.2.1 前置知识点 转自 https://blog.csdn.net/xbinworld/article/details/43612641
MCMC、吉布斯采样:
简述:对于复杂分布,很难直接采样。利用数学工具马尔科夫链的稳态形式服从某种分布,去构造服从特殊分布的马尔科夫链,再从中采样,就可得到复杂采样的样本
2.2.2 能量函数、概率分布计算
公式详见转载博客,此处不再赘述,只记录个人理解
定义能量函数E(v,h)
得到基于能量函数的概率分布P(v,h),此处做疑问,概率论知识待学习
可求得P(v),P(h),P(h|v),P(v|h),P(hj=1|v),P(vi=1|h)
需要能量函数E为最小时网络稳定,利用梯度下降思路,做损失函数L=ln(P(v)),再求L对vi、hj、wij的梯度然后进行梯度下降迭代。为什么是P(v)而不是E呢?个人理解是,对P的表达式,E的绝对值越大,P越大,也就是有相同的增减性,而P的形式便于梯度求导。
梯度表达式中复杂分布不容易求解,但是表现为期望形式,则使用吉布斯采样或者MC算法采样,均值即为期望的无偏估计
2.3 应用
一般不做单独使用,而是作为特征提取器或者预训练手段,列几个用途,并作为以后学习点
DBM:深玻尔兹曼机,每一层都是RBM,前一层的h作为下一层的v,逐层训练
DBN:深度信念网络,每层都是RBM。先做逐层训练,然后用bp训练