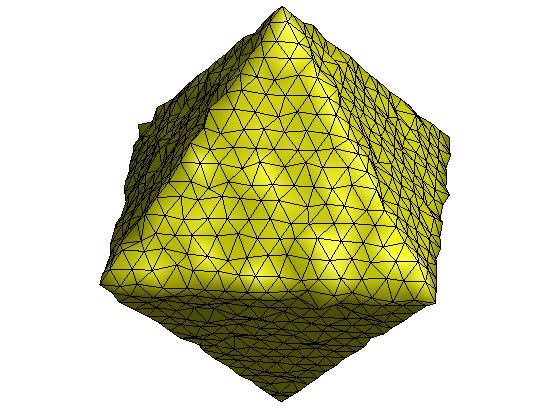
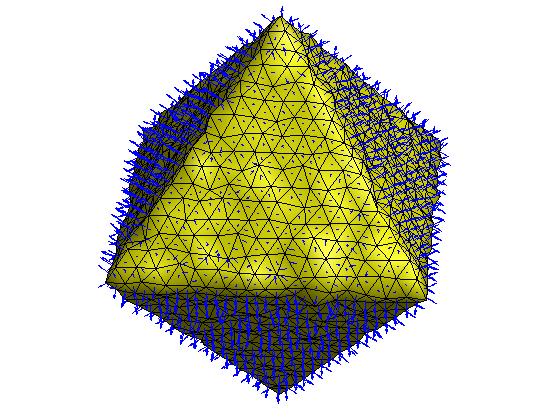
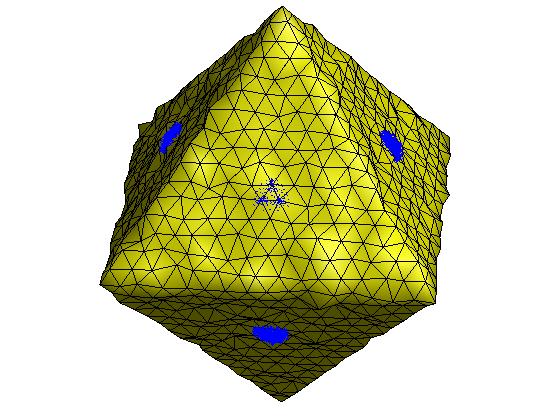
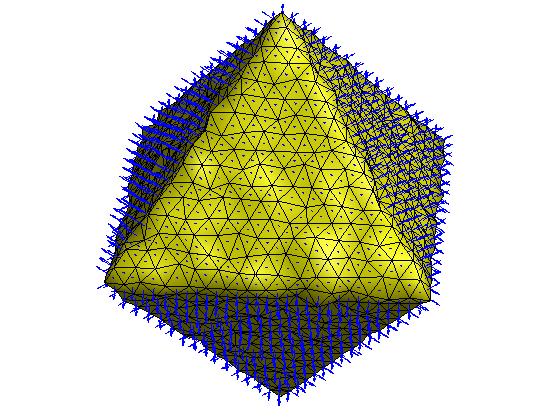
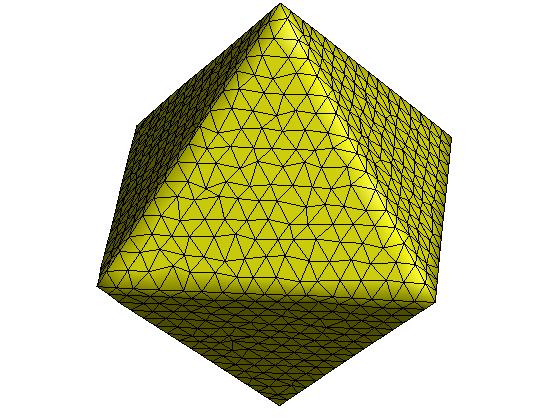
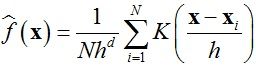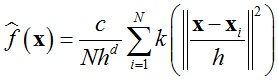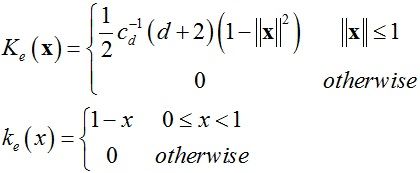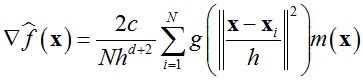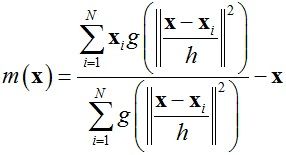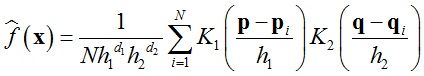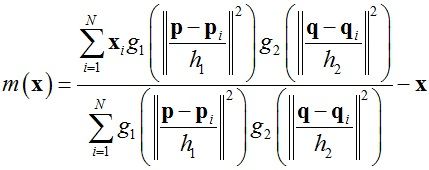mean shift算法是一种强大的无参数离散数据点的聚类方法,其在图像平滑、图像分割以及目标跟踪等方面都有着广泛的应用。[Yamauchi et al. 2005]基于mean shift算法提出了一种网格分割方法,具体来说,给定一个三角网格,其面片重心和面片法向可以组成6维特征空间中的一系列离散点集,然后使用mean shift算法对其进行聚类,聚类后每个面片的法向可以修正为各自聚类中心的法向信息,最后基于面片修正法向进行网格分割。下面具体介绍该算法的过程。
给定一个由面片{Ti}所组成的三角网格M,其面片重心{ci}和面片法向{ni}组成R6空间中的离散点集χ = {(pi, qi) = (ci, ni)}。利用mean shift算法对其进行聚类之后,对每个聚类中心yi[c] = {(p, q)的法向部分归一化之后可以作为该类中三角面片的新法向。
修正后的面片法向有两个应用,一个是网格光顺,另一个是网格分割。对于网格分割应用,需要指定网格分割的区域数目。在初始化阶段,先随机选定各个区域的种子面片,然后迭代以下两个步骤直到收敛稳定。
1:区域增长
相邻三角面片Ti和Tj之间的距离定义为:
distance(Ti, Tj) = || Nmi – Nmj ||
其中Nm为利用mean shift算法得到的面片修正法向。
这样利用多源Dijkstra最短路算法可以为每个三角面片指定一个所属区域。
2:计算种子面片
区域增长完成后,需要重新计算每个区域的种子面片,新的种子面片为每个区域最中心的三角面片。因此该阶段相邻三角面片Ti和Tj之间的距离定义为:
distance(Ti, Tj) = || ci – cj ||
其中ci为三角面片Ti的重心。
这样每个区域可以找到一个距离边界最远的三角面片,即为新的种子面片。
图:(上左)原始网格 (上中)原始网格法向 (上右)mean shift聚类
(下左)网格修正法向 (下中)网格分割效果 (下右)网格光顺效果
参考文献:
[1] Hitoshi Yamauchi, Seungyong Lee, Yunjin Lee, Yutaka Ohtake, Alexander Belyaev, and Hans-Peter Seidel. 2005. Feature Sensitive Mesh Segmentation with Mean Shift. In Proceedings of the International Conference on Shape Modeling and Applications 2005 (SMI '05). IEEE Computer Society, Washington, DC, USA, 238--245.
附录
Mean-shift算法
利用某个概率密度函数f(x)采样得到一系列数据样本χ = (x1, x2, … , xn)∈Rd。假设我们需要估计这些样本的概率密度函数f(·),那么由核密度估计(kernel density estimation)方法可以近似得到其概率密度函数为:
其中K(x)称为核函数(kernel function),h为带宽(bandwidth)。核函数满足如下条件:
一般核函数是满足径向对称(radially symmetric),即可以表示为:
其中k(x)称为分布函数(profile function),c为归一化参数。
于是概率密度函数可以转化成如下形式:
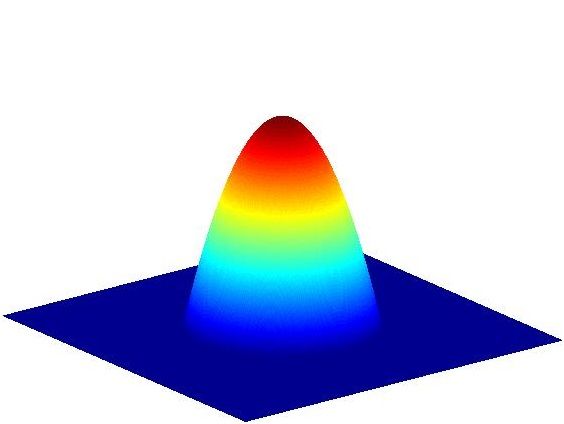
一般使用较多的核函数是Gaussian核函数和Epanechnikov核函数,其具体形式如下:
Gaussian核函数:
Epanechnikov核函数:
其中cd是d维单位球的体积。
假设将数据样本χ聚类成一系列簇,我们可以将聚类中心设定为概率密度函数的局部极值点,而寻找局部极值点的一个最简单方法就是梯度上升法。
对概率密度函数求导后得到:
其中g(x) = -k’(x),m(x)的形式如下:
上式中的m(x)就是所谓的mean shift向量,它的物理含义就是概率密度函数的梯度,也就是当前点的移动方向和大小。
利用mean shift算法进行聚类的过程分如下两步:
1. 对于每一个数据样本xi∈χ,初始化xi为yi[0];
2. 利用梯度上升方法计算yi[j]直到收敛,yi[j+1] = yi[j] + m(yi[j]),j = 0, 1, 2, …。
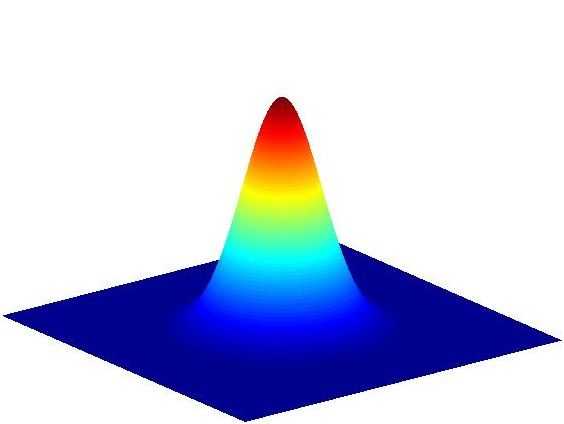
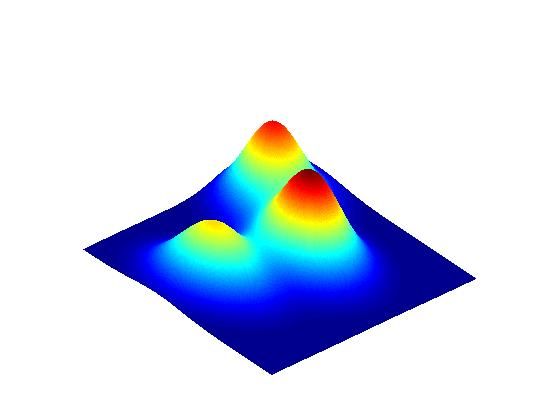
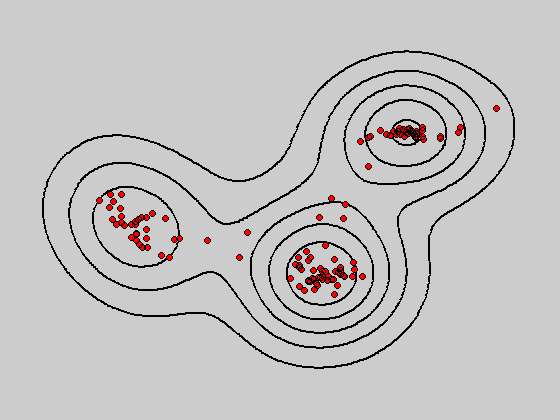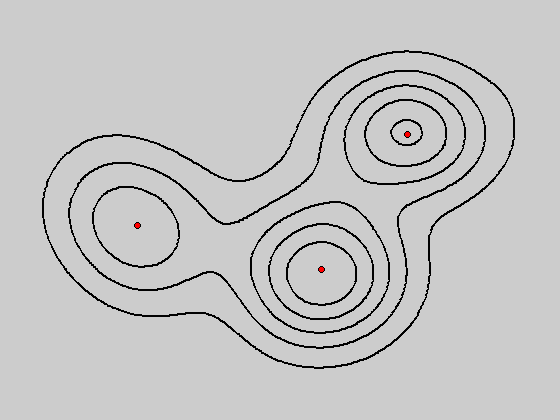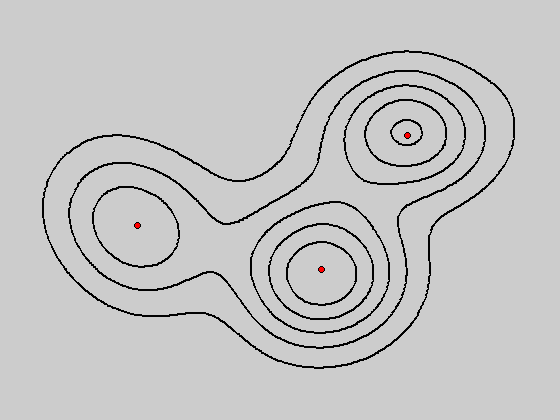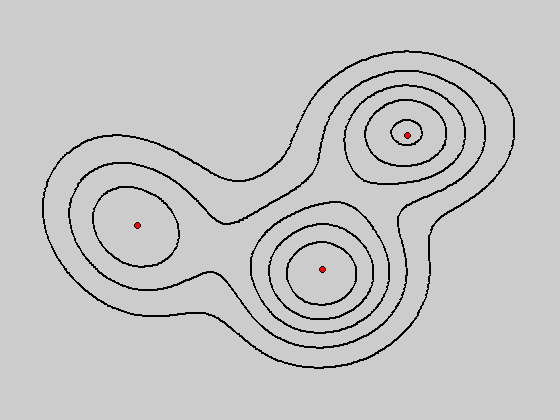
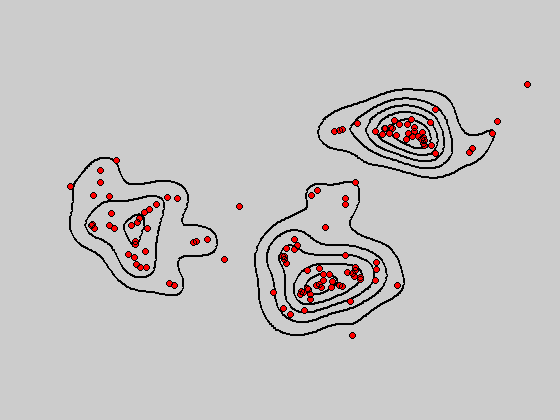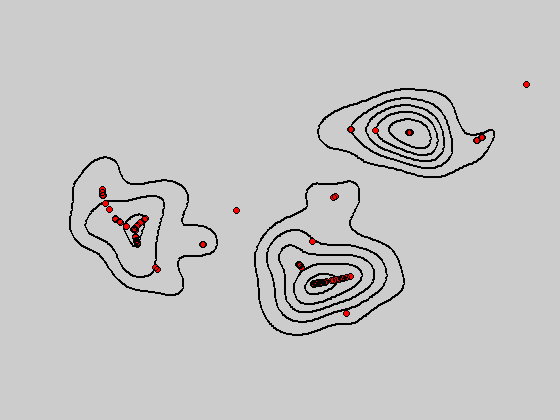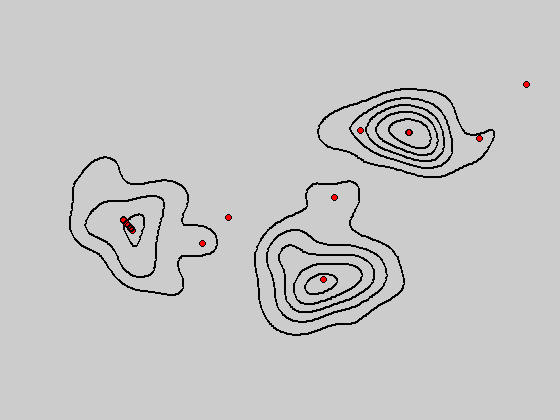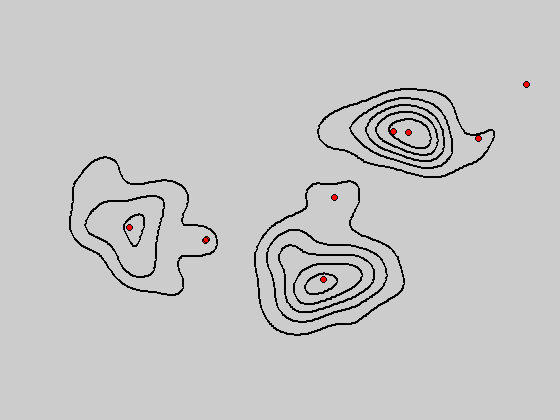
对于如下二维数据样本,利用核密度估计方法可以得到不同带宽下的概率密度函数分布,并且利用mean shift算法可以得到不同的聚类结果。
图:原始二维数据样本
图:bandwidth = 2和bandwidth = 0.8所对应的概率密度函数分布图
图:bandwidth = 2和bandwidth = 0.8所对应的mean shift聚类效果
上述mean shift算法有个简单的扩展,对于数据样本χ = {xi= (pi, qi): pi∈P, qi∈Q},每个样本由两部分内容组成,那么使用多元核密度估计(multivariate kernel density estimation)方法可以得到其概率密度函数为:
此时mean shift向量为:
本文为原创,转载请注明出处:http://www.cnblogs.com/shushen。
参考:
http://blog.csdn.net/ttransposition/article/details/38514127