- WHAM 人体3d重建部署笔记
AI算法网奇
深度学习宝典3d笔记
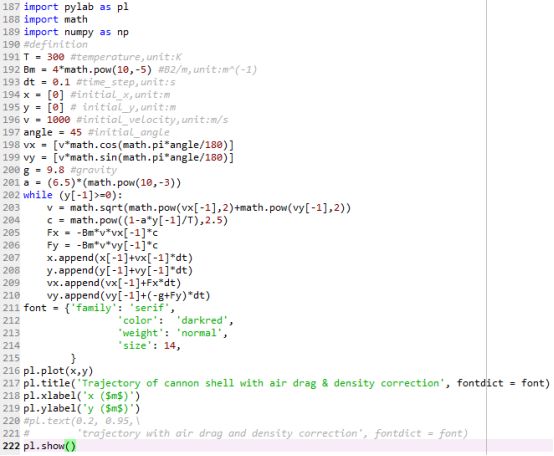
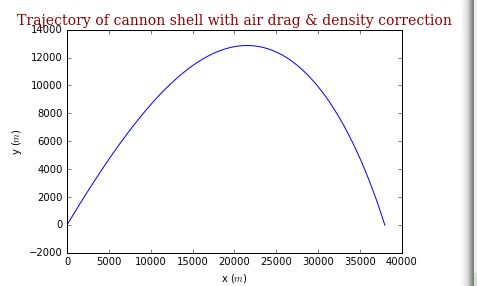
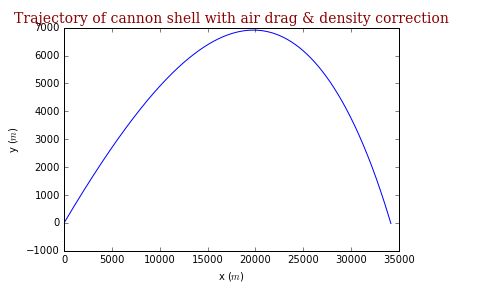
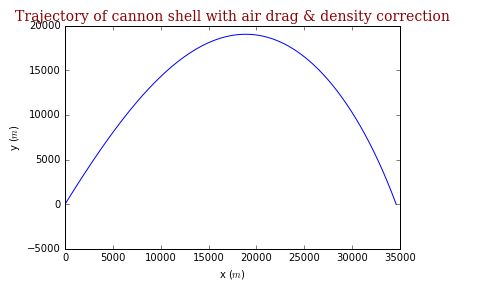
目录依赖项:mmpose的依赖项:demo脚本WHAM:ReconstructingWorld-groundedHumanswithAccurate3DMotion2024依赖项:pipinstallmmposemmpose的依赖项:mmcv>=2.0.0,=3.0.0,=0.4.0,<1.0.0demo脚本Youcantrywithoneexamplarvideo:pythondemo.py--
- 探索Sfm-python: 一款强大的计算机视觉库
缪昱锨Hunter
探索Sfm-python:一款强大的计算机视觉库去发现同类优质开源项目:https://gitcode.com/在计算机视觉领域,Sfm-python是一个值得关注的开源项目,它以简洁高效的Python接口提供结构化从运动(StructurefromMotion,SfM)算法。如果你对3D重建、图像匹配或地理定位有兴趣,那么这个项目将是你不可或缺的工具。让我们一起深入了解一下它的技术细节、应用场景
- 【ai】mocap:conda 安装python3.8+ cuda+ pytorch+torchaudio、torchvision
等风来不如迎风去
AI入门与实战人工智能ubuntuconda
MotionCapubuntu18.04不知道为啥会依赖于ffmpeg、xorg渲染?安装pytorch就是会带上cudacudnn啥的pytorch【ai】tx2nx:安装torch、torchvisionforyolov5这里就发现pytorch和torchvision有依赖关系的,还涉及到rapidjson所以python的环境隔离很重要。核心库-cudatoolkit=11.3-pytor
- 游戏成瘾与学习动力激发策略研究——了解“情感解离”“创伤理论”
*TQK*
知也思维认知心理学研究
一、情感解离(EmotionalDissociation)定义:情感解离是一种心理防御机制,指个体在经历无法承受的情绪压力或创伤时,通过切断情感体验与认知、记忆或现实感知的联系来保护自我。它不是简单的“麻木”,而是大脑为应对极端刺激而启动的“紧急逃生通道”。核心特征1、意识分裂现实解离:感到身体或环境“不真实”(如玩游戏时出现“灵魂出窍”般的视角抽离)情感隔离:能描述事件但无法体验对应情绪(如你通
- Embrace Collisions: Humanoid Shadowing for Deployable Contact-Agnostics Motions
酒吧舞男
论文阅读
EmbraceCollisions:HumanoidShadowingforDeployableContact-AgnosticsMotions研究动机解决方案技术路线方法限制实验结果EmbraceCollisions:HumanoidShadowingforDeployableContact-AgnosticsMotions研究动机运动命令接口挑战:当机器人经历显著滚转或俯仰旋转时,运动命令难以
- android camera慢动作,关于android:这可能是全网关于Camera慢动作录像SlowMotion介绍最全的文章了...
weixin_42465953
androidcamera慢动作
这是一篇对于慢动作录像(slowmotion)的文章,看完后置信你对慢动作录像不会再感到生疏了~这篇文章针对上面几点来开展:1)写这篇文章的原由?2)什么是慢动作录像(SlowMotionRecord)?3)Android上如何实现慢动作录像?4)调试demo下载地址?5)调试遇到的问题及解决?一、写这篇文章的原由?2月份的时候,在一个音视频开发的学习交换群里,有位网友问到“Android相机有啥
- 第29讲 Android Camera2 API SlowMotion实战
deepinout_camera
AndroidCamera2API详解androidhtml5
本讲是AndroidCamera专题系列的第29讲,我们介绍AndroidCamera2API专题的SlowMotion实战,包括如下内容:判断是否支持SlowMotionSlowMotion支持的Size和FPSCamera流程控制MediaRecorder流程控制视频在线观看:极客笔记:极客笔记在线课程判断是否支持SlowMotionCamera方面Capability是否支持REQUEST_
- Stable Diffusion游戏底模推荐
Liudef06
从零开始设计游戏stablediffusion游戏
一、基础通用型底模SDXLbase官方原版底模,支持1024x1024高清出图,适用于各类游戏场景和角色的基础生成,建议作为微调训练的基准模型。来源:相关搜索结果写实风格搭配推荐搭配9realisticSDXL或麻袋realistic_XL,增强光影真实感和皮肤细节表现。来源:相关搜索结果二、二次元/动漫风格animagineXLV3_v30专为二次元优化的底模,适合日系动漫角色设计,支持高精度面
- 情感识别(Emotion Recognition)
路野yue
人工智能自然语言处理
情感识别(EmotionRecognition)是通过分析人类的多模态数据(如面部表情、语音、文本等)来识别和理解其情感状态的技术。它在人机交互、心理健康、市场分析等领域有广泛应用。情感识别的主要方法1.基于面部表情的情感识别方法:通过分析面部特征(如眼睛、嘴巴、眉毛等)来识别情感。技术:传统方法:使用特征提取(如Gabor滤波器、LBP)和分类器(如SVM)。深度学习方法:使用卷积神经网络(CN
- 多模态模型在做选择题时,如何设置Prompt,如何精准定位我们需要的选项
暗巷提灯
prompt
我们这里以Qwen2-VL-7B-instruct为例:假设我们需要分析一张图片的情绪(从现有的情绪中进行选择),并且我们需要它以思维链的形式展现出来,我们可以这样设置prompt:emotion6_CoT="""Analyzethegivenimageanddeterminetheemotionitrepresents.Emotionaloptions:(A)anger(B)disgust(C)
- 基于Pytorch的语音情感识别系统
鱼弦
人工智能时代pytorch人工智能python
基于Pytorch的语音情感识别系统介绍语音情感识别(SpeechEmotionRecognition,SER)是指通过分析和处理人的语音信号来识别其情感状态。常见的情感状态包括愤怒、喜悦、悲伤、惊讶等。基于Pytorch的语音情感识别系统使用深度学习技术,通过训练神经网络模型来实现情感识别任务。应用使用场景客户服务中心:自动识别客户情绪,提供有针对性的服务。智能语音助手:提升人机交互体验,更加智
- Rocky DEM tutorial5_Drop Weight test_落锤试验
Sim Pro (理想)
一起来学RockyDEMRockyDEM
tutorial5_DropWeighttest_落锤实验文章目录tutorial5_DropWeighttest_落锤实验0.目的1.模型介绍2.模型设置2.1设置Physics2.2导入几何2.3定义进口面2.4设置motionframes2.5设置边界条件2.6设置材料2.7设置materialsinteractions2.8设置Particles2.9设置破碎模型2.10设置进口2.11求
- c#视觉应用开发中如何在C#中处理多光谱图像?
openwin_top
C#视觉应用开发问题系列c#开发语言计算机视觉视觉检测
microPythonPython最小内核源码解析NI-motion运动控制c语言示例代码解析python编程示例系列python编程示例系列二python的Web神器Streamlit如何应聘高薪职位在C#中处理多光谱图像(MultispectralImaging,MSI)通常涉及多个步骤,包括图像读取、处理和显示。多光谱图像包含多个频带(通常超过人类视觉的RGB频带),需要特殊处理才能进行分析
- C#开发串口通讯软件如何如何避免串口通讯中的资源竞争?
openwin_top
c#串口应用开发问题系列c#开发语言串口上位机通讯
microPythonPython最小内核源码解析NI-motion运动控制c语言示例代码解析python编程示例系列python编程示例系列二python的Web神器Streamlit如何应聘高薪职位在C#中开发串口通讯软件时,避免资源竞争是确保系统稳定性和数据完整性的关键。资源竞争通常发生在多个线程或进程同时访问同一个串口资源时。为了避免这种情况,可以采取以下措施:使用锁机制(Lock):使用
- 探索路径规划的艺术:CurvesGenerator - 优雅的曲线生成器
邹澜鹤Gardener
探索路径规划的艺术:CurvesGenerator-优雅的曲线生成器CurvesGeneratorCommonusedcurvesformotionplanning.项目地址:https://gitcode.com/gh_mirrors/cu/CurvesGenerator项目介绍在机器学习、自动驾驶和游戏开发等领域中,精确且平滑的路径规划是至关重要的。CurvesGenerator是一个开源项目
- VMware各个软件的作用
The god of big data
大Big数据Data教程神器?三叉戟?云计算网络
VMware作为全球领先的虚拟化与云计算解决方案提供商,其软件产品覆盖了从桌面级虚拟化到企业级云平台的全场景需求。以下结合其核心产品体系,详细解析各软件的功能定位与业务价值:一、基础虚拟化平台VMwarevSphere作为企业级服务器虚拟化的核心引擎,vSphere通过ESXi虚拟化内核实现对物理服务器的资源切割,支持在一台物理主机上同时运行数百个虚拟机(VM)。其核心功能包括:vMotion:实
- 自动驾驶---Motion Planning之轨迹Path优化
智能汽车人
自动驾驶人工智能
1背景在之前的几篇文章中,不管是通过构建SL图《自动驾驶---MotionPlanning之PathBoundary》,ST图《自动驾驶---MotionPlanning之SpeedBoundary》,又或者是构建SLT图《自动驾驶---MotionPlanning之构建SLTDrivingCorridor》,最终我们都是为了得到boundary的信息。构造优化问题求解的前提:首先确定问题的代价函
- 多体动力学仿真软件:SolidWorks Motion_(9).仿真参数设置
kkchenjj
多体动力学仿真模拟仿真仿真模拟多体动力学
仿真参数设置在多体动力学仿真软件中,仿真参数的设置是确保仿真结果准确性和可靠性的关键步骤。合理的参数设置不仅能够提高仿真的效率,还能确保仿真过程中的物理行为符合实际。本节将详细介绍如何在SolidWorksMotion中设置仿真参数,包括时间步长、求解器选择、收敛标准、接触和摩擦参数等。时间步长时间步长是仿真过程中每个时间点的间隔。选择合适的时间步长对于仿真过程的稳定性和准确性至关重要。时间步长过
- esp-who配置与编译流程分析 - esp32-s3-eye
生活需要深度
esp32-eye配置编译
book@100ask:~/esp/esp-who/examples/motion_detection/lcd$idf.pyset-targetesp32s3Adding"set-target"'sdependency"fullclean"tolistofcommandswithdefaultsetofoptions.Executingaction:fullcleanBuilddirectory'
- 多体动力学仿真软件:SolidWorks Motion_(3).多体动力学基本概念
kkchenjj
多体动力学仿真模拟仿真仿真模拟多体动力学
多体动力学基本概念多体系统定义多体系统是由多个刚体和/或柔体通过各种连接和约束组成的机械系统。每个体可以是独立的刚体,也可以是具有内部自由度的柔体。多体系统中的体之间通过关节、弹簧、阻尼器等连接元件相互作用,形成一个复杂的运动和力的传递网络。在多体动力学仿真中,我们需要考虑这些体之间的相对运动、相互作用力以及系统整体的运动学和动力学特性。1.刚体和柔体刚体:在多体动力学中,刚体是指在受力作用下不发
- 三维重建(十三)——多视角重建
周末不下雨
三维重建三维重建3d
文章目录一、多视角重建1.1SFM(StructurefromMotion)1.2NRSFM(Non-RigidStructurefromMotion)1.3TheRelightables:VolumetricPerformanceCaptureofHumanswithRealisticRelighting二、基于可微渲染的多视角重建三、数据采集策略3.1相机配置与布置3.2视角覆盖与重叠3.3光
- 自动驾驶---如何打造一款属于自己的自动驾驶系统
智能汽车人
自动驾驶技术自动驾驶人工智能
在笔者的专栏《自动驾驶Planning决策规划》中,主要讲解了行车的相关知识,从Routing,到BehaviorPlanning,再到MotionPlanning,以及最后的Control,笔者都做了相关介绍,其中主要包括算法在量产上的应用,这是笔者与其他博主非常不同的一点,重点阐述自动驾驶量产相关的算法。在之前的专栏中由于篇幅的限制,并不能逐篇去扣算法,扣代码。只是希望读者朋友们对整个自动驾驶
- 人工智能训练师如何做图像数据标注,从情感分析和实体分析两个个场景分析
小宝哥Code
人工智能训练师人工智能
在人工智能训练中,图像情感分析和图像实体分析是两个重要的应用场景。高质量的图像数据标注对于训练情感识别模型和目标检测/语义分割模型至关重要。本指南将详细介绍:情感分析标注(EmotionAnalysis)实体分析标注(EntityRecognition)自动化标注工具Python代码示例数据格式与存储标注数据质量评估1.情感分析(EmotionAnalysis)标注1.1情感分析简介图像情感分析(
- 基于Python的情感分析与情绪识别技术-从基础到前沿应用
一键难忘
python开发语言情感分析
基于Python的情感分析与情绪识别技术-从基础到前沿应用一、情感分析与情绪识别基础概念1.1核心概念区分情感分析(SentimentAnalysis)与情绪识别(EmotionRecognition)是自然语言处理领域的重要分支,二者存在本质差异:情感分析侧重判断文本的极性(正面/负面/中性)情绪识别需识别具体情绪类别(喜悦、愤怒、悲伤等)传统情感分析多采用二值分类,而情绪识别属于多标签分类问题
- android滑动看新闻
太空漫步11
android
packagecom.example.myapplication5;importandroidx.appcompat.app.AppCompatActivity;importandroid.os.Bundle;importandroid.view.GestureDetector;importandroid.view.MotionEvent;importandroid.view.View;impor
- Android 模拟手柄摇杆输入,模拟MotionEvent
BrainZou
Androidandroid手柄摇杆MotionEvent
背景需求是在系统应用模拟摇杆,达到对所有应用都能模拟输入的效果,所以一定会使用到InputManager。但是大多demo和文章模拟摇杆和功能使用都是在同一个应用,所以可以自定义实现此类功能,不需要模拟构造MotionEvent给InputManager相关代码和使用建议先查看Google的对手柄处理文档,对手柄有一定的了解:https://developer.android.com/traini
- 【论文精读】MotionLM
EEPI
自动驾驶深度学习论文阅读
【论文精读】MotionLM1背景2存在的问题3具体方案轨迹转运动序列模型轨迹去重和聚类loss1背景团队:Waymo时间:2023.9代码:简介:采用自回归的方式做轨迹生成,能够更好地建模交互,且避免模态坍缩,在数据集达到了SOTA。2存在的问题轨迹回归方面:原本xy预测认为空间过大,有的xy很大(t大速度快的时候),有的xy很小(t小速度慢的时候)。3具体方案Encoder采用了之前的论文Wa
- Android App开发之Jetpack架构,带你全面理解View的绘制流程
m0_66144992
程序员架构移动开发android
在UI组件日益完善的同时,也开始出现了RecyclerView、ConstraintLayout、MotionLayout等一些可以辅助大家写出更加符合性能要求的界面效果。在UI控件日益满足需求的同时,系统的安全与稳定性、用户隐私也越来越被重视,所以每个版本都出现了一些大的适配工作,例如运行时权限,FileProvider适配,限制后台服务、广播,限制反射SDK私有API,引导使用HTTPS,甚至
- 自动驾驶---Motion Planning之参考线Path平滑
智能汽车人
自动驾驶人工智能
1背景有了由lane_segment插值得到的粗糙参考线,这种参考线是无法输出给下游使用的,需要进一步的处理使得参考线更加平滑,才能供下游控制模块使用。Apollo中共有三种参考线平滑算法,分别为:1.QpSplineSmoother2.SpiralReferenceLineSmoother3.DiscretePointsSmoother目前Apollo中默认配置为最后一种,基于离散点的平滑。这种
- 自动驾驶---Motion Planning之LaneChange
智能汽车人
自动驾驶人工智能
1背景在Apollo中,有比较多的Decider(决策器),上篇博客《自动驾驶---MotionPlanning之Decider》中笔者也大概介绍了每个Deicder的作用。本篇博客笔者主要介绍换道的决策内容,因为在自动驾驶中(严格意义上来讲,目前还属于辅助驾驶),变道的灵活性是用户评价该功能是否好用很重要的一部分,变道迟缓或者激进都是不好的体验,所以本篇博客会结合Apollo中的LaneChan
- SAX解析xml文件
小猪猪08
xml
1.创建SAXParserFactory实例
2.通过SAXParserFactory对象获取SAXParser实例
3.创建一个类SAXParserHander继续DefaultHandler,并且实例化这个类
4.SAXParser实例的parse来获取文件
public static void main(String[] args) {
//
- 为什么mysql里的ibdata1文件不断的增长?
brotherlamp
linuxlinux运维linux资料linux视频linux运维自学
我们在 Percona 支持栏目经常收到关于 MySQL 的 ibdata1 文件的这个问题。
当监控服务器发送一个关于 MySQL 服务器存储的报警时,恐慌就开始了 —— 就是说磁盘快要满了。
一番调查后你意识到大多数地盘空间被 InnoDB 的共享表空间 ibdata1 使用。而你已经启用了 innodbfileper_table,所以问题是:
ibdata1存了什么?
当你启用了 i
- Quartz-quartz.properties配置
eksliang
quartz
其实Quartz JAR文件的org.quartz包下就包含了一个quartz.properties属性配置文件并提供了默认设置。如果需要调整默认配置,可以在类路径下建立一个新的quartz.properties,它将自动被Quartz加载并覆盖默认的设置。
下面是这些默认值的解释
#-----集群的配置
org.quartz.scheduler.instanceName =
- informatica session的使用
18289753290
workflowsessionlogInformatica
如果希望workflow存储最近20次的log,在session里的Config Object设置,log options做配置,save session log :sessions run ;savesessio log for these runs:20
session下面的source 里面有个tracing
- Scrapy抓取网页时出现CRC check failed 0x471e6e9a != 0x7c07b839L的错误
酷的飞上天空
scrapy
Scrapy版本0.14.4
出现问题现象:
ERROR: Error downloading <GET http://xxxxx CRC check failed
解决方法
1.设置网络请求时的header中的属性'Accept-Encoding': '*;q=0'
明确表示不支持任何形式的压缩格式,避免程序的解压
- java Swing小集锦
永夜-极光
java swing
1.关闭窗体弹出确认对话框
1.1 this.setDefaultCloseOperation (JFrame.DO_NOTHING_ON_CLOSE);
1.2
this.addWindowListener (
new WindowAdapter () {
public void windo
- 强制删除.svn文件夹
随便小屋
java
在windows上,从别处复制的项目中可能带有.svn文件夹,手动删除太麻烦,并且每个文件夹下都有。所以写了个程序进行删除。因为.svn文件夹在windows上是只读的,所以用File中的delete()和deleteOnExist()方法都不能将其删除,所以只能采用windows命令方式进行删除
- GET和POST有什么区别?及为什么网上的多数答案都是错的。
aijuans
get post
如果有人问你,GET和POST,有什么区别?你会如何回答? 我的经历
前几天有人问我这个问题。我说GET是用于获取数据的,POST,一般用于将数据发给服务器之用。
这个答案好像并不是他想要的。于是他继续追问有没有别的区别?我说这就是个名字而已,如果服务器支持,他完全可以把G
- 谈谈新浪微博背后的那些算法
aoyouzi
谈谈新浪微博背后的那些算法
本文对微博中常见的问题的对应算法进行了简单的介绍,在实际应用中的算法比介绍的要复杂的多。当然,本文覆盖的主题并不全,比如好友推荐、热点跟踪等就没有涉及到。但古人云“窥一斑而见全豹”,希望本文的介绍能帮助大家更好的理解微博这样的社交网络应用。
微博是一个很多人都在用的社交应用。天天刷微博的人每天都会进行着这样几个操作:原创、转发、回复、阅读、关注、@等。其中,前四个是针对短博文,最后的关注和@则针
- Connection reset 连接被重置的解决方法
百合不是茶
java字符流连接被重置
流是java的核心部分,,昨天在做android服务器连接服务器的时候出了问题,就将代码放到java中执行,结果还是一样连接被重置
被重置的代码如下;
客户端代码;
package 通信软件服务器;
import java.io.BufferedWriter;
import java.io.OutputStream;
import java.io.O
- web.xml配置详解之filter
bijian1013
javaweb.xmlfilter
一.定义
<filter>
<filter-name>encodingfilter</filter-name>
<filter-class>com.my.app.EncodingFilter</filter-class>
<init-param>
<param-name>encoding<
- Heritrix
Bill_chen
多线程xml算法制造配置管理
作为纯Java语言开发的、功能强大的网络爬虫Heritrix,其功能极其强大,且扩展性良好,深受热爱搜索技术的盆友们的喜爱,但它配置较为复杂,且源码不好理解,最近又使劲看了下,结合自己的学习和理解,跟大家分享Heritrix的点点滴滴。
Heritrix的下载(http://sourceforge.net/projects/archive-crawler/)安装、配置,就不罗嗦了,可以自己找找资
- 【Zookeeper】FAQ
bit1129
zookeeper
1.脱离IDE,运行简单的Java客户端程序
#ZkClient是简单的Zookeeper~$ java -cp "./:zookeeper-3.4.6.jar:./lib/*" ZKClient
1. Zookeeper是的Watcher回调是同步操作,需要添加异步处理的代码
2. 如果Zookeeper集群跨越多个机房,那么Leader/
- The user specified as a definer ('aaa'@'localhost') does not exist
白糖_
localhost
今天遇到一个客户BUG,当前的jdbc连接用户是root,然后部分删除操作都会报下面这个错误:The user specified as a definer ('aaa'@'localhost') does not exist
最后找原因发现删除操作做了触发器,而触发器里面有这样一句
/*!50017 DEFINER = ''aaa@'localhost' */
原来最初
- javascript中showModelDialog刷新父页面
bozch
JavaScript刷新父页面showModalDialog
在页面中使用showModalDialog打开模式子页面窗口的时候,如果想在子页面中操作父页面中的某个节点,可以通过如下的进行:
window.showModalDialog('url',self,‘status...’); // 首先中间参数使用self
在子页面使用w
- 编程之美-买书折扣
bylijinnan
编程之美
import java.util.Arrays;
public class BookDiscount {
/**编程之美 买书折扣
书上的贪心算法的分析很有意思,我看了半天看不懂,结果作者说,贪心算法在这个问题上是不适用的。。
下面用动态规划实现。
哈利波特这本书一共有五卷,每卷都是8欧元,如果读者一次购买不同的两卷可扣除5%的折扣,三卷10%,四卷20%,五卷
- 关于struts2.3.4项目跨站执行脚本以及远程执行漏洞修复概要
chenbowen00
strutsWEB安全
因为近期负责的几个银行系统软件,需要交付客户,因此客户专门请了安全公司对系统进行了安全评测,结果发现了诸如跨站执行脚本,远程执行漏洞以及弱口令等问题。
下面记录下本次解决的过程以便后续
1、首先从最简单的开始处理,服务器的弱口令问题,首先根据安全工具提供的测试描述中发现应用服务器中存在一个匿名用户,默认是不需要密码的,经过分析发现服务器使用了FTP协议,
而使用ftp协议默认会产生一个匿名用
- [电力与暖气]煤炭燃烧与电力加温
comsci
在宇宙中,用贝塔射线观测地球某个部分,看上去,好像一个个马蜂窝,又像珊瑚礁一样,原来是某个国家的采煤区.....
不过,这个采煤区的煤炭看来是要用完了.....那么依赖将起燃烧并取暖的城市,在极度严寒的季节中...该怎么办呢?
&nbs
- oracle O7_DICTIONARY_ACCESSIBILITY参数
daizj
oracle
O7_DICTIONARY_ACCESSIBILITY参数控制对数据字典的访问.设置为true,如果用户被授予了如select any table等any table权限,用户即使不是dba或sysdba用户也可以访问数据字典.在9i及以上版本默认为false,8i及以前版本默认为true.如果设置为true就可能会带来安全上的一些问题.这也就为什么O7_DICTIONARY_ACCESSIBIL
- 比较全面的MySQL优化参考
dengkane
mysql
本文整理了一些MySQL的通用优化方法,做个简单的总结分享,旨在帮助那些没有专职MySQL DBA的企业做好基本的优化工作,至于具体的SQL优化,大部分通过加适当的索引即可达到效果,更复杂的就需要具体分析了,可以参考本站的一些优化案例或者联系我,下方有我的联系方式。这是上篇。
1、硬件层相关优化
1.1、CPU相关
在服务器的BIOS设置中,可
- C语言homework2,有一个逆序打印数字的小算法
dcj3sjt126com
c
#h1#
0、完成课堂例子
1、将一个四位数逆序打印
1234 ==> 4321
实现方法一:
# include <stdio.h>
int main(void)
{
int i = 1234;
int one = i%10;
int two = i / 10 % 10;
int three = i / 100 % 10;
- apacheBench对网站进行压力测试
dcj3sjt126com
apachebench
ab 的全称是 ApacheBench , 是 Apache 附带的一个小工具 , 专门用于 HTTP Server 的 benchmark testing , 可以同时模拟多个并发请求。前段时间看到公司的开发人员也在用它作一些测试,看起来也不错,很简单,也很容易使用,所以今天花一点时间看了一下。
通过下面的一个简单的例子和注释,相信大家可以更容易理解这个工具的使用。
- 2种办法让HashMap线程安全
flyfoxs
javajdkjni
多线程之--2种办法让HashMap线程安全
多线程之--synchronized 和reentrantlock的优缺点
多线程之--2种JAVA乐观锁的比较( NonfairSync VS. FairSync)
HashMap不是线程安全的,往往在写程序时需要通过一些方法来回避.其实JDK原生的提供了2种方法让HashMap支持线程安全.
- Spring Security(04)——认证简介
234390216
Spring Security认证过程
认证简介
目录
1.1 认证过程
1.2 Web应用的认证过程
1.2.1 ExceptionTranslationFilter
1.2.2 在request之间共享SecurityContext
1
- Java 位运算
Javahuhui
java位运算
// 左移( << ) 低位补0
// 0000 0000 0000 0000 0000 0000 0000 0110 然后左移2位后,低位补0:
// 0000 0000 0000 0000 0000 0000 0001 1000
System.out.println(6 << 2);// 运行结果是24
// 右移( >> ) 高位补"
- mysql免安装版配置
ldzyz007
mysql
1、my-small.ini是为了小型数据库而设计的。不应该把这个模型用于含有一些常用项目的数据库。
2、my-medium.ini是为中等规模的数据库而设计的。如果你正在企业中使用RHEL,可能会比这个操作系统的最小RAM需求(256MB)明显多得多的物理内存。由此可见,如果有那么多RAM内存可以使用,自然可以在同一台机器上运行其它服务。
3、my-large.ini是为专用于一个SQL数据
- MFC和ado数据库使用时遇到的问题
你不认识的休道人
sqlC++mfc
===================================================================
第一个
===================================================================
try{
CString sql;
sql.Format("select * from p
- 表单重复提交Double Submits
rensanning
double
可能发生的场景:
*多次点击提交按钮
*刷新页面
*点击浏览器回退按钮
*直接访问收藏夹中的地址
*重复发送HTTP请求(Ajax)
(1)点击按钮后disable该按钮一会儿,这样能避免急躁的用户频繁点击按钮。
这种方法确实有些粗暴,友好一点的可以把按钮的文字变一下做个提示,比如Bootstrap的做法:
http://getbootstrap.co
- Java String 十大常见问题
tomcat_oracle
java正则表达式
1.字符串比较,使用“==”还是equals()? "=="判断两个引用的是不是同一个内存地址(同一个物理对象)。 equals()判断两个字符串的值是否相等。 除非你想判断两个string引用是否同一个对象,否则应该总是使用equals()方法。 如果你了解字符串的驻留(String Interning)则会更好地理解这个问题。
- SpringMVC 登陆拦截器实现登陆控制
xp9802
springMVC
思路,先登陆后,将登陆信息存储在session中,然后通过拦截器,对系统中的页面和资源进行访问拦截,同时对于登陆本身相关的页面和资源不拦截。
实现方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23