方差分为:样本方差和总体方差;
总体方差计算公式:
实际工作中,
总体均数难以得到时,应用样本统计量代替总体参数,经校正后,样本方差计算公式:
S^2= ∑(X-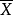 ) ^2 / (n-1)
) ^2 / (n-1)
S^2为样本方差,X为变量,
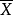 为样本均值,n为样本例数。
为样本均值,n为样本例数。
标准差的平方就是方差;
arr =【2,1,5】
excel上拉数据透视表:
总体方差:2.888889 #=POWER(STDEVP(arr),2)
总体标准(偏)差:1.699673 #=STDEVP(arr)
方差:4.333333 #=VAR(arr) #样本方差
标准(偏)差:2.081666 #=SQRT(VAR(arr)) #样本标准差
python-numpy计算:
import numpy as np
arr = [2, 1, 5]
arr_mean = np.mean(arr)
arr_var = np.var(arr,ddof=1) #样本方差
arr_std = np.std(arr,ddof=1) #样本标准差 ddof就是:n-ddof,ddof默认为0
print("平均值为:%f" % arr_mean)
print("方差为:%f" % arr_var)
print("标准差为:%f" % arr_std)
平均值为:2.666667
方差为:4.333333
标准差为:2.081666
import numpy as np
arr = [2, 1, 5]
arr_mean = np.mean(arr)
arr_var = np.var(arr) #等价于arr_var = np.var(arr,ddof=0) #总体方差
arr_std = np.std(arr,ddof=0) #总体标准差
print("平均值为:%f" % arr_mean)
print("方差为:%f" % arr_var)
print("标准差为:%f" % arr_std)
平均值为:2.666667
方差为:2.888889
标准差为:1.699673
还有一个疑问:上边的一致了 为什么和我手动计算(就是用基础公式计算)的对不上?