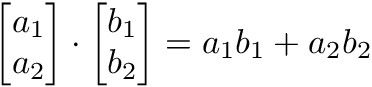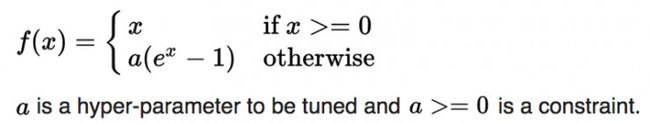导语:在本文中,我们将从卷积神经网络的角度探讨深度学习。
本文编译自《Medical Image Analysis with Deep Learning Part2》,是最近发表的《深度学习下的医学图像分析(一)》的后续文章。雷锋网独家首发。
在《深度学习下的医学图像分析》系列的第一篇文章中,我们介绍了一些使用OpenCV和DICOM图像基础知识进行图像处理的过程。本文,我们将从“卷积神经网络”的角度讨论深度学习。在系列的第三部分,我们将利用Kaggle的肺癌数据库,重新查看肺癌DICOM图像中的关键内容和信息,并且利用Kera开发一个肺癌预测模型。
“卷积神经网络”(CNN)
在了解“卷积神经网络”之前,我们要先知道什么是“卷积”。
何为“卷积”?
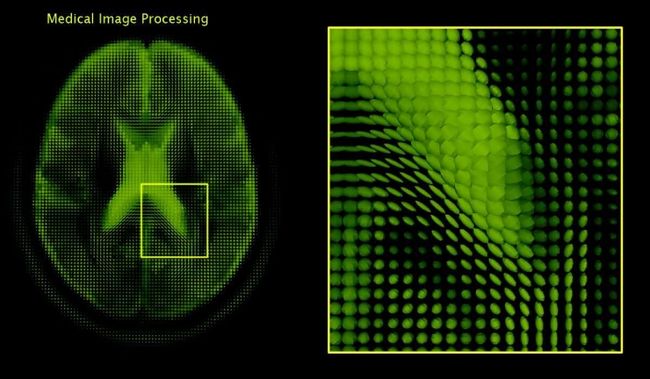
维基百科对“卷积”的定义是:一个关于两个函数的数学运算。这个数学运算将会产生两个原始函数之外的第三个函数,这个函数通常被看作是两个原始函数之一的修正版,实际上是这两个原始函数的点乘式相乘的积分。我们可以简单地将第三个函数理解为“一个矩阵上的滑动窗口函数”。
如上图所示,绿色表示的是滑动窗口,红色的是滑动窗口矩阵,输出的结果是带有卷积特性的矩阵。下图是两个方形脉冲的卷积及其输出结果。
Jeremy Howard在他的MOOC课程里,利用一个Excel表格很好地解释了“卷积”。f和g两个矩阵的卷积输出是第三个矩阵卷积的第一层,也是这两个矩阵的点乘结果。这两个矩阵的点乘结果是下图所示的“标量矩阵”,也是一个数学函数的来源。
两个矩阵的点乘结果
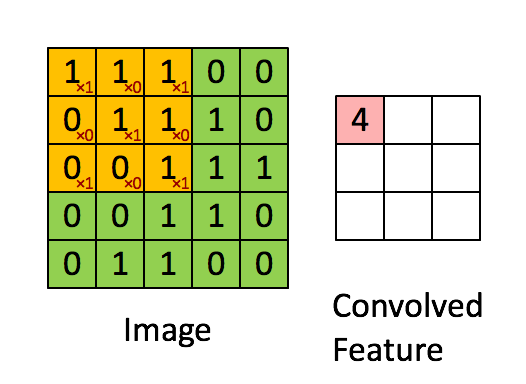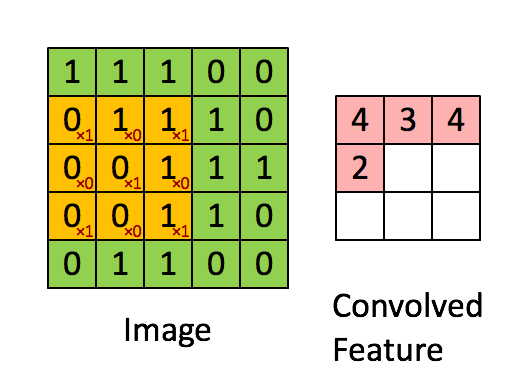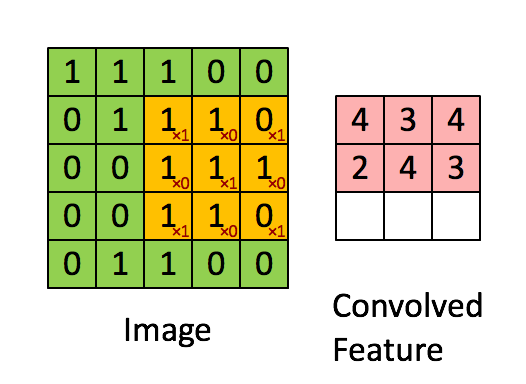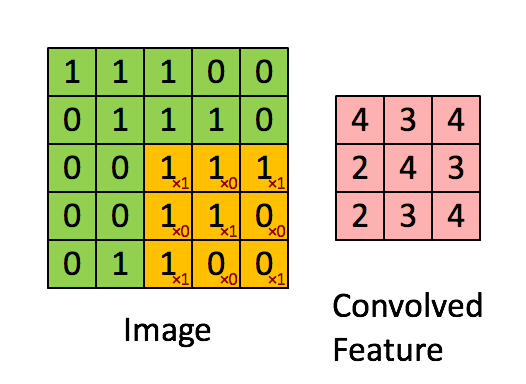
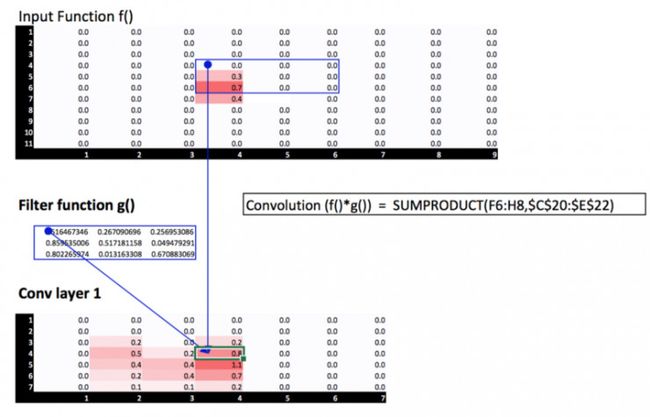
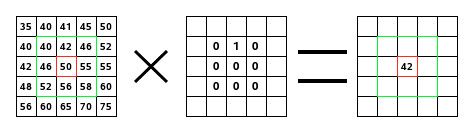
像Jeremy一样,我们也来利用Excel表格。我们输入的矩阵是函数f(),滑动窗口矩阵是函数g()。两个函数的点乘结果是表格中的两个矩阵的和积,如下图所示:
两个矩阵的卷积
接下来,我们把这个规律用到大写字母A的一张图像。大家都知道,所有图像都是由像素构成的。因此,我们输入的矩阵f是“A”,把滑动窗口函数定为任意的矩阵g。然后,我们就得到了两个函数的点乘结果,如下图:
何为“卷积神经网络”?
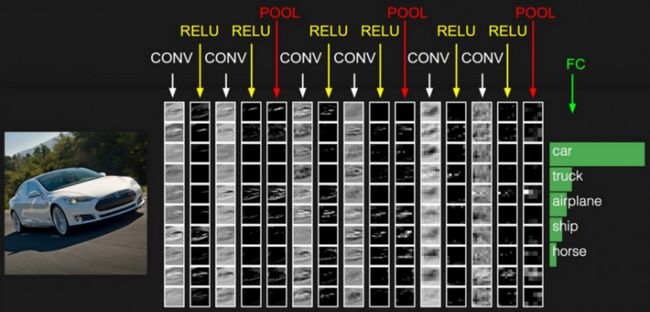
在我看来,一个简单的卷积神经网络CNN是所有层的一个序列。每一层都有一些特定的函数。每个卷积层都是三维的,所以我们用体积来作为度量标准。再进一步,卷积神经网络的每一层都会通过一个可微函数来将激活量转化为另一个,这个函数叫做“激活”或者“转化函数”。
“卷积神经网络”包含的不同实体分别是:输入层、过滤器(或内核)、卷积层、激活层、聚积层、批处理层。虽然这些层的组合排列各异,但是在不同的排列中还是存在一些规律的,给我们提供了不同的深度学习架构。
输入层:一般情况下,我们输入至“卷积神经网络”的通常是一个n维数组。如果是一张图像,我们有彩色通道的三维输入——长、宽、高。
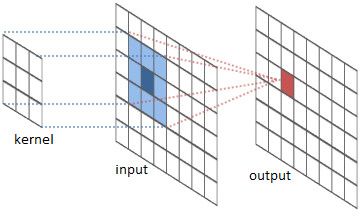
过滤器(或内核):如下图所示,一个过滤器或内核会滑动到图像的所有位置,将一个新像素作为所有像素的加权总和来进行计算。正如上面Excel表格的示例,我们的过滤器g移动到了输入的矩阵f处。
卷积层:输入矩阵的点乘结果与内核共同创造出的新矩阵就是“卷积矩阵”,也被称作“卷积层”。
下面这张非常清晰的视觉图表能够帮助你能更好地了解卷积填充和卷积转置的具体过程:
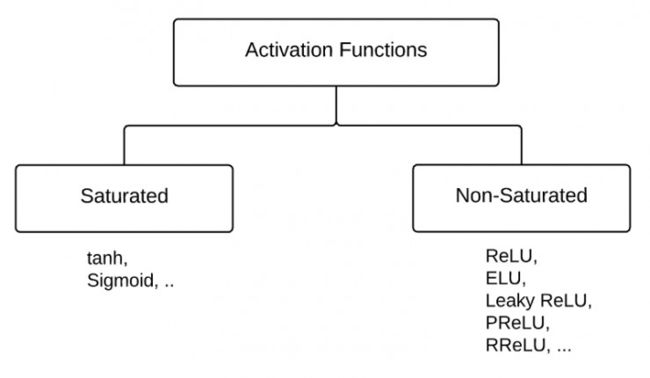
激活层:“激活函数”能分成两类——“饱和激活函数”和“非饱和激活函数”。
sigmoid和tanh是“饱和激活函数”,而ReLU及其变体则是“非饱和激活函数”。使用“非饱和激活函数”的优势在于两点:
1.首先,“非饱和激活函数”能解决所谓的“梯度消失”问题。
2.其次,它能加快收敛速度。
Sigmoid函数需要一个实值输入压缩至[0,1]的范围
σ(x) = 1 / (1 + exp(−x))
tanh函数需要讲一个实值输入压缩至 [-1, 1]的范围
tanh(x) = 2σ(2x) − 1
ReLU
ReLU函数代表的的是“修正线性单元”,它是带有卷积图像的输入x的最大函数(x,o)。ReLU函数将矩阵x内所有负值都设为零,其余的值不变。ReLU函数的计算是在卷积之后进行的,因此它与tanh函数和sigmoid函数一样,同属于“非线性激活函数”。这一内容是由Geoff Hinton首次提出的。
ELUs
ELUs是“指数线性单元”,它试图将激活函数的平均值接近零,从而加快学习的速度。同时,它还能通过正值的标识来避免梯度消失的问题。根据一些研究,ELUs分类精确度是高于ReLUs的。下面是关于ELU细节信息的详细介绍:
Leaky ReLUs
ReLU是将所有的负值都设为零,相反,Leaky ReLU是给所有负值赋予一个非零斜率。Leaky ReLU激活函数是在声学模型(2013)中首次提出的。以数学的方式我们可以表示为:
上图中的ai是(1,+∞)区间内的固定参数。
参数化修正线性单元(PReLU)
PReLU可以看作是Leaky ReLU的一个变体。在PReLU中,负值部分的斜率是根据数据来定的,而非预先定义的。作者称,在ImageNet分类(2015,Russakovsky等)上,PReLU是超越人类分类水平的关键所在。
随机纠正线性单元(RReLU)
“随机纠正线性单元”RReLU也是Leaky ReLU的一个变体。在RReLU中,负值的斜率在训练中是随机的,在之后的测试中就变成了固定的了。RReLU的亮点在于,在训练环节中,aji是从一个均匀的分布U(I,u)中随机抽取的数值。形式上来说,我们能得到以下结果:
下图是ReLU、Leaky ReLU、PReLU和RReLU的比较:
PReLU中的ai是根据数据变化的;Leaky ReLU中的ai是固定的;RReLU中的aji是一个在一个给定的范围内随机抽取的值,这个值在测试环节就会固定下来。
噪声激活函数
这些是包含了Gaussian噪声的激活函数,下图能帮助你了解“噪声”是如何与激活函数相结合的:
聚积层
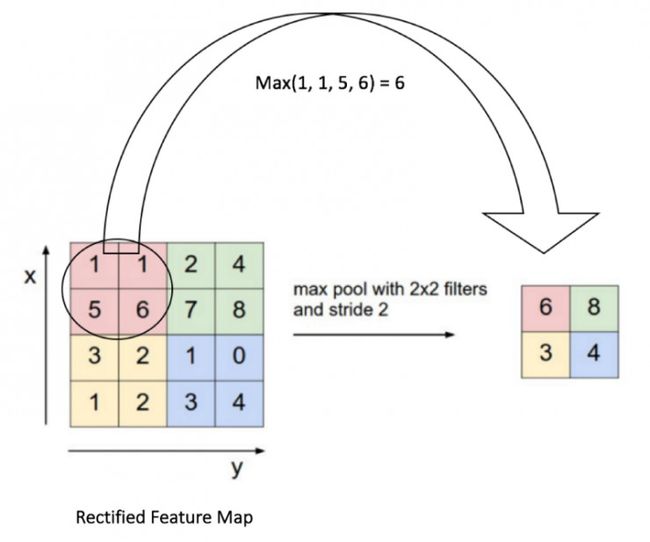
“聚积层”的目的就是通过逐渐缩减矩阵的空间大小,减少参数和网络内计算的数量,进而控制过度拟合。“聚积层”在输入中独立运行,然后利用最大值或平均值的操作来调整输入矩阵的空间大小。“聚积层”最常见的形式就是带有应用于输入的两个样本中的2x2过滤器的“聚积层”。在这种形式中,每一次最大值操作都会取超过4个的最大数量,深度维数保持不变。更常见的“聚积层”如下图:
注意:这里我们把2 x 2窗口移动了两个单元格,然后取每个区域的最大值。
批规范化层
“批规范化”是将每个过渡层,包括激活函数,标准化的有效方法。“批规范化”操作的两个主要优点是:
1.在一个模型中添加“批规范”能够加快训练的速度
2.规范化操作大大降低了少数外围输入对训练的制约影响,同时减少了过度拟合的发生。
Jeremy的网络公开课中有更多关于“批规范化”的细节。
全连接层
“全连接层”是一个传统的“多层感知器”,这个感知器在输出层中使用了一个“柔性最大值激活函数”。顾名思义,“全连接”意味着上一层的每一个神经元都与下一层的每个神经元相连接。一个“柔性最大值函数”是逻辑函数的泛化,该函数将一个任意实值的K维向量转化为一个实值在(0,1)范围之间的K维向量。
“柔性最大值激活函数”一般被用于最后的全连接层,获取实值在0到1之间的概率。现在,我们对“卷积神经网络”中的不同层已经有所了解了,那么具备了这些知识,我们就能建立起肺癌检测所需的深度学习架构了。关于肺癌检测的深度学习架构,我们将在下一篇文章中讨论。
注:文章首发于雷锋网,转载请注明。