数据结构与算法——字符串排序
对于许多排序应用,决定顺序的键都是字符串。下面将学习专门针对字符串类型的排序方法,这些方法比之前学习的通用排序方法(如冒泡、插入、归并等)更高效。
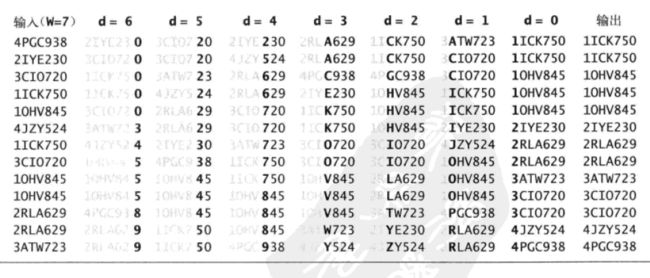
第一类方法是低位优先(Least-Signifcant-Digit First,LSD)的字符串排序方法。这个算法要求被排序的每个字符串长度都相等。它会把字符串当成数字,从字符串的右边开始向左检查字符(相当于从数字的最低位到高位)。
第二类方法是高位优先(MSD)的字符串排序。它不要求被排序的字符串等长,而且不一定需要检查所有的输入就能完成排序。该算法将从左开始向右检查字符(就像通常我们比较字符串那样),使用和快速排序类似的方法将字符串排序。
在学习低位优先的字符串排序时,最好先了解下计数排序和基数排序。上一篇文章中已经有详细介绍了,这里不再赘述。
低位优先的字符串排序LSD
首先待排序的字符串长度均相同,设为W,从右向左以每个字符作为关键字,用计数排序法将字符串排序W次。由于计数排序法是稳定的,所以低位优先的字符串排序能够稳定地将字符串排序。
假设你对计数排序和基数排序都有一定的了解了,这里直接给出代码。
package Chap5;
import java.util.Arrays;
public class LSD {
public static void sort(String[] a, int W) {
// 每位数字范围0~9,基为10
int R = 256;
int N = a.length;
String[] aux = new String[N];
int[] count = new int[R+1];
// 共需要d轮计数排序, 从最后一位开始,符合从右到左的顺序
for (int d = W - 1; d >= 0; d--) {
// 1. 计算频率,在需要的数组长度上额外加1
for (int i = 0; i < N; i++) {
// 使用加1后的索引,有重复的该位置就自增
count[a[i].charAt(d) + 1]++;
}
// 2. 频率 -> 元素的开始索引
for (int r = 0; r < R; r++) {
count[r + 1] += count[r];
}
// 3. 元素按照开始索引分类,用到一个和待排数组一样大临时数组存放数据
for (int i = 0; i < N; i++) {
// 填充一个数据后,自增,以便相同的数据可以填到下一个空位
aux[count[a[i].charAt(d)]++] = a[i];
}
// 4. 数据回写
for (int i = 0; i < N; i++) {
a[i] = aux[i];
}
// 重置count[],以便下一轮统计使用
for (int i = 0; i < count.length; i++) {
count[i] = 0;
}
}
}
public static void main(String[] args) {
String[] a = {"4PGC938", "2IYE230", "3CIO720", "1ICK750", "1OHV845", "4JZY524", "1ICK750", "3CIO720",
"1OHV845", "1OHV845","2RLA629", "2RLA629", "3ATW723"};
LSD.sort(a, 7);
System.out.println(Arrays.toString(a));
}
}
上面程序将打印如下内容
[1ICK750, 1ICK750, 1OHV845, 1OHV845, 1OHV845, 2IYE230, 2RLA629, 2RLA629, 3ATW723, 3CIO720, 3CIO720, 4JZY524, 4PGC938]
我们来看下对这些字符串排序的LSD轨迹。
为什么从右往左以每一位字符为键排序W次就能对字符串排序了呢?试想一种简单情况:如果有两个键,它们的第0位还没有被排序且它们相同,那么字符串中不同的地方就在于已经排序的第1位,出于计数排序的稳定性,它们将一直保持有序;除非未被排序的第1位字符不同,那么已经排序过的字符对于两者的最终顺序是没有意义的,之后的某轮处理会根据更高字符的不同修正这对键的顺序。比如["SC", "SB", "AD"],以第1位字符为键排序后是["SB", "SC", "AD"]对于"SB"和"SC"它们的第0位还没有排序且相同,由于计数排序的稳定,在这种情况下,它们以第0位排序时会保持有序;而对于"SB"和"AD"它们的第0位还没有排序且不同,那么第1位排序的结果就没有意义了,因为对第0位排序后变成["AD", "SB", "SC"],可以看到原来字符串第1位是BD的顺序,排序后变成DB的顺序了。综上:我们的目的是在较高位字符相同的情况下,保持着较低位的顺序;在较高位字符不同的情况下,保证较高位要有序,低位的顺序已经没有意义。
标准的LSD只能处理等长字符串,下面将要学习的是通用的字符串排序方法(字符串的长度不一定相同)。首先来看高位优先的字符串排序MSD。
高位优先的字符串排序MSD
高位优先的字符串排序MSD可以处理不等长的字符串,它是从左向右检查每个字符,统计字符串首字母的频率,并按其来进行归类、排序,然后对归类后的字符串:将所有首字母相同的归为一个子数组,递归地分别对这些子数组排序。精炼点说就是:
- 以首字母来排序,将数组切分成首字母相同的子数组
- 忽略都相同的首字母,递归地排序子数组
在高位优先的字符串排序算法中,要特别注意字符串末尾的情况。我们需要一个标记来判断是否到达字符串末尾,因此在字符集中需要给字符串末尾定义一个位置,而且字符串的末尾应该比任何字符都要小,比如“other”就小于“others”,所以字符串末尾在字符集中对应的整数应该最小。于是我们可以改写String的charAt方法,当索引达到字符串末尾时,返回-1。但是我们的count[]数组索引自然不能是负数,为此,对每个返回的索引都进行加1处理。即1表示第一个字符,2表示第二个字符...0表示字符串末尾。charAt方法如下
private static int charAt(String s, int d) {
if (d < s.length()) {
return s.charAt(d);
} else {
return -1;
}
}
我们将看到,下面的程序中,所有调用charAt方法的地方,后面都会加1,像这样charAt(a[i], d) + 1
由于字符串末尾占用了字符集的一个位置,所以count[]数组也应该多一个额外的位置,数组长度由原来的R+1要变成R+2。
有了这些预备基础,实现MSD就不难了。
package Chap9;
import java.util.Arrays;
public class MSD {
// 基数
private static int R = 256;
// 切换为插入排序的阈值
private static int M = 15;
public static void sort(String[] a) {
int N = a.length;
String[] aux = new String[N];
sort(a, aux, 0, a.length - 1, 0);
}
private static void sort(String[] a, String[] aux, int low, int high, int d) {
// 对于小型数组,切换到插入排序
if (high <= low + M) {
insertSort(a, low, high, d);
return;
}
// 在原来R+1的基础上多加1是因为要将字符串末尾存放到count[1]中, count[0]依然始终为0
int[] count = new int[R + 2];
// 统计频率
for (int i = low; i <= high; i++) {
count[charAt(a[i], d) + 2]++;
}
// 转换成开始索引
for (int r = 0; r < R + 1; r++) {
count[r+1] += count[r];
}
// 数据分类
for (int i = low; i <= high; i++) {
aux[count[charAt(a[i], d) + 1]++] = a[i];
}
// 写回原数组
for (int i = low; i <= high ; i++) {
a[i] = aux[i-low];
}
// 递归的以每个字符为键进行排序
// 实际上每次递归处理的都是首字母相同的子数组,
// [low + count[r], low + count[r+ 1] -1]是首字母都相同的子数组区间
// d+1表示忽略都相同的首字母,从下一个字符开始统计频率 -> 计数排序
for (int r = 0; r < R; r++) {
sort(a, aux, low + count[r], low + count[r+ 1] -1, d + 1);
}
}
private static int charAt(String s, int d) {
if (d < s.length()) {
return s.charAt(d);
} else {
return -1;
}
}
private static void insertSort(String[] a, int low, int high, int d) {
for (int i = low + 1; i <= high; i++) {
// 当前索引如果比它前一个元素要大,不用插入;否则需要插入
if (less(a[i], a[i - 1], d)) {
// 待插入的元素先保存
String temp = a[i];
// 元素右移
int j;
for (j = i; j > low && less(temp, a[j - 1], d); j--) {
a[j] = a[j - 1];
}
// 插入
a[j] = temp;
}
}
}
private static boolean less(String v, String w, int d) {
return v.substring(d).compareTo(w.substring(d)) < 0;
}
public static void main(String[] args) {
String[] a = {"she", "sells", "seashells", "by", "the", "sea", "shore", "the",
"shells", "she", "sells", "are", "surely", "seashells"};
MSD.sort(a);
System.out.println(Arrays.toString(a));
/* Output:
[are, by, sea, seashells, seashells, sells, sells, she, she, shells, shore, surely, the, the]
*/
}
}
可以看到,核心的sort方法其实只是在计数排序的基础上,多加了最后一个for循环而已。看参数列表,count[r]~count[r+1] - 1这个区间表示索引为r的全部字符(它们都相同),区间两端都加上low表示索引为r的字符的开始索引和结束索引(闭区间)。接着d + 1是因为在对子数组排序时,由于首字母都是相同的,所以忽略它对下一个字符统计频率、排序等。
下面的排序过程(假设M=0,不切换排序方法),能帮助你更好地理解这个算法。可以看到low和high之间首字母都是相同的,加黑的字符正是第d+1位正在被排序的字符。
上面的实现中,有一个专为字符串准备的插入排序,当被切分的数组长度很小时(比如只有十几个元素),会切换到插入排序直接对字符串进行排序。同时为了避免重复检查已知相同的字符,也改写了less方法,对于前d个字符都相同的字符串,将直接从索引d处开始比较。
对小型数组的特殊处理是必须的。和快速排序一样,这种递归地切分子数组的方法会产生大量微型数组。而对于每个子数组都需要创建一个有258个元素的count[]并将频率转换为索引。这种代价比其他排序方法要高很多,如果使用的是16位的Unicode字符集(R=65535),排序过程可能会减慢上千倍。因此将小数组切换成插入排序对于高位优先的字符串排序是必须的。
MSD对于含有大量等值键的子数组排序会很慢,如果相同的字符串太多,切换排序方法将不会被调用。最坏情况是待排序的所有字符串全都相等,此时low和high一直保持原来的值(low=0, hgih=a.length - 1),不会切换到插入排序,而且对于相同的字符串,递归排序将检查所有的字符。
MSD基于计数排序,在切换排序方法时使用插入排序,所以总的来说高位优先的字符串排序是稳定的。
三向字符串快速排序
还记得三向切分的快速排序吗?我们可以利用其思想,将字符串数组切分成三个子数组:一个含有所有首字母小于切分字符的子数组,一个含有所有首字母等于切分字符的子数组,一个含有所有首字母大于切分字符的子数组。然后递归地对这三个数组排序,要注意对于所有首字母等于切分字符的子数组,在递归排序时应该忽略首字母(就像MSD中那样)。
对照三向切分的快速排序代码,只需稍作修改就能实现三向字符串快速排序。
package Chap5;
import java.util.Arrays;
public class Quick3String {
// 切换为插入排序的阈值
private static int M = 15;
public static void sort(String[] a) {
sort(a, 0, a.length - 1, 0);
}
private static void sort(String[] a, int low, int high, int d) {
if (high <= low + M) {
insertSort(a, low, high, d);
return;
}
int lt = low;
int gt = high;
int i = low + 1;
// 切分字符v是a[low]的第d个字符
int v = charAt(a[low], d);
while (i <= gt) {
int t = charAt(a[i], d);
if (t < v) {
swap(a, lt++, i++);
} else if (t > v) {
swap(a, i, gt--);
} else {
i++;
}
}
// 现在a[lo..lt-1] < v=a[lt..gt] < a[gt+1..high]成立
// 切分元素相同的数组不会被递归算法访问到,对其左右的子数组递归排序
sort(a, low, lt - 1, d);
// 所有首字母与切分字符相等的子数组,递归排序,像MSD那样要忽略都相同的首字母
if (v >= 0) {
sort(a, lt, gt, d+ 1);
}
sort(a, gt + 1, high, d);
}
private static void swap(String[] a, int p, int q) {
String temp = a[p];
a[p] = a[q];
a[q] = temp;
}
private static int charAt(String s, int d) {
if (d < s.length()) {
return s.charAt(d);
} else {
return -1;
}
}
private static void insertSort(String[] a, int low, int high, int d) {
for (int i = low + 1; i <= high; i++) {
// 当前索引如果比它前一个元素要大,不用插入;否则需要插入
if (less(a[i], a[i - 1], d)) {
// 待插入的元素先保存
String temp = a[i];
// 元素右移
int j;
for (j = i; j > low && less(temp, a[j - 1], d); j--) {
a[j] = a[j - 1];
}
// 插入
a[j] = temp;
}
}
}
private static boolean less(String v, String w, int d) {
return v.substring(d).compareTo(w.substring(d)) < 0;
}
public static void main(String[] args) {
String[] a = {"she", "sells", "seashells", "by", "the", "sea", "shore", "the",
"shells", "she", "sells", "are", "surely", "seashells"};
Quick3String.sort(a);
System.out.println(Arrays.toString(a));
}
}
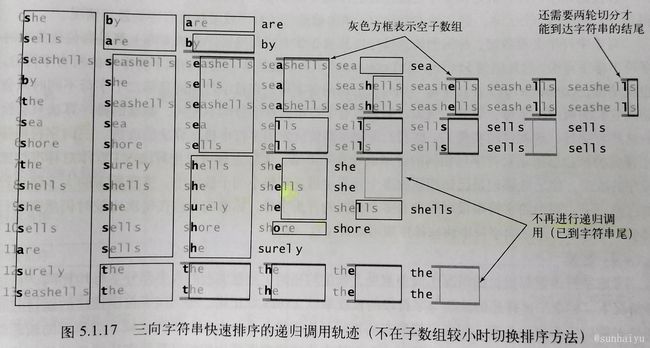
三向字符串快速排序的递归调用轨迹如下图所示。
和MSD一样,在处理小数组时切换到了插入排序,尽管它在三向切分的字符串快速排序的重要性远不及在MSD中的重要性高。三向切分的快速排序使用子数组的第一个元素作为切分点,三向切分的字符串快速排序使用子数组的第一个字符串的第d个字符作为切分字符。然后在递归对子数组排序时,相比三向切分的快速排序,三向切分的字符串快速排序多了这么一个判断,这句的意思是只要还没到字符串的末尾(v = -1说明到达,其余均未到达),所有首字母与切分字符相等的子数组也需要递归排序,不过要像MSD那样,忽略掉相同的首字母,处理下一个字符。
if (v >= 0) {
sort(a, lt, gt, d+ 1);
}
MSD可能会创建大量(空)子数组,而三向字符串快速排序只将数组切分为三部分。因此三向字符串快速排序能很好处理等值键、有较长公共前缀的键、取值范围较小的键和小数组。而且三向字符串快速排序不需要额外的空间,MSD就需要count[]和aux[],这些都是它优于MSD的地方。
下表总结了各种字符串排序算法的性能特点。
by @sunhaiyu
2017.11.22