A 计划日
题意:已知李明在YYYY年MM月DD日星期W订了学习计划,现在想看看李明N天后的完成情况和个人总结,你能告诉我那天的日期和星期几吗?
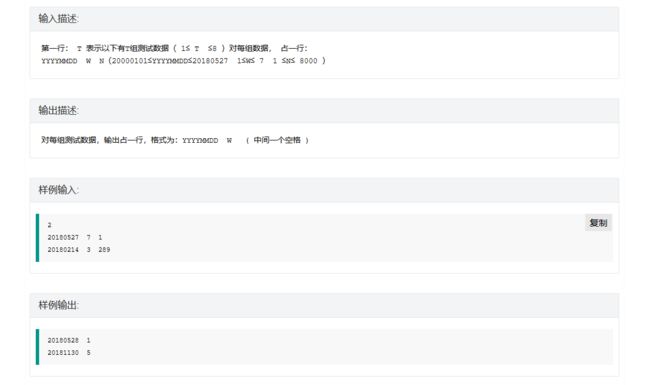
模拟日期计算;
计算星期可以用基姆拉尔森公式
//中国的星期 结果要+1
int Day(int y,int m,int d)
{
if(m==1 || m==2) m+=12,y-=1;
return (d+2*m+3*(m+1)/5+y+y/4-y/100+y/400+1)%7;
}AC代码
#include
using namespace std;
int t;
bool isLeap(int year){
if(year %4 == 0 && year%100!=0 || year%400== 0){
return true;
}
return false;
}
int main(){
cin>>t;
while(t--){
int year,ta,tb,tc,td,w,n,month,day;
scanf("%4d%1d%1d%1d%1d %d %d",&year,&ta,&tb,&tc,&td,&w,&n);
month = ta*10 + tb;
day = tc*10 + td;
if(w==7) w=0;
for(int i=1;i<=n;i++){
if(month == 12){
if(day==31){
year++;
month = 1;
day = 1;
}else{
day++;
}
}else if(month == 1 || month == 3 || month == 5 || month == 7 || month == 8 || month == 10){
if(day == 31){
month++;
day = 1;
}else{
day++;
}
}else if(month == 4 || month == 6 || month == 9 || month == 11){
if(day == 30){
month++;
day = 1;
}else{
day++;
}
}else if(month == 2){
if(isLeap(year)){
if(day == 29){
month++;
day = 1;
}else{
day++;
}
}else{
if(day == 28){
month++;
day = 1;
}else{
day++;
}
}
}
w = (w+1)%7;
}
printf("%d",year);
if(month<10){
printf("0%d",month);
}else{
printf("%d",month);
}
if(day<10){
printf("0%d ",day);
}else{
printf("%d ",day);
}
if(w==0) w = 7;
printf("%d\n",w);
}
return 0;
} B 治安管理
题意:YYH大型活动将在[S,F)这段时间举行,现要求活动期间任何时刻巡逻的警察人数不少于M人。公安机关将有N名警察在维护活动的安全,每人巡逻时间为[ai,bi)。请你检查目前的值班安排,是否符合要求。若满足要求,输出YES,并输出某个时刻同时巡逻的最多人数;若不满足要求,输出NO,并输出某个时刻同时巡逻的最少人数。
暴力可以过;数据如果再复杂点,可以用差分求解区间问题。
AC代码
#include
using namespace std;
int t;
const int maxn = 1e6+5;
int n,m,s,f;
int p[maxn];
int q[maxn];
int a[maxn];
int main(){
cin>>t;
while(t--){
memset(a,0,sizeof(a));
memset(p,0,sizeof(p));
memset(q,0,sizeof(q));
cin>>n>>m>>s>>f;
for(int i=1;i<=n;i++) cin>>p[i];
for(int i=1;i<=n;i++) cin>>q[i];
for(int i=1;i<=n;i++){
for(int j=p[i];j= a[i]) mint = a[i];
if(maxt <= a[i]) maxt = a[i];
}
if(mint == 0x3f3f3f3f) mint = 0;
if(mint C 山区修路
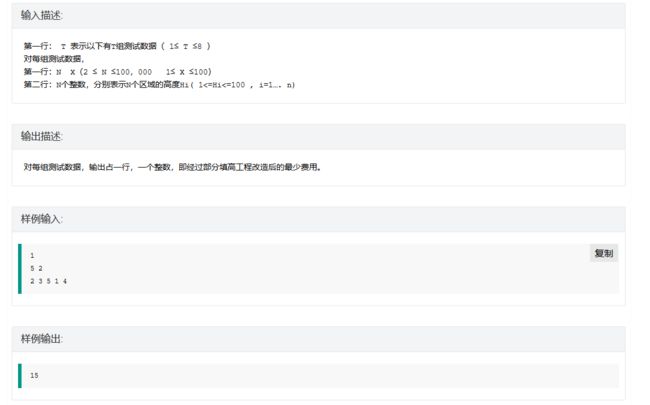
最近,HB省决定修一条从YC市通往SNJ风景区的高速公路。经过勘测分析,途中需要经过高度分别为H1,H2,……,Hn的N个山区。由于高低不平,除正常的修路开支外,每段还要多出高度差|Hi - Hi-1|*X万元的斜坡费用。Dr. Kong 决定通过填高一些区域的高度来降低总的费用。当然填高也是需要一些费用的。每填高Y单位,需要付出Y2万元费用。
你能否帮Dr. Kong做出一个规划,通过部分填高工程改造,使得总的费用降下来。
思路:线性dp,开始想用一维dp,发现一维没法做啊,前后两个山区都影响当前状态。应该用二维dp[i][j] 表示第i个山区在高度为j时的最小费用。
D 求XF+闭包
题意:前面大段都不用看
已知 F 是关系模式R(U)上的函数依赖集,利用Armstrong公理系统可以推导出更多的函数依赖。设X是属性集U={ A1,A2, ……, An} 的子集, 定义X关于F的闭包XF+
XF+={ Ai | 若X->Ai可以通过Armstrong公理导出}
对于给定的U , F ,X, 请求出XF+
意思就是:若X包含S,就将T加入X
思路:我是用字符串string直接做的,string.find()来查找
AC代码,南阳oj过不了,郑轻可以过,有时间再补题吧
#include
using namespace std;
int t;
set se;
int main(){
cin>>t;
while(t--){
int n,m,k;
cin>>n>>m>>k;
string u,x;
cin>>u;
cin>>x;
for(int i=1;i<=k;i++){
string s;
string t;
cin>>s;
cin>>t;
bool flag = true;
int len = s.length();
for(int j=0;j::iterator it = se.begin();
while(it!=se.end()){
cout<<*it;
it++;
}
cout< E 物流配送
http://nyoj.top/web/contest/problem/cid/103/num/E
听说是最小费用最大流
但是我没做过题,想学的时候再补。
F Gene mutation
http://nyoj.top/web/contest/problem/cid/103/num/F
一道简单英文题
思路1:从X数组出发 枚举起点,看看x[i] - y[1]的长度下,x数组中是否都包含Y[j] + x[i] - y[1]
思路2:从Y数组出发,枚举加减的数量,在X中查找,如果存在Y的每一个元素,则记为一种方案。
我用思路2做的没过,有时间再用思路1做
G Checkpoints
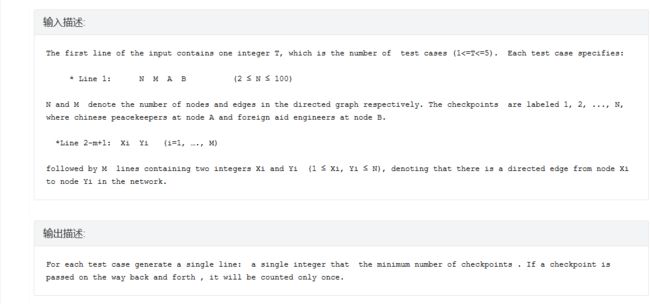
Chinese peacekeepers are going to the town of Kerver to seek Chinese foreign aid engineers.
The military map shows that there are many checkpoints in the war zone. It can be modeled as a directed graph: nodes represent checkpoints , and edges represents the roads. The goal is that the less peacekeepers pass the checkpoints, the safer it will be.
做ACM的英文题,前几段落都可以不读,题意重点在最后两段。。
这题是求单源点最短路
用dijkstra跑一遍
南阳OJ过不了,郑轻可以AC。。。有时间再查问题
#include
using namespace std;
int t;
int A,B;
const int MAX_N = 105;
const int MAX_M = 100000;
const int inf = 0x3f3f3f3f;
struct edge {
int v, w, next;
} e[MAX_M];
int p[MAX_N], eid, n,m;
void mapinit() {
memset(p, -1, sizeof(p));
eid = 0;
}
void insert(int u, int v, int w) { // 插入带权有向边
e[eid].v = v;
e[eid].w = w;
e[eid].next = p[u];
p[u] = eid++;
}
void insert2(int u, int v, int w) { // 插入带权双向边
insert(u, v, w);
insert(v, u, w);
}
int dist[MAX_N]; // 存储单源最短路的结果
bool vst[MAX_N]; // 标记每个顶点是否在集合 U 中
struct node {
int u;
int dist;
node(int _u, int _dist) : u(_u), dist(_dist) {}
bool operator < (const node &x) const {
return dist > x.dist;
}
}; // 记录点的结构体
bool dijkstra(int s) {
// 初始化 dist、小根堆和集合 U
memset(vst, 0, sizeof(vst));
memset(dist, 0x3f, sizeof(dist));
priority_queue min_heap;
dist[s] = 0;
min_heap.push(node(s, 0));
while (!min_heap.empty()){
// 获取堆顶元素,并将堆顶元素从堆中删除
int v = min_heap.top().u;
min_heap.pop();
if (vst[v]) {
continue;
}
vst[v] = true;
// 进行和普通 dijkstra 算法类似的松弛操作
for (int j = p[v]; j != -1; j = e[j].next) {
int x = e[j].v;
if (!vst[x] && dist[v] + e[j].w < dist[x]) {
dist[x] = dist[v] + e[j].w;
min_heap.push(node(x, dist[x]));
}
}
}
return true;
}
int main(){
cin>>t;
while(t--){
cin>>n>>m>>A>>B;
mapinit();
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
insert(u,v,1);
}
dijkstra(A);
cout< H Attack City and Capture Territory
Who breaks through the last firepower point, he will win the city.
Because of limited weaponry, weapons of each side can only attack one firepower at a time. But they can control whether completely destroy this firepower point or weaken the strength of firepower point.
Liu_B has a strong think-tank. After calculation, he finds out who will attack first , who will more likely win the city .
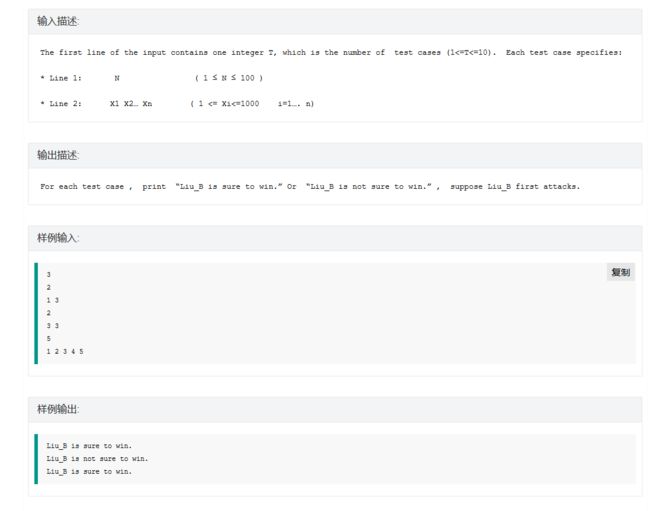
从最后两段中理解题意,是一个直接的nim博弈。
AC代码
#include
using namespace std;
int t;
int a[1010];
int n;
int main(){
cin>>t;
while(t--){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int res = 0;
for(int i=1;i<=n;i++) res^=a[i];
if(res){
puts("Liu_B is sure to win.");
}else{
puts("Liu_B is not sure to win.");
}
}
return 0;
}