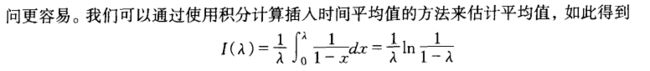目录
- 1.查找问题
- 2.表(数组、链表)
2.1 顺序搜索(未排序的:线性时间)
2.2 二分查找(排序好的:对数时间) - 3.散列表(常数时间)
3.1 直接寻址表
3.2 散列表
3.2.1 链接法解决冲突
3.3 散列函数
3.3.1 除法散列法
3.3.2 乘法散列法
3.3.3 全域散列法(随机选择一个散列函数,在某次计算中一直用h,不要理解错了)
3.4 开放寻址法
3.5 完全散列
3.6 可扩散列 - 4.二叉搜索树
- 5.平衡查找树
1.查找问题
给定一个n个元素的序列或集合,在该序列或集合里面查找一个特定的元素
2.表(数组、链表)
2.1 顺序搜索(未排序的:线性时间)
2.2 二分查找(排序好的:对数时间)
时间分析:
可得:T(n) = Θ(lgn)
3.散列表(常数时间)
如果空间允许,可以提供一个数组,为每个可能的关键字保留一个位置,以利用直接寻址的优势。
当实际存储的关键字数目比全部可能关键字总数要小时,采用散列表。在散列表里,根据关键字计算出相应的下标。
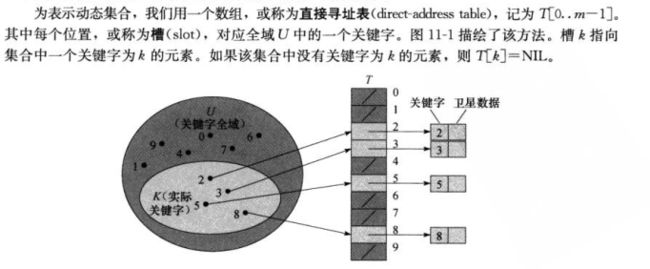
3.1 直接寻址表
当关键字的全域U比较小时,直接寻址是一种简单有效的技术。
3.2 散列表
1)全域U很大
2)实际存储的关键字集合K相对U来说很小
因此,将散列表的存储需求降至为Θ(|K|)
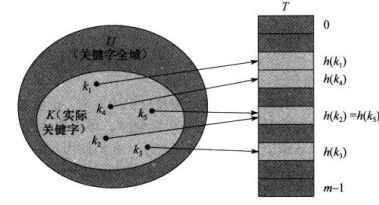
利用散列函数h,将关键字的全域U映射到散列表T[0..m-1]的槽位上:
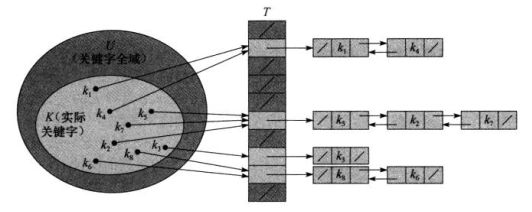
3.2.1 链接法解决冲突
一个问题:两个关键字可能映射到同一个槽中,称之为冲突。
链接法:把散列到同一槽中的所有元素都放在一个链表中。
链接法散列的分析:
装载因子:n个元素、m个槽位的散列表T,装载因子为n/m
最坏情况:所有的n个关键字都散列到同一个槽中,查找时间为Θ(n)
散列方法的平均性能依赖于所选取的散列函数h,将所有的关键字集合分布在m个槽位上的均匀程度。
简单均匀散列假设:假定任何一个给定元素等可能地散列到m个槽位中的任何一个,且与其他元素被散列到什么位置上无关。
上面的分析意味着:如果散列表中槽数至少与表中的元素数成正比,则有n=O(m),从而α=n/m=O(1),所以查找操作平均需要常数时间。
3.3 散列函数
1)用除法进行散列——启发式方法
2)用乘法进行散列——启发式方法
3)全域散列——随机技术
一个好的散列函数应(近似的)满足简单均匀假设:每个关键字都被等可能地散列到m个槽位中的任何一个,并与其他关键字已散列到哪个槽位无关。
多数散列函数都假定关键字的全域为自然数集,如果不是,就要找到一种方法将它们转换为自然数。
3.3.1 除法散列法
h(k) = k mod m
当应用除法散列时,要避免选择m的某些值。m不应为2的幂。
一个不太接近2的整数幂的素数,常常是m的一个较好的选择。
m不应为2的幂,因为如果m=2ⁿ,则h(k)就是k的n个最低位数字。
除非已知各种最低n位的排列形式为等可能,
否则在设计散列函数时,最好考虑关键字的所有位。
例子:
假定分配一张散列表并用链接法解决冲突,表中大约存放n=2000个字符串,
其中每个字符有8位。如果不介意一次不成功的查找需要平局检查3个元素,
这样分配散列表的大小为m = 701.
因为701接近2000/3,并且不接近2的任何次幂的素数。
3.3.2 乘法散列法
3.3.3 全域散列法(随机选择一个散列函数,在某次计算中一直用h,不要理解错了)
任何一个特定的散列函数都可能出现将n个关键字全部散列到同一个槽中。唯一有效的改进方法是随机地选择散列函数,使之独立于要存储的关键字,这种方法称之为全域散列。
全域散列函数的定义:
全域散列函数类的平均性态是比较好的:
全域散列法:通过在运行时聪明地随机选择散列函数,就可以确保每一个操作序列都具有良好的平均情况运行时间。
设计一个全域散列函数类(数论相关)
3.4 开放寻址法
所有的元素都存放在散列表里面。导致装载因子α不会超过1.
1)探查probe
假定不会删除元素:
删除(必须删除时,一般采用链接法来解决冲突):
均匀散列假设:每个关键字的探查序列等可能地为m!种排列的任一种。
2)线性探查
若一个空槽前有i个满的槽时,该空槽为下一个将被占用的概率(i+1)/m。
证明:若T[h'(k)]若等于这个i个槽或者该空槽时,该空槽都将被填满,因此概率为(i+1)/m
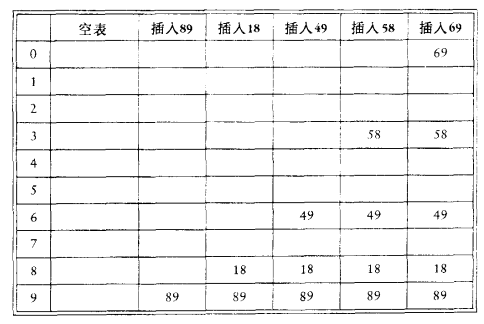
使用线性探查插入关键字{89,18,49,58,69}:
第一次冲突:49,放到下一个空闲地址0
第二次冲突:58,与18,89,49冲突
第三次冲突:69,与89,49,58冲突
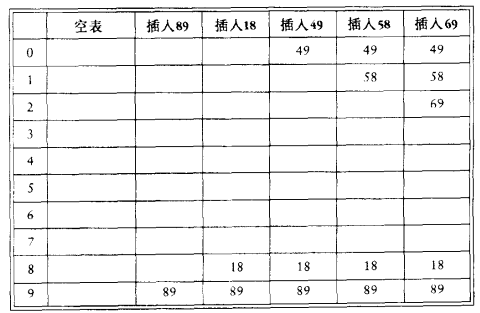
3)二次探查(平方探查)
选择二次形式为:i²
第一次冲突:49
第二个冲突:58,与18,89冲突(比线性查找少)
第三个冲突:69,与89,48冲突(比线性查找少)
这里证明的核心是:
1)从i取值0..ceil(TableSize/2) 个备选中,T[h'(k) + i²]均不相同(超过一半各不相同)
2)因此,若此时表中至少有一半是空的时候,则必有一个空位可以插入
注意:表的大小是素数非常重要
1)如果表示16,那么备选单元只能在距离散列值1,4,9
因此i取值0-15,i²mod16取值为(0, 1, 4, 9, 16:1, 25:9, 36:4, 49:1, 64:0 ... )
备选单元锐减
2)如果表的大小是4k+3,且使用二次型为±i²,那么整个表均可被探测到
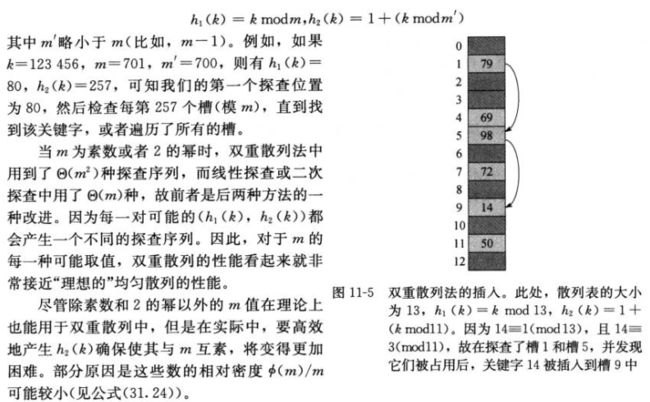
4)双重散列
h2(k)的选择:
a.函数一定不能算得0值
b.保证所有单元都能被探测到
如下例子中选择h2(k) = R-(k mod R),T为小于TableSize的素数,选择R = 7.
第一次冲突:49, (7 - (49 mod 7)) = 7
第二个冲突:58, (7 - (58 mod 7)) = 5
第三个冲突:69, (7 - (69 mod 7)) = 1
这三个元素分别只有一个冲突,比二次和一次都要少很多
5)开放寻址散列的分析
另一种理解方法:
一次不成功查找中探查的期望次数,正是知道我们找到一个空单元的探查的期望次数。
由于空单元所占的份额是1-α,因此要探测的单元数是1/(1-α)
另一种理解方法:
6)再散列
对于使用平方探测的开放定址散列法,如果表的元素填的太满,那么操作的运行时间将开始消耗过长,且插入操作可能失败。
再散列法:一种解决方法是建立另外一个大约两倍大的表(且使用一个相关的新的散列函数),扫描整个原始散列表,计算每个(未删除)元素的新散列值并将其插入到新表中。
由于不是经常发生,因此实际效果根本没有这么差。
实现方法:当表到达某一个装填因子时进行再散列。