前言
1 、排序的概念
排序是计算机内经常进行的一种操作,其目的是将一组“无序”的记录序列调整为“有序”的记录序列。
排序分为内部排序和外部排序。
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
反之,若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
2 、排序分类
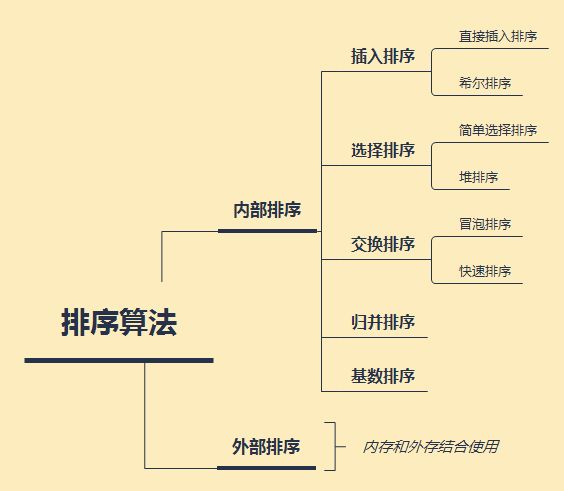
八大排序算法均属于内部排序。如果按照策略来分类,大致可分为:交换排序、插入排序、选择排序、归并排序和基数排序。如下图所示:
3 、算法分析
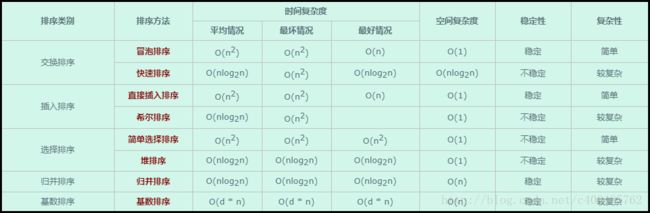
下表给出各种排序的基本性能,具体分析请参看各排序的详解:
一、插入排序
插入排序分为两种:直接插入排序和希尔排序
直接插入排序
基本思想:
直接插入排序的核心思想就是:将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过。
因此,从上面的描述中我们可以发现,直接插入排序可以用两个循环完成:
- 第一层循环:遍历待比较的所有数组元素
- 第二层循环:将本轮选择的元素与已经排好序的元素相比较。
如果:selected > ordered,那么将二者交换
def insert_sort(array):
for i in range(len(array)):
for j in range(i):
if array[i] < array[j]:
array.insert(j, array.pop(i))
break
return array
希尔排序
基本思想:
将数组列在一个表中并对列分别进行插入排序,重复这过程,不过每次用更长的列(步长更长了,列数更少了)来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身还是使用数组进行排序。
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
def shell_sort(alist):
n = len(alist)
# 初始步长
gap = n // 2
while gap > 0:
# 按步长进行插入排序
for i in range(gap,n):
j = i
# 原地插入排序,之前的插入排序另辟空间存储的
while j>=gap and alist[j-gap] > alist[j]:
alist[j-gap], alist[j] = alist[j], alist[j-gap]
j -= gap
# 得到新的步长
gap = gap //2
return alist
最坏情况O(n^2) ,平均O(nlog(n))~O(n2),最好O(n1.3) ,不稳定。
二、选择排序
选择排序分为简单选择排序和堆排序
简单选择排序
基本思想:
比较+交换。
- 从待排序序列中,找到关键字最小的元素;
- 如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
- 从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。
因此我们可以发现,简单选择排序也是通过两层循环实现。
- 第一层循环:依次遍历序列当中的每一个元素
- 第二层循环:将遍历得到的当前元素依次与余下的元素进行比较,符合最小元素的条件,则交换。
def select_sort(array):
for i in range(len(array)):
x = i # min index
for j in range(i, len(array)):
if array[j] < array[x]:
x = j
array[i], array[x] = array[x], array[i]
return array
堆排序
基本思想:
堆排序可以按照以下步骤来完成:
- 首先将序列构建成为大顶堆;
(这样满足了大顶堆那条性质:位于根节点的元素一定是当前序列的最大值) - 取出当前大顶堆的根节点,将其与序列末尾元素进行交换;
(此时:序列末尾的元素为已排序的最大值;由于交换了元素,当前位于根节点的堆并不一定满足大顶堆的性质) - 对交换后的n-1个序列元素进行调整,使其满足大顶堆的性质;
- 重复2.3步骤,直至堆中只有1个元素为止
堆排序的时间复杂度分为两个部分一个是建堆的时候所耗费的时间,一个是进行堆调整的时候所耗费的时间。而堆排序则是调用了建堆和堆调整。
建堆是一个线性过程,从len/2-0一直调用堆调整的过程,相当于o(h1)+o(h2)+…+o(hlen/2)这里的h表示节点深度,len/2表示节点深度,对于求和过程,结果为线性的O(n) 堆调整为一个递归的过程,调整堆的过程时间复杂度与堆的深度有关系,相当于lgn的操作。 因为建堆的时间复杂度是O(n),调整堆的时间复杂度是lgn,所以堆排序的时间复杂度是O(nlgn)。
def heap_sort(array):
def heap_adjust(parent):
child = 2 * parent + 1 # left child
while child < len(heap):
if child + 1 < len(heap):
if heap[child + 1] > heap[child]:
child += 1 # right child
if heap[parent] >= heap[child]:
break
heap[parent], heap[child] = \
heap[child], heap[parent]
parent, child = child, 2 * child + 1
heap, array = array.copy(), []
for i in range(len(heap) // 2, -1, -1):
heap_adjust(i)
while len(heap) != 0:
heap[0], heap[-1] = heap[-1], heap[0]
array.insert(0, heap.pop())
heap_adjust(0)
return array
三、归并排序
基本思想:
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个典型的应用。它的基本操作是:将已有的子序列合并,达到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
归并排序其实要做两件事:
分解----将序列每次折半拆分
合并----将划分后的序列段两两排序合并
因此,归并排序实际上就是两个操作,拆分+合并
合并:
L[first...mid]为第一段,L[mid+1...last]为第二段,并且两端已经有序,现在我们要将两端合成达到L[first...last]并且也有序。
首先依次从第一段与第二段中取出元素比较,将较小的元素赋值给temp[]
重复执行上一步,当某一段赋值结束,则将另一段剩下的元素赋值给temp[]
此时将temp[]中的元素复制给L[],则得到的L[first...last]有序
分解:
在这里,我们采用递归的方法,首先将待排序列分成A,B两组;然后重复对A、B序列
分组;直到分组后组内只有一个元素,此时我们认为组内所有元素有序,则分组结束。
def merge_sort(nums): # 变成二次树
if len(nums) == 1:
return nums
mid = len(nums) // 2
left = nums[:mid]
right = nums[mid:]
a = merge_sort(left)
b = merge_sort(right)
return merge(a, b)
def merge(left, right): # 整合排序
c = []
j = k = 0
while len(left) > j and len(right) > k:
if left[j] <= right[k]:
c.append(left[j])
j += 1
else:
c.append(right[k])
k += 1
if j == len(left):
for i in right[k:]:
c.append(i)
else:
for i in left[j:]:
c.append(i)
return c
四、基数排序
基本思想:
通过序列中各个元素的值,对排序的N个元素进行若干趟的“分配”与“收集”来实现排序。
分配:我们将L[i]中的元素取出,首先确定其个位上的数字,根据该数字分配到与之序号相同的桶中
收集:当序列中所有的元素都分配到对应的桶中,再按照顺序依次将桶中的元素收集形成新的一个待排序列L[ ]
对新形成的序列L[]重复执行分配和收集元素中的十位、百位...直到分配完该序列中的最高位,则排序结束
根据上述“基数排序”的展示,我们可以清楚的看到整个实现的过程
def radix_sort(array):
bucket, digit = [[]], 0
while len(bucket[0]) != len(array):
bucket = [[], [], [], [], [], [], [], [], [], []]
for i in range(len(array)):
num = (array[i] // 10 ** digit) % 10
bucket[num].append(array[i])
array.clear()
for i in range(len(bucket)):
array += bucket[i]
digit += 1
return array
五、交换排序
交换排序分为两种:冒泡排序和快速排序
冒泡排序
基本思想:
- 将序列当中的左右元素,依次比较,保证右边的元素始终大于左边的元素;
( 第一轮结束后,序列最后一个元素一定是当前序列的最大值;) - 对序列当中剩下的n-1个元素再次执行步骤1。
- 对于长度为n的序列,一共需要执行n-1轮比较
(利用while循环可以减少执行次数)
def bubble_sort(array):
for i in range(len(array)):
for j in range(i, len(array)):
if array[i] > array[j]:
array[i], array[j] = array[j], array[i]
return array
快速排序
基本思想:挖坑填数+分治法
从序列当中选择一个基准数(pivot)
在这里我们选择序列当中第一个数最为基准数
将序列当中的所有数依次遍历,比基准数大的位于其右侧,比基准数小的位于其左侧
重复步骤1.2,直到所有子集当中只有一个元素为止。
用伪代码描述如下:
1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2.j--由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
4.再重复执行2,3二步,直到i==j,将基准数填入a[i]中
def quick_sort(array):
sys.setrecursionlimit(10 ** 8)
def recursive(begin, end):
if begin > end:
return
l, r = begin, end
pivot = array[l]
while l < r:
while l < r and array[r] > pivot:
r -= 1
while l < r and array[l] <= pivot:
l += 1
array[l], array[r] = array[r], array[l]
array[l], array[begin] = pivot, array[l]
recursive(begin, l - 1)
recursive(r + 1, end)
recursive(0, len(array) - 1)
return array
六、总结
- (1)若n较小(如n≤50),可采用直接插入或直接选择排序。
当记录规模较小时,直接插入排序较好;否则如果直接选择移动的记录数少于直接插人,应选直接选择排序为宜。 - (2)若文件初始状态基本有序(指正序),则应选用直接插入、冒泡或随机的快速排序为宜;
- (3)若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序。
快速排序是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
若要求排序稳定,则可选用归并排序。但本章介绍的从单个记录起进行两两归并的排序算法并不值得提倡,通常可以将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子文件,然后再两两归并之。因为直接插入排序是稳定的,所以改进后的归并排序仍是稳定的。
七、参考文献
[1] 李春葆. 数据结构教程[M].北京市:清华大学出版社,2013.
[2] li563868273.各种排序的比较和使用场景分析.CSDN,2016.
[3] LeeLom. 数据结构常见的八大排序算法.,2016.
[4] woider. Python 八大排序算法速度比较.博客园,2016.