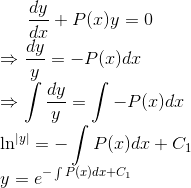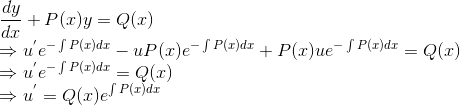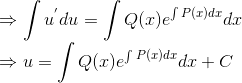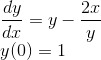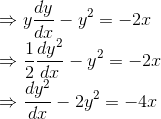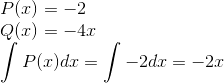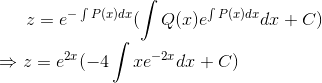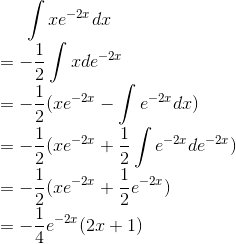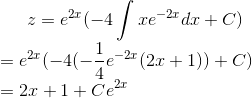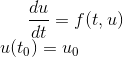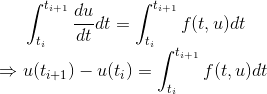本章涉及知识点
1、微分方程的定义
2、一阶线性微分方程的定义
3、求齐次线性方程通解的算法
4、求非齐次线性方程通解的算法
5、伯努利方程的变化算法
6、案例微分方程的分析
7、纯数学算法推导案例的微分方程
8、Euler算法的推导
9、编程实战案例微分方程在不同算法下的计算结果和误差
一、微分方程的定义
在许多实际问题,尤其是金融问题,往往不能直接列出所需要研究的函数的具体表达式,但是根据使用场景,却可以列出待研究的函数与其导数的关系式,而关于函数和其导数的方程就称之为微分方程,那么从这个方程中找出未知函数,就是求解微分方程的解
一般的,在满足初始条件下,微分方程包含未知函数的一阶导数
上述微分方程就叫做一阶微分方程
二、一阶线性微分方程的定义
上述方程是关于未知函数y及其一阶导数的一次方程,我们称之为一阶线性微分方程
方程是齐次的定义为
而方程是非齐次的定义为
求解非齐次微分方程的解,我们需要
(1)、写出对应于非齐次线性方程的齐次线性方程,求出齐次线性方程的通解
(2)、通过常数易变法,求出非齐次线性方程的通解
三、求齐次线性方程通解的算法
对于齐次方程,我们用分离变量法,得到
提出常数C1化简得
四、求非齐次线性方程通解的算法
得到齐次方程的通解后,我们使用常数易变法,将齐次方程通解中的常数C换做未知函数u(x),变化得
我们对y进行求导,得到
将导数带入非齐次线性方程中,得
两端积分得
将求解到的u带入y,就得到了非齐次方程的通解
我们将通解写成两项之和,得到
观察分析上式可以看到,一阶非齐次线性微分方程的通解 = 齐次方程的通解 + 非齐次方程的一个特解
五、伯努利方程的变化算法
从一阶线性微分方程中可以看到,P(x)和Q(x)当只有P(x)是关联未知函数y,我们可以用上述算法求解该方程。但是当Q(x)也关联未知函数y,此时应该如何求解方程呢?
上述方程叫做伯努利方程,显然当n=0或n=1时,就是非齐次线性方程,而当n不等于0和1时,这个方程就不是线性的,为此,我们需要利用上述算法求解该方程,就需要通过变量的代换,将它转化为线性的即可
我们将伯努利方程两端同时除以y^n得
因为
为此我们引入新的因变量z
则z的导数写为
将伯努利方程两端同时乘以(1-n)得
可以看到上式的P(x)与z有关联,而Q(x)已经和z没有了关联,即原方程已经变成了线性方程,我们就可以按照之前的算法求出方程的通解,在用z带回y就可以得到伯努利方程的通解
六、案例微分方程的分析
介绍了非齐次线性方程和伯努利方程求解通解的算法后,我们来求下面方程的通解
分析可知,该方程数非线性方程,属于n=-1的伯努利方程,直接的数学解法需要做伯努利变化为线性方程,再利用非齐次线性方程的解法来求解通解,下面我们先用数学方法来求解
七、纯数学算法推导案例的微分方程
将案例方程两端同时乘以y得
令
带入y得
我们从上式中写出P(x)、Q(x)以及P(x)的积分
带入非齐次线性方程的通解得
下面我们需要单独来求解上式中的积分,使用分部积分法得
将积分的结果带入非齐次线性方程的通解得
将z带回y得
为此我们求出了案例方程的通解,下面带入初始条件y(0)=1得
最终我们得到了案例方程的精确解为
八、Euler算法的推导
上面我们用纯数学知识推导出了案例方程的精确解,但是计算机显然不会分部积分法,我们任然需要从微分方程的原理出发
我们回到微分方程的定义
我们将微分方程在区间[ti,ti+1]上积分得
在区间[ti,ti+1]上将f(t,u)近似的看做常数f(ti,ui),则有
上式称为Euler算法,可以看到这是一个递推式算法,可以由已知初值u0推导至un
而Euler算法的几何意义为:
过点(t0,u0),以f(t0,u0)作为斜率作直线L0,得
求出直线L0在t1=t0+h的值u1,得
得到u1后,再过点(t1,u1),以f(t1,u1)作为斜率作直线L1,得
求出直线L1在t2=t1+h的值u2,得
如此继续迭代下去,可以求出经过
节点列表的一条直线,所以Euler算法也叫做折线法,用n段直线绘制成一条折线,来拟合函数曲线
九、编程实战案例微分方程在不同算法下的计算结果和误差
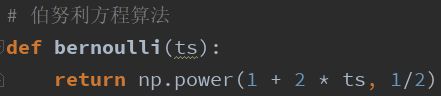
下面我们通过伯纯数学的努利算法和Euler迭代算法来编程比较案例方程的结果值
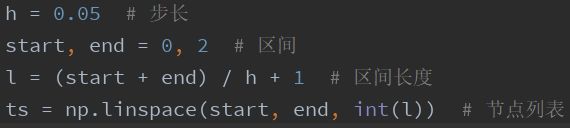
定义区间和步长为
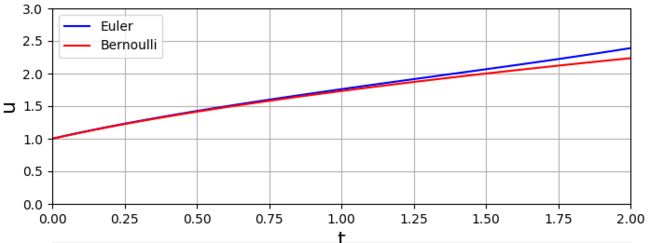
作图画出两种算法的计算结果来直观比较
可以看到当步长h=0.05时,Euler算法的精确度在下降,证明了误差在迭代传播
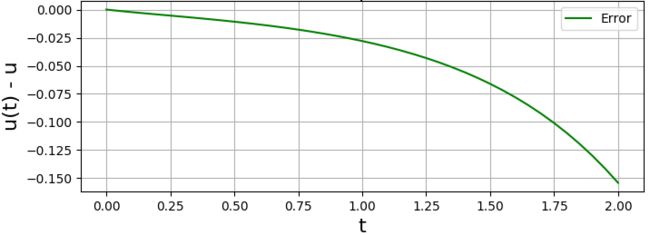
我们用伯努利理论值减去Euler值,画出Euler算法的误差曲线
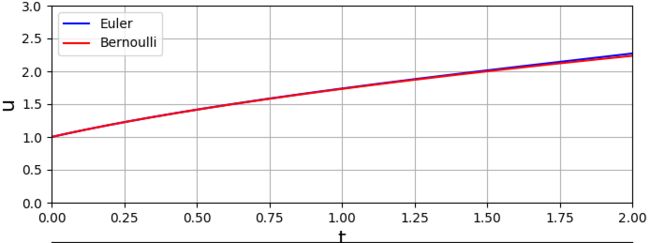
当我们缩小步长h=0.01时,两种算法的计算结果和Euler算法的误差为
可以看到步长的缩小,拟合效果更加出色,误差也在减小
案例代码见:一阶非齐次微分方程的算法