Verilog乘法器

硬件乘法器——由组合逻辑组合的乘法器
一． 整数乘法器：
1.1整数的概念：
整数包括：短整数（short integer）、中整数（integer）和长整数（long integer）

① 短整数的最高位是符号位，符号位的正负表示了该值是“正还是负”，正值的表示方法一般是8位二进制数来表示，负值的表示方法是以补码来表示
+127——8’b0111_1111（表示位宽为8的二进制数）
+4——8’b0000_0010
-4——8’b1111_1100（在原码的基础上先求出反码，再在末位加上1求出补码）
比如求出-4的补码的操作：
8’b0000_0100;表示4
8’b1111_1011求出4的反码
8’b1111_1100这就是补码
② 短整数里面的一个特殊存在8’b1000_0000：
+127——8’b0111_1111
划分——8’b1000_0000
-127——8’b1000_0001（可以这么说：在8’b1000_0000之前的都是正值，在其后的都是负值）
③ 正值可以经过“求反加一成正值”，负值同样可以“负值求反加一成正值”：
-4——8’b1111_1100
求反——8’b0000_0011
加一——8’b0000_0100
1.2乘法器
在传统的概念上乘法等价于：“重复几次”，打个比方：B= 4，A * B亦即A要重复加4次才能得到答案，在乘法中，“负值正值的关系”就是异或的关系

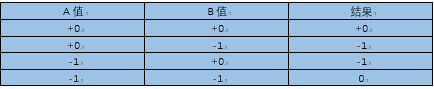
从上面的内容看出：无论A值和B值是什么样的“正值和负值的关系”，结果C都是一样，所以我们可以有一个想法：“在做乘法的时候只是我们只要对正值进行操作，然而‘负值和正值的结果’，我们用异或关系来判断”
实验一：传统的乘法器（代码有点冗长，不是我现在能驾驭的）
该乘法器的大致思路是：
1） 在初始化之际，取乘数和被乘数的正负关系，然后取被乘数和乘数的正值
2） 每一次累加操作，递减一次乘数，直到乘数的值为0，表示操作结束
3） 输出结果根据正负关系取得
先来看一下简单的二位乘法器：（假设A0和B0都代表十位数字、B1和A1分别代表个位数字）A0A1B0B1，可以看见下面的表格：（P0到P3分别代表着得到的数字的各位）

根据表格可以得到：p3=A0A1B0B1
p2=A1&(_A0)&B1&(B0)+A1&(_{A0)&B1&B0+A1&A0&B1&(}B0)+A1&(_{A0)&B1+A1&B1&(}B0)
所以我们可以写出门级的结构描述仿真文件：
①

module multiply#(parameter MSB = 2)
(
	input[MSB-1:0] a,b,
	output[2*MSB-1:0] outcome
);
assign outcome = a*b;
endmodule

下面的是测试文件：

module tb_multiply();
	reg[1:0] Ain,Bin;
	reg clk;//时钟
	wire[3:0] outcome;
	initial
		begin
			#1
			Ain = 2'b00;
			Bin = 2'b00;
			clk = 0;
		end
	always #5 clk = ~clk;
	always @(posedge clk)
		begin
			Ain = {$random} % 4;
			Bin = {$random} % 4;
		end
		multiply m1(Ain,Bin,outcome);
endmodule

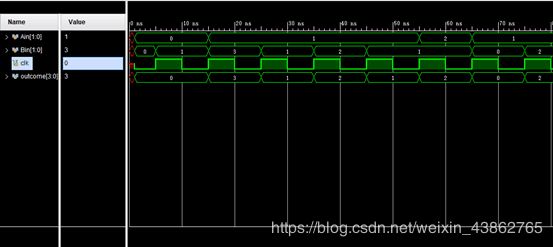
得到的仿真结果图是:

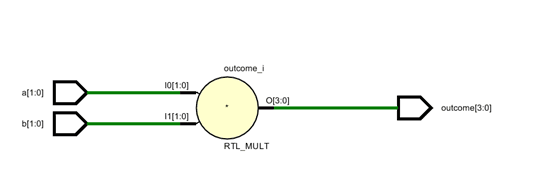
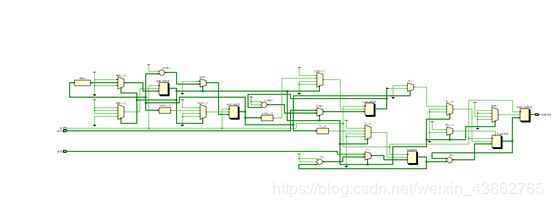
得到的RTL电路图是：

②下面的是串行乘法器：
两个N位二进制数x、y的成绩用简单的方法来计算就是利用移位操作来实现
框图;

状态图是：

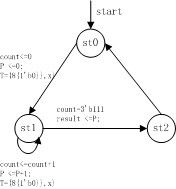
仿真文件的源代码是;

module multiply1(clk, x, y, result);
    input clk;
    input [7:0] x, y;//8位线网型信号x,y
    output [15:0] result;//16位线网型信号result
    reg [15:0] result;
    parameter s0 = 0, s1 = 1, s2 = 2;//这个可以理解成C语言里面的宏定义
    reg [2:0] count = 0;
    reg [1:0] state = 0;//相当于初始化了，开始赋值state = 0，执行case:0语句
    reg [15:0] P, T;
    reg [7:0] y_reg;
    always @(posedge clk) begin
        case (state)//时钟模块边沿触发之后就开始执行,<=也相当于赋值（非阻塞），阻塞和非阻塞的区别就是：阻塞：你不干完不准回来；非阻塞：你先干，我看看还有其他事没有
            s0: begin
                count <= 0;
                P <= 0;
                y_reg <= y;
                T <= {{8{1'b0}}, x};//T的高8位是0，后面的8位是x，拼接运算
                state <= s1;//state被赋值为1.开始执行下一个选择语句
            end
            s1: begin
                if(count == 3'b111)
                    state <= s2;
                else begin
                    if(y_reg[0] == 1'b1)//y_reg最低位是1的话，就会按照顺序向左进位进行求解
                        P <= P + T;
                    else
                        P <= P;
                    y_reg <= y_reg >> 1;
                    T <= T << 1;
                    count <= count + 1;
                    state <= s1;
                end
            end
            s2: begin
                result <= P;
                state <= s0;
            end
            default: ;
        endcase
    end
endmodule

测试代码：

module tb_mutiplier();
reg clk;
reg[7:0] Ain,Bin;
reg[15:0] result;
initial
	begin
		#1
		Ain = 0;
		Bin = 0;
		clk = 0;
		result = 0;
	end
always #5 clk = ~clk;
always @(posedge clk)
	begin
		#1
		Ain = {$random} % 2;
		Bin = {$random} %2;
		#5
		Ain = 8'b0100_0000;
		Bin = 8'b1010_0011;
	end
multiply1 u1(Ain,Bin,result);
endmodule

仿真波形图：

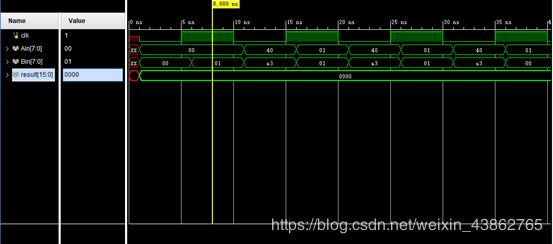
RTL电路图是：

缺点：乘法功能是正确的，但计算一次乘法需要8个周期，因此，可以看出串型乘法器速度比较慢、时延大
优点：该乘法器所占用的资源是所有类型乘法器中最少的，在低速的信号处理中有广泛的使用。
② 流水线乘法器：
一般的快速乘法器通常采用逐位并行的迭代阵列结构，将每个操作数的N位都并行地提交给乘法器，但是一般对于FPGA来讲，进位的速度快于加法的速度，这种阵列并不是最优的。所以可以采用多级流水线的形式，将相邻的两个部分乘积结果再加到最终的输出乘积上，即形成一个二叉树形式的结构，这样对于N位乘法器需要log2(N)级来实现
原理图：

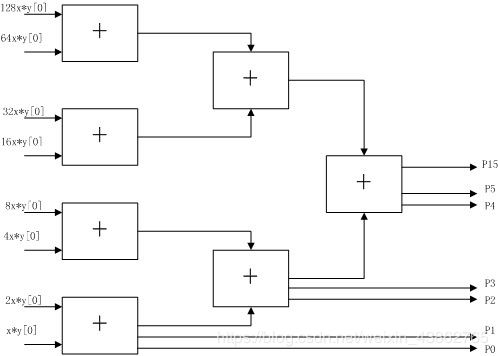
源文件代码：

module multiply2(a,b,clk,rstn,out);
	input [7:0] a,b;//定义a,b是8位
	input clk;//定义时钟模块
	input rstn;//默认是1位
	wire practice = rstn & 1;
	wire s0 =0 ,s1 =1;
	output reg[15:0] out;//a和b都是4位，所以最后的成绩最高是8位
		reg [15:0] stored0,stored1,stored2,stored3,stored4,stored5,stored6,stored7;
		reg [15:0] out1,out2;
		reg [15:0] add1,add2,add3,add4;
	always @(posedge clk or negedge rstn)//当n的下降沿或者是clk的上升沿的时候，就开始执行always下的语句
	case(practice)//如果n是0的情况下，就开始执行下面的语句
		s0:
		begin
			out <= 0;
		    stored0 <= 0;
		    stored1 <= 0;
			stored2 <= 0;
			stored3 <= 0;
			stored4 <= 0;
			stored5 <= 0;
			stored6 <= 0;
			stored7 <= 0;
			add1 <= 0;
			add2 <= 0;
			add3 <= 0;
			add4 <= 0;
		end
		s1://n不是0的情况下，开始下面的语句块
			begin
				stored0 <= b[0]? {8'b0, a} : 16'b0;/*stored开始默认值是0，所以这个语句的意思是：如果b的最低位是0的话，那么stored的值就是{8'b0,a}，并且高8位是0，
				低8位是a的值；否则的话，那么stored的值就是16位0*/			
				stored1 <= b[1]? {7'b0, a, 1'b0} : 16'b0;
				stored2 <= b[2]? {6'b0, a, 2'b0} : 16'b0;
				stored3 <= b[3]? {5'b0, a, 3'b0} : 16'b0;
				stored4 <= b[4]? {4'b0, a, 4'b0} : 16'b0;
				stored5 <= b[5]? {3'b0, a, 5'b0} : 16'b0;
				stored6 <= b[6]? {2'b0, a, 6'b0} : 16'b0;
				stored7 <= b[7]? {1'b0, a, 7'b0} : 16'b0;
				add1 <= stored1 + stored0;
				add2 <= stored3 + stored2;
				add3 <= stored5 + stored4;
				add4 <= stored7 + stored6;
				out1 <= add1 + add2;
				out2 <= add3 + add4;
				out <= out1 + out2;
	   		 end
	   		 default;
	 endcase
endmodule

测试文件代码：

module tb_multiply2();
	reg[7:0] Ain,Bin;
	reg clk,rstn;
	wire [15:0] out;
	initial
		begin
			#1
			Ain = 0;
			Bin = 0;
			clk = 0;
			rstn = 0;
		end
	always #5 clk = ~clk;
	always @(posedge clk or negedge rstn)
		begin
			Ain = {$random}%4;
			Bin = {$random}%4;
		end
	multiply2 u2(.a(Ain),.b(Bin),.clk(clk),.rstn(rstn),.out(out));
endmodule

波形图：

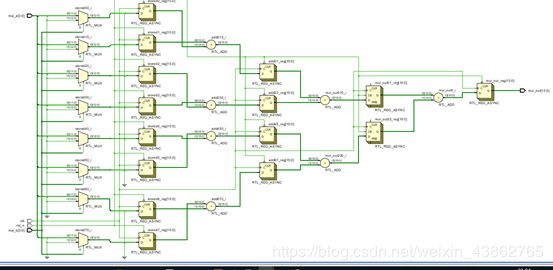
RTL电路图是：

觉得本文可以的同学可以关注一下微信公众号“空谷小莜蓝”，我相信后期微信公众号会越来越好看的，谢谢~~