多示例多标签学习（MIML系列文章总结）

从入学以来就一直调研图像标注相关文章。调研发现，传统的监督学习中，一个图像区域以一个instance（示例）呈现，并仅关联于一个label（标签）。很多图像多标签标注的方法是通过将图像进行物体分割（object segmentation）或物体检测（object detection），然后对每个区域的物体进行标注。而多示例多标签学习（MIML）方法省去了检测/分割部分工作。

MIML的问题阐述。给定一个MIML数据集由{(X1, Y1), (X2, Y2), …, (Xn, Yn)}表示，其中有n幅图像，即n个bags（包），每个bag Xi由z个instance组成即{xi,1, xi,2, …, xi,z}；每幅图像的对应标签集合由L个标注组成{y1, y2, …, yL}。
下面我将从三篇文章对MIML的算法思想进行解读。

Fast Multi-Instance Multi-Label Learning

Problem Defination

处理多标签分类的最简单的方法是利用训练多个单标签分类模型将其分解成多个单标签问题。然而传统的这种方法将标签进行独立处理忽略了标签之间的关联关系。本文将多标签多示例学习分解为了两个部分：第一个部分将原始的图像特征空间进行线性映射到一个低维的共享空间；然后第二部分基于这个共享空间学习标签特定模型。
给定一个示例x，定义如下的分类模型： $f_l(x)=w_l^T{W}_{0}x$
其中，$W_0$代表将特征空间$x$映射到共享空间的转换矩阵，$w_l$代表是标签$l$的权重向量，如图3所示。

此文又提出了利用sub-concept（子概念）的方法来处理复杂文中提到，即使图4所示的三幅图像都具有标签mountain，然而其却具有不同的子概念：即a mountain of sand, a snow mountain, mountain covered with trees。此处，假设每个标签具有$K$个子概念，对于具有标签$l$的给定示例，通过检查$K$个模型的预测值，然后选择具有最大预测值的子概念所在的标签作为其预测标签$l_i$，公式如下
$f_l(x)=ma{x}_{k=1...K}(f_{l,k(x)})=ma{x}_{k=1...K}(w_l^T{W}_{0}x$)

objective:

通过这样的方式，将MIML分类问题转换为了标签排序（label ranking）问题，因此，训练目标是将相关标签排序在非相关标签前面。
定义得分函数$R(x,l)=\sum I[f_j(X)>f_i(X)]$，通过这个函数计算不相关标签在包$X$中排在相关标签前面的个数。基于$R$，进一步定义ranking error $e(X,l)={\sum }_{i=1}^{R(X,l)}1/i$，显然如果排序错误越大那么得分$R$就会越高。将此得分扩展至所有训练标签集$Y$中，其表示为
$\Psi (X,l)={\sum }_{j\in Y}e(X,l)$
那么，最后的训练目标函数就是最小化排序损失，如下：

DeepMIML

特点是用深度神经网络模型进行多示例多标签学习。利用deep neural network来提取示例特征，并完成示例和标签的匹配打分。

Approach

单个示例的2D子概念层（2D sub-concept layer for single instance）

在语义丰富的任务中，类别标签可能带有复杂的信息，因此，这篇文章延续了上一篇提出的示例子概念的思想，通过构建sub-concept layer完成每个类别标签在instance和sub-concept之间的匹配打分。具体来说，一个示例特征用$x$表示，一个全连接2D层的大小为$K\ast L$。对于一个给定的示例向量$x$，这个子概念层中的$(i,j)$结点代表这个示例向量$x$与第$j$个标签的第$i$个子概念的得分。那么，子概念层中第$(i,j)$个结点的激励函数为$c_{i,j}=f(w_{i,j}x+b_{i,j})$
此处，$f(\cdot )$是激励函数，权重项链$w_{i,j}$可以被翻译为第$j$个标签的第$i$个子概念与特征向量匹配模板。
为了预测label，利用column-wise pooling操作在$K\ast L$大小的子概念层，最后得到$L\ast 1$大小的label的分层，意味着示例$x$与输出标签的匹配得分，这部分操作如图5所示。

多个示例的3D子概念层（3D sub-concept layer for multiple instances）

我们都知道，在多示例多标注学习中，一幅图像被视为装有多个instacne的一个bag，因此，本文提出了3D子概念层用于建模图像特征、多个子概念和多个示例的匹配得分。理解了2D子概念层，3D子概念层就很清晰了。即把多个2D子概念层进行堆叠，其深度为示例的数量即标签的数量。3D子概念层中第$（i,j,k）$个结点的意义代表着第$k$个示例特征与第$j$个标签的第$i$个子概念的匹配得分。
为了得到示例和标签的关系，进行两次池化操作。具体来说，第一次在3Dtensor上进行垂直最大池化，得到大小为$L\ast M$ 的2D得分层，在这层中，位于$(i,j)$ 的结点代表着instance $i$ 和label $j$的得分。第二次池化操作后得到大小为$L\ast 1$的标签得分层。

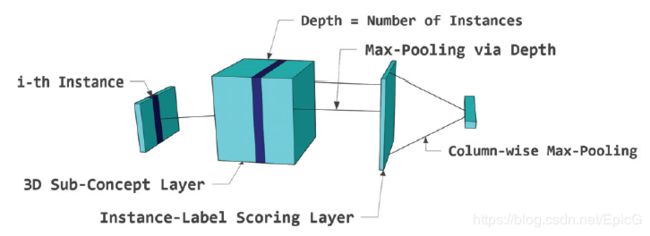
DeepMIML

传统的利用深度神经网络提取图像的特征是从CNN的全连接层(FC7)提取的，然而这样的方法把图像特征编码为了整体特征，不能很好的体现instance level的特征。因此，本文提出直接提取conv层得到的三维特征向量（如1414512），这样，每一个14*14的向量（一共有512个）可以被看做输入图像的一个示例特征。通过提取conv层的特征直接得到the representation of instances in one bag。
因此在整个DeepMIML网络中，有一个基于VGG-16构建的instance generator即上段提到的示例特征生成网络，一个经过池化得到的Deep instance层，一个3D子概念层，一个经过池化得到的示例得分层。

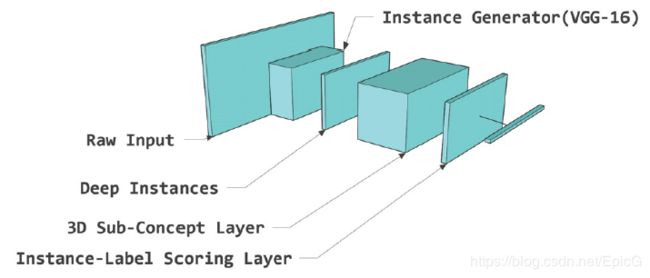
A Deep Multi-Modal CNN for Multi-Instance Multi-Label Image Classification

这篇文章在MIML上的特点是利用了多模态信息，并且考虑了标签间的信息。
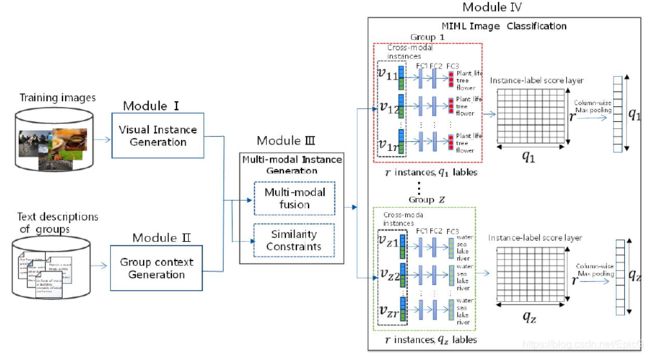
我们根据这个算法流程来讲解一下这个网络架构。首先，将类别标签分为$z$组，每一组包含$r$个多模态示例和$q_i$个标签。MMCNN-MIML以一幅图像$I$和每组的文本描述为输入。具体来说，$I^m$输入模块一然后产生一袋视觉示例，即$X_i^m=Visua{l}_{I}nstanc{e}_{G}eneration(\theta ,I^m)$；其次，第$i$组的文本描述输入模块二产生一组语境表现特征$t_i$（context representation）,即$t_i=Grou{p}_{C}ontex{t}_{G}eneration(T_i)$；在模块三中，生成的视觉示例平均分至每个预先分好的组中，之后通过拼接视觉示例特征和语境表现特征得到多模态示例$V_i^m$，即$V_i^m=Multimoda{l}_{I}nstanc{e}_{G}eneration(t_i,X_i^m)$；最后在模块四中国，输出第$i$个组的每一个标签的预测分布$p_i^m$，即$p_i^m=MIM{L}_{i}mag{e}_{c}lassification(V_i^m)$。

下面，分别介绍每个模块的具体情况。

Module I：Visual Instance Generation（VIG）

文中提到，利用现有的CNN网络并不能很好的进行多标签图像分类，其原因主要为两点：第一，现有的多标签数据集的训练数据的量不足以很好地拟合端到端的CNN；第二，以往的CNN将每幅输入图像作为一个示例，并通过全连接层将输入图像编码为一个密集的一维向量。这样的方式难以区分每个示例的representation。
为了解决第一个问题，本文提出利用在ImageNet上预训练好的CNN模型中的一部分，之后在实验数据集上进行微调（基本都会这样做，不细讲）。具体的网络结构安排为，将VGG16网络的后三个卷积层和相应的池化层及最后的全连接层替换为两个adaptation layers（结构如图8所示）。
为了解决第二个问题，本文和DeepMIML一样，选择使用卷积层而不是全连接层的特征表示，原因为不同的filter会被不同的语义内容激励，所以说用卷积层产生的特征图能更好的代表instance的特征表示。具体来说，最后一个adaptation layer生成大小为$d\ast 14\ast 14$的特征集，每一个维度为$14\ast 14$的特征图作为一个视觉示例$x_{ij}^m$的特征表示。然后将这些生成的视觉示例分至每个标签组，这样$d$的值即为$z\ast r$（一共有$z$组，且每个标签组中含有$r$个视觉示例）。

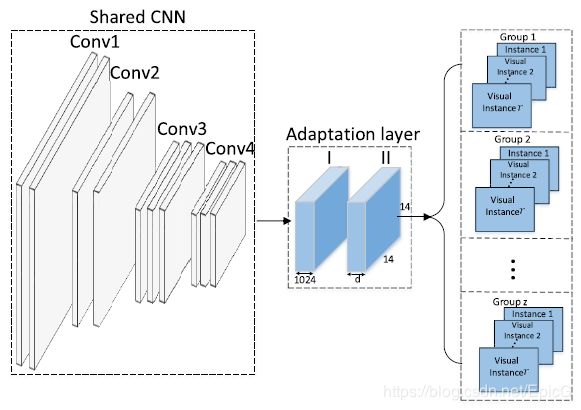
Module II: Group Context Generation

本文的一个特色就是借助多模态数据拟补单模态图像数据的数量不足的缺点。其采用的做法是结合每一组的文本描述来为相关的视觉示例提供语境信息，而不是传统的利用图像描述。在这个模块中，每组描述首先被编码至固定长度的向量，然后通过MLP（多层感知机）映射到与视觉示例相同维度的向量表示。具体做法如图9，即文本利用skip-thought模型进行编码，然后通过多层感知机得到最终的向量表示。

Module III: Muti-Modal Instance Generation

此部分主要讲解了，怎样将文本描述的向量表示与视觉示例的向量表示进行融合得到多模态示例的向量表示。此操作的对象主要是每个组，因此，在组内本文引入了相似度页数使得视觉示例与相应的语境表示距离相近。
在上述分好的每个组中，通过拼接视觉示例和相应的语境表示生成多模态示例。这种做法的主要原因是不同模态包含了不同的信息，可以拟补其他模态信息的不足（参见多模态学习→ _→）具体的做法是，对于第$i$组，第$j$个示例的多模态信息由$v_{ij}^m$表示，通过拼接视觉示例$x_{ij}^m$和语境表示$t_i$，其中$||$表示拼接操作符，$\alpha$是一个权重调节参数。公式为$v_{ij}^m=\alpha \cdot x_{ij}^m||(1-\alpha )\cdot t_i$ 。
并且，由于一个组中的视觉示例的特征表示与这个组的语境表示应具有更高的语义相似度（比其他组的语境表示），因此定义相似度约束：
$Hing{e}_{l}oss(X_i^m,T_i)={\sum }_{u̸=i,u=1}^{z}max[0;margin-cos(t_i,w_i)+cos(t_u,w_i)]$

Module IV: MIML Image Classification

在此模块中，对于每个图像，我们首先在每个组中的实例级别上执行标签预测，然后我们在整个图像的包级别上进行最终预测。如图10所示。具体来说，每个组通过三个全连接层得到最终的标签预测，即FC1，FC2，FC3。其作用是对每一个示例生成一些相关标签。在第$i$组中，FC3层使用sigmoid作为激活函数来产生示例级预测，即每个示例与该组标签之间的匹配分数。因此，我们可以获得$r\ast q_i$大小的2D示例-标签得分层。
最后，为了进行包级别的预测，我们在示例标签平分层上进行逐列最大池化操作以产生大小为$q_i$的向量，其中每个条目表示图像与每个组的一个标签之间的匹配分数，最后通过连接所有组的得分预测来获得包级别的得分预测。每组的损失函数定义如下
$-{\lambda }_1\cdot {\sum }_{k=1}^{q_i}[y_k^m\cdot log(p_k^m)]+{\lambda }_2\cdot Hing{e}_{l}oss(X_i^m,T_i)$
其中，$p_k^m$是这个组中图像$I^m$与第$k$个标签的预测得分，$y_k^m$为$I^m$的真实标签。$\lambda$为参数。

---------------------------------------------------------------------------------完结-----------------------------------------------------------------------------------------
真的要写吐了。。