学习笔记：序列分类问题详解

在上一篇文章中，主要介绍了RNN的几种结构，并且介绍了如何利用Char RNN进行文本生成。Char RNN对应着N VS N的RNN结构。在这篇文章中，将专注于另一种RNN结构；N VS 1。这种结构的输入为序列，输出为类别，因此可以解决序列分类问题。常见的序列分类问题有文本分类、时间序列分类、音频分类等等。这篇文章会使用TensorFlow制作一个简单的两类序列分类器

1 N VS 1的RNN结构

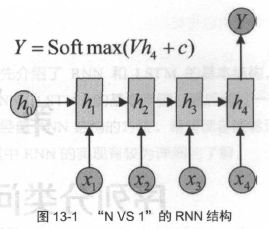
先来简单地复习N VS 1的RNN结构，如图13-1所示。

x1,x2,...,xT x 1 , x 2 , . . . , x T 为输入放入数据，Y为最终的分类。在不同的问题中，输入护具x有不同的含义，如：

• 对于文本分类，每一个 xt x t 是一个词的向量表示。
• 对于音频分类，每一个 xt x t 是一帧采样的数据。
• 对于视频分类，每一个 xt x t 是一帧图像（或从单帧图像中提取的特征）

这种N VS 1的RNN结构用公式来表达是
ht=f(Uxt+Wht−1+b) h t = f ( U x t + W h t − 1 + b )
Y=Softmax(VhT+c) Y = S o f t m a x ( V h T + c )
每次只对最后一个隐层状态 hT h T 计算类别。请注意，通常输入的序列长度都是不等长的。此时， hT h T 取对应的长度。如一个长度为3的句子，对 h3 h 3 进行计算，一个长度为5的句子，对 h5 h 5 进行计算。

2 序列分类问题与数据生成

这篇文章中，会处理一个最简单的序列分类问题：数值序列分类，即数列的分类。假设现在有两类数列，它们分别是：

• 线性数列：如(1,2,3,4,5,…),(0,5,10,15,20,…)等
• 随机数列：如(5,1,6,2,10…),(8,3,1,9,7…)这种完全没有规律的数列。

希望能训练一个RNN分类器，将这两类数列自动分开。有一点要注意的是，这里数列的长度是不固定，但它们有一个共同的最大序列长度，这也和通常要处理的问题类似。

很显然，这种数列分类问题是向量序列分类的最简单的形式。它相当于在第1节的公式中，每一个 xt x t 都取一个数字（而不是向量）。在使用TensorFlow搭建RNN模型之前，先创建下面的类，用于生产数列数据：

# coding: utf-8
from __future__ import print_function

import tensorflow as tf
import random
import numpy as np

# 这个类用于产生序列样本
class ToySequenceData(object):
    """ 生成序列数据。每个数量可能具有不同的长度。
    一共生成下面两类数据
    - 类别 0: 线性序列 (如 [0, 1, 2, 3,...])
    - 类别 1: 完全随机的序列 (i.e. [1, 3, 10, 7,...])
    注意:
    max_seq_len是最大的序列长度。对于长度小于这个数值的序列，我们将会补0。
    在送入RNN计算时，会借助sequence_length这个属性来进行相应长度的计算。
    """
    def __init__(self, n_samples=1000, max_seq_len=20, min_seq_len=3,
                 max_value=1000):
        self.data = []
        self.labels = []
        self.seqlen = []
        for i in range(n_samples):
            # 序列的长度是随机的，在min_seq_len和max_seq_len之间。
            len = random.randint(min_seq_len, max_seq_len)
            # self.seqlen用于存储所有的序列。
            self.seqlen.append(len)
            # 以50%的概率，随机添加一个线性或随机的训练
            if random.random() < .5:
                # 生成一个线性序列
                rand_start = random.randint(0, max_value - len)
                s = [[float(i)/max_value] for i in
                     range(rand_start, rand_start + len)]
                # 长度不足max_seq_len的需要补0
                s += [[0.] for i in range(max_seq_len - len)]
                self.data.append(s)
                # 线性序列的label是[1, 0]（因为我们一共只有两类）
                self.labels.append([1., 0.])
            else:
                # 生成一个随机序列
                s = [[float(random.randint(0, max_value))/max_value]
                     for i in range(len)]
                # 长度不足max_seq_len的需要补0
                s += [[0.] for i in range(max_seq_len - len)]
                self.data.append(s)
                self.labels.append([0., 1.])
        self.batch_id = 0

    def next(self, batch_size):
        """
        生成batch_size的样本。
        如果使用完了所有样本，会重新从头开始。
        """
        if self.batch_id == len(self.data):
            self.batch_id = 0
        batch_data = (self.data[self.batch_id:min(self.batch_id +
                                                  batch_size, len(self.data))])
        batch_labels = (self.labels[self.batch_id:min(self.batch_id +
                                                  batch_size, len(self.data))])
        batch_seqlen = (self.seqlen[self.batch_id:min(self.batch_id +
                                                  batch_size, len(self.data))])
        self.batch_id = min(self.batch_id + batch_size, len(self.data))
        return batch_data, batch_labels, batch_seqlen

构造函数中参数的含义为：

• n_samples：数据集中的总样本数。
• max_seq_len：数列的最大长度。
• min_seq_len：数列的最小长度。
• max_value：数列中数的最大值。

这几个参数的含义应该不难理解。唯一需要注意的是此时数列长度是不一致的，最小的长度为min_seq_len，最大的长度为max_seq_len。不过，为了方便对数据整体进行处理，在长度不足max_seq_len 的数列末尾补0，将其长度变为max_seq_Ien，并用self.seq_len记录它的真正长度。

每次调用next方法，都会得到三个变量batch_data、batch_labels 、batch_seqlen，它们分别表示数列数据、数列的标签、数列的真正长度。我们可以借助下面的实验程序理解这几个变量的含义：

# 这一部分只是测试一下如何使用上面定义的ToySequenceData
tmp = ToySequenceData()

# 生成样本
batch_data, batch_labels, batch_seqlen = tmp.next(32)

# batch_data是序列数据，它是一个嵌套的list，形状为(batch_size, max_seq_len, 1)
print(np.array(batch_data).shape)  # (32, 20, 1)

# 我们之前调用tmp.next(32)，因此一共有32个序列
# 我们可以打出第一个序列
print(batch_data[0])

# batch_labels是label，它也是一个嵌套的list，形状为(batch_size, 2)
# (batch_size, 2)中的“2”表示为两类分类
print(np.array(batch_labels).shape)  # (32, 2)

# 我们可以打出第一个序列的label
print(batch_labels[0])

# batch_seqlen一个长度为batch_size的list，表示每个序列的实际长度
print(np.array(batch_seqlen).shape)  # (32,)

# 我们可以打出第一个序列的长度
print(batch_seqlen[0])

3 在TensorFlow中定义RNN分类模型

3.1 定义模型前的准备工作

在正式定义模型前，要做一些准备工作，如给出运行时的一些参数，创建数据集，创建模型中可能用到的变量等，相应的程序如下：

# 运行的参数
learning_rate = 0.01
training_iters = 1000000
batch_size = 128
display_step = 10

# 网络定义时的参数
seq_max_len = 20 # 最大的序列长度
n_hidden = 64 # 隐层的size
n_classes = 2 # 类别数

trainset = ToySequenceData(n_samples=1000, max_seq_len=seq_max_len)
testset = ToySequenceData(n_samples=500, max_seq_len=seq_max_len)

# x为输入，y为输出
# None的位置实际为batch_size
x = tf.placeholder("float", [None, seq_max_len, 1])
y = tf.placeholder("float", [None, n_classes])
# 这个placeholder存储了输入的x中，每个序列的实际长度
seqlen = tf.placeholder(tf.int32, [None])

# weights和bias在输出时会用到
weights = {
    'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
    'out': tf.Variable(tf.random_normal([n_classes]))
}

定义的参数含义为：

• learning_rate：学习率。
• training_iters：最大运行的步数。这里定义的最大步数为1000000，定义成更大的步数可以获得更高的准确率，我们在运行这个程序时可以自行尝试。
• batch size：每个batch中的序列数。
• display_step：每隔多少步在屏幕上打出信息。
• seq_max_len：该参数上面解释过，是序列的最大长度。在定义数据集对象以及定义网络时该参数都会被用到。
• nhidden：指RNN的隐层维度大小。
• n_classes：总类别数。

定义了3个占位符，这些占位符用于向模型提供输入输出数据：

• x：输入的数列数据。这些占位符和在第2节中的变量“batch_data”相对应。它的形状为（batch_size，max_seq_len，1）。
• y：输入数列的长度。战歌占位符和在第2节中的变量“batch_labels”相对应。它的形状为（batch_size，）。它的形状为（batch_size，nclasses）。
• seqlen：输入数列的长度。这个占位符和在第2节中的变量“batch_seqlen ”相对应。它的形状为(batch_size, ） 。

此外，还定义了两个变量weights和biases，这两个变量会在后面走义模型时用到（用3.2节） 。

3.2 定义RNN分类模型

有了上面的准备工作后，接下来才是真正的重头戏， 即定义模型的部分：

def dynamicRNN(x, seqlen, weights, biases):

    # 输入x的形状： (batch_size, max_seq_len, n_input)
    # 输入seqlen的形状：(batch_size, )


    # 定义一个lstm_cell，隐层的大小为n_hidden（之前的参数）
    lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden)

    # 使用tf.nn.dynamic_rnn展开时间维度
    # 此外sequence_length=seqlen也很重要，它告诉TensorFlow每一个序列应该运行多少步
    outputs, states = tf.nn.dynamic_rnn(lstm_cell, x, dtype=tf.float32,
                                sequence_length=seqlen)

    # outputs的形状为(batch_size, max_seq_len, n_hidden)
    # 如果有疑问可以参考上一章内容

    # 我们希望的是取出与序列长度相对应的输出。如一个序列长度为10，我们就应该取出第10个输出
    # 但是TensorFlow不支持直接对outputs进行索引，因此我们用下面的方法来做：

    batch_size = tf.shape(outputs)[0]
    # 得到每一个序列真正的index
    index = tf.range(0, batch_size) * seq_max_len + (seqlen - 1)
    outputs = tf.gather(tf.reshape(outputs, [-1, n_hidden]), index)

    # 给最后的输出
    return tf.matmul(outputs, weights['out']) + biases['out']

先熟悉输入的序列数据x，它的形状为(batch_size, max_seq_len, n_input)接着定义了一个BasicLSTMCell，然后使用tf.nn.dynamic_rnn运行这个cell，这相当于调用了max_seq_len次该cell的call函数，得到的outputs的形状为(batch_size, max_seq_len, n_hidden)。这里的走义cell、使用tf.nn.dynamic_rnn都是标准做法，在上篇文章中已经详细地讲解过了， 此处不再展开描述。唯一与之前不同的是，多传入了一个参数sequence_length=seqlen 。

为什么要使用sequence_length参数？原因在于序列是不等长的，每一个batch中，各个序列的长度都记录在seqIen中。在调用tf.nn.dynamic_rnn时
加入参数sequence_length=seqlen, TensorFlow会知道每个序列的具体长度，在RNN执行到对应长度后不再进行运行， 可以节省运行时间。

此外，对于输出outputs的处理也相之前不同。此时定义的是N vs 1的RNN结构，因此必须要获得每个序列对应位置的输出值。如对于长度为10的数列，应该使用第10个隐层的输出计算分类概率。这应该怎么操作呢？由于在TensorFlow中，不能直接使用seqlen取出对应位置的outputs，因此又多定义了一个index变量，借助它和tf.gather函数来实现取出对应位置输出值的功能。

最后，使用之前定义的weights和bais对输出值做一次变换，得到了分类使用的logits，它的形状为（ batch_size, 2），它是该函数的返回值。

3.3 定义损失并进行训练

得到logits后，可以利用它和标签y直接定义损失并训练了，此处的代码比较简单：

# 这里的pred是logits而不是概率
pred = dynamicRNN(x, seqlen, weights, biases)

# 因为pred是logits，因此用tf.nn.softmax_cross_entropy_with_logits来定义损失
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)

# 分类准确率
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

# 初始化
init = tf.global_variables_initializer()

# 训练
with tf.Session() as sess:
    sess.run(init)
    step = 1
    while step * batch_size < training_iters:
        batch_x, batch_y, batch_seqlen = trainset.next(batch_size)
        # 每run一次就会更新一次参数
        sess.run(optimizer, feed_dict={x: batch_x, y: batch_y,
                                       seqlen: batch_seqlen})
        if step % display_step == 0:
            # 在这个batch内计算准确度
            acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y,
                                                seqlen: batch_seqlen})
            # 在这个batch内计算损失
            loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y,
                                             seqlen: batch_seqlen})
            print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
                  "{:.6f}".format(loss) + ", Training Accuracy= " + \
                  "{:.5f}".format(acc))
        step += 1
    print("Optimization Finished!")

    # 最终，我们在测试集上计算一次准确度
    test_data = testset.data
    test_label = testset.labels
    test_seqlen = testset.seqlen
    print("Testing Accuracy:", \
        sess.run(accuracy, feed_dict={x: test_data, y: test_label,
                                      seqlen: test_seqlen}))

一共会训练training_iters次，它的默认值为100 万。训练完成后会在测试集上测试分类的准确率。一般来说，训练100万次后，得到的准确率在90%~ 95%。我们在实验时可以将该训练次数调整得更高，如500万次， 一般都可以得到大于99%准确率的模型。

4 模型的推广

已经使用TensorFlow实现了一个最简单的序列分类：

• 输入的序列的每一步只是一个数。
• 输出只有两类。
• 一般来讲，在处理实际问题时，常常会碰到更复杂的情况，如：
• 输入序列的每一步是一个向量。如在文本分类问题中，输入序列的每一步是单词对应的向量，在视频分类问题中，输入的每一步是单帧图片对应的向量。
• 输出不只有两类。

如何修改上面的代码让它可以处理更复杂的情况呢？首先来看输出有多类时应该怎么处理。之前表示两类时，一类的标签为[0,1]，另一类的标签为[0,0,1]，这实际上是类别的独热表示。因此，当类别数为3时，对应的标签应该是[0, 0, 1], [0, 1, 0] , [0, 0, 1]，以此可以类推到更多的类别。另外，还需要更改参数n_classes，输出时使用的变量weights和bias的形状也会发生变化，最后的输出是对应的类别数了。

如果输入序列的一步是一个向量，应该怎么处理呢？实际上，上面的batch_data以及x的形状为（batch_s ize, max_seq_len, 1），只需要其形状改为（batch_ size, max_seq_len, input_size）可以了，真中每个序列每一步的值是一个长度input_size的向量。

5 总结

在上篇文章的基础上，这篇文章进一步介绍了N VS 1 RNN结构，并介绍了如何利用它处理序列分类问题。使用TensorFlow建立RNN模型，解决了一个最基本的序列分类问题。最后，讨论了如何再把该程序用于更复杂的情形。