莫烦Tensorflow教程（15~22）

十五、卷积神经网络

图像和语言方面结果突出

神经网络是由多层级联组成的，每层中包含很多神经元

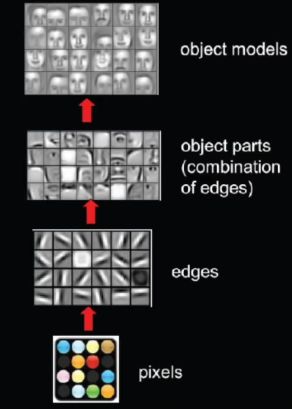
卷积：神经网络不再是对每个像素做处理，而是对一小块区域的处理，这种做法加强了图像信息的连续性，使得神经网络看到的是一个图像，而非一个点，同时也加深了神经网络对图像的理解，卷积神经网络有一个批量过滤器，通过重复的收集图像的信息，每次收集的信息都是小块像素区域的信息，将信息整理，先得到边缘信息，再用边缘信息总结从更高层的信息结构，得到部分轮廓信息，最后得到完整的图像信息特征，最后将特征输入全连接层进行分类，得到分类结果。

详细介绍：

猫的图像，有长、宽、高（颜色信息，黑白高度为1，彩色高度为3）

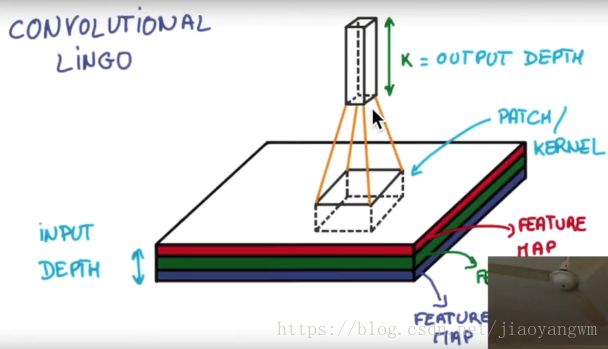
卷积：

经过卷积以后，变为高度更高，长和宽更小的图像，进行多次卷积，就会获得深层特征

1）256*256的输入（RGB为图像深度）

2）不断的利用卷积提取特征，压缩长和宽，增大深度，也就是深层信息越多。

3）分类

池化：

提高鲁棒性

综合结构：

Tensorflow实现

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist=input_data.read_data_sets('MNIST_data',one_hot=True)

def compute_accuracy(v_xs,v_ys):
    #全局变量
    global prediction
    #生成预测值，也就是概率，即每个数字的概率
    y_pre=sess.run(prediction,feed_dict={xs:v_xs,keep_prob:1})
    #对比预测的数据是否和真实值相等，对比位置是否相等，相等就对了
    correct_prediction=tf.equal(tf.arg_max(y_pre,1),tf.arg_max(v_ys,1))
    #计算多少个对，多少个错
    #tf.cast(x,dtype)，将x数据转换为dtype类型
    accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
    result=sess.run(accuracy,feed_dict={xs:v_xs,ys:v_ys,keep_prob:1})
    return result

def weight_variable(shape):
    initial=tf.truncated_normal(shape,stddev=0.1)
    return tf.Variable(initial)

def bias_variable(shape):
    initial=tf.constant(0.1,shape=shape)
    return tf.Variable(initial)

def conv2d(x,W):
    #stride[1,x_movement,y_movement,1]
    return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME') #x,y跨度都为1
def max_pooling_2x2(x):
    return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

# define placeholder for input network
keep_prob=tf.placeholder(tf.float32)
xs=tf.placeholder(tf.float32,[None,784])
ys=tf.placeholder(tf.float32,[None,10])
#-1:代表图像数量不确定,1:黑白色，channel为1
# 将xs变为[28*28*1]的形状
x_image=tf.reshape(xs,[-1,28,28,1])

# conv1 layer
#patch/kernel=[5,5],input size=1也就是图像的深度为1,output size=32也就是卷积核的个数
W_con1=weight_variable([5,5,1,32])
b_conv1=bias_variable([32])
#hidded layer
h_conv1=tf.nn.relu(conv2d(x_image,W_con1)+b_conv1) #output size = 28*28*32
#pooling layer
h_pool1=max_pooling_2x2(h_conv1)                   #output size=14*14*32

# conv2 layer
W_conv2=weight_variable([5,5,32,64])               #patch 5x5,in size 32,out size 64
b_conv2=bias_variable([64])
h_conv2=tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2)#outputsize=14*14*64
h_pool2=max_pooling_2x2(h_conv2)                   #output size=7*7*64

# func1 layer
W_fc1=weight_variable([7*7*64,1024])
b_fc1=bias_variable([1024])

h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64,])    #[n_samples,7,7,64]->[n_samples,7*7*64]
h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1)
h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob)


# func2 layer
W_fc2=weight_variable([1024,10])
b_fc2=bias_variable([10])
prediction=tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2)


#the error between prediction and real data
cross_entropy=tf.reduce_mean(-tf.reduce_sum(ys*tf.log(prediction),reduction_indices=[1]))
train_step=tf.train.AdadeltaOptimizer(0.0001).minimize(cross_entropy)

init=tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        batch_xs,batch_ys=mnist.train.next_batch(100)
        sess.run(train_step,feed_dict={xs:batch_xs,ys:batch_ys,keep_prob:0.5})
        if i%50 ==0:
            print(compute_accuracy(mnist.test.images,mnist.test.labels))

结果：

0.103
0.7985
0.8934
0.9172
0.9296
0.9409
0.9411
0.951
0.9495
0.9536
0.9611
0.9586
0.9643

随机梯度下降训练：

使用一小部分的随机数据来进行训练被称为随机训练（stochastic training）- 在这里更确切的说是随机梯度下降训练。在理想情况下，我们希望用我们所有的数据来进行每一步的训练，因为这能给我们更好的训练结果，但显然这需要很大的计算开销。所以，每一次训练我们可以使用不同的数据子集，这样做既可以减少计算开销，又可以最大化地学习到数据集的总体特性。

十六、Saver 保存读取

Tensorflow目前只能保存Varibales，而不能保存框架，所以需要重新定义一下框架，再把Varibales放进来重新学习。

import tensorflow as tf
import numpy as np
# #save to file
# W=tf.Variable([[1,2,3],[3,4,5]],dtype=tf.float32,name='weight')#2行3列的weight
# b=tf.Variable([[1,2,3]],dtype=tf.float32,name='biases')        #1行3列
#
# init=tf.global_variables_initializer()
#
# #saver用来存储各种变量
# saver=tf.train.Saver()
#
# with tf.Session() as sess:
#     sess.run(init)
#     # 把返回的值保存在save_path中,将sess中的所有东西都保存
#     save_path=saver.save(sess,"my_net/save_net.ckpt")
#     print("Save to path:",save_path)


#restore variables
#只是一个空的框架，把上面保存的东西restore到这个框架中来
W=tf.Variable(np.arange(6).reshape((2,3)),dtype=tf.float32,name="weight")
b=tf.Variable(np.arange(3).reshape((1,3)),dtype=tf.float32,name="biases")

# no need to init step
saver=tf.train.Saver()

with tf.Session() as sess:
    saver.restore(sess,"my_net/save_net.ckpt")
    print("weight:",sess.run(W))
    print("biases:",sess.run(b))

结果：

weight: [[ 1.  2.  3.]
 [ 3.  4.  5.]]
biases: [[ 1.  2.  3.]]

十七、RNN

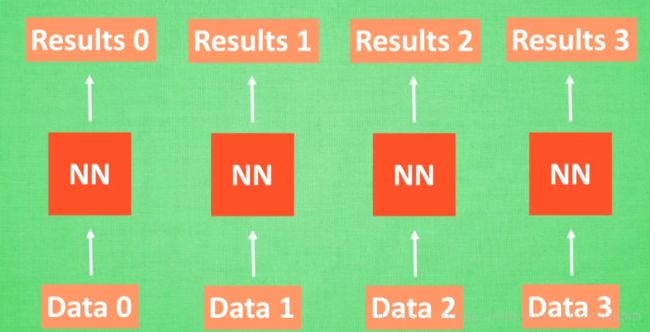
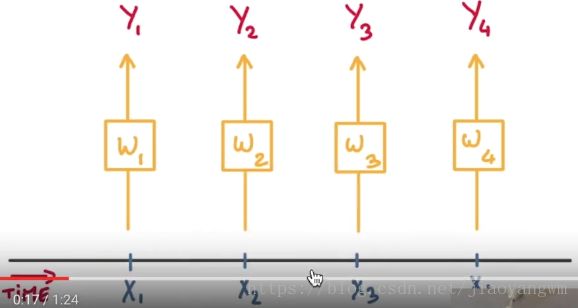
预测的顺序排列是很重要的

序列数据，预测result0的时候是基于Data0，如果数据是有顺序的，那么NN也可以分析出来数据中的关联，就会产生很好的效果。

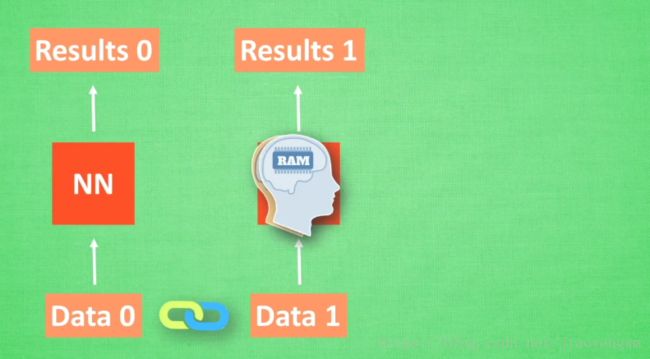
如果让NN了解数据的关联？——记住之前发生的事情

计算Data0之后，把分析结果存入记忆，分析Data1的时候，NN会产生新的记忆，但是两个记忆没有关联，此时就可以将Data0的记忆调用过来，NN会将之前的记忆都累积起来，继续分析则继续累积。

数学分析：

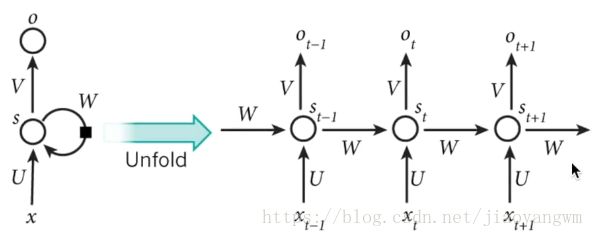
RNN每次运行完之后都会产生一个对于当前的分析(state) S(t) S ( t )

分析 X(t+1) X ( t + 1 ) 时刻，会产生一个 S(t+1) S ( t + 1 ) ， Y(t+1) Y ( t + 1 ) 是由 S(t) S ( t ) 和 S(t+1) S ( t + 1 ) 共同创造的。

RNN的形式：

RNN形式很多变，所以功能越来越强大
原理介绍：

RNN对于处理有序的数据很有效，预测序列化的数据

RNN：

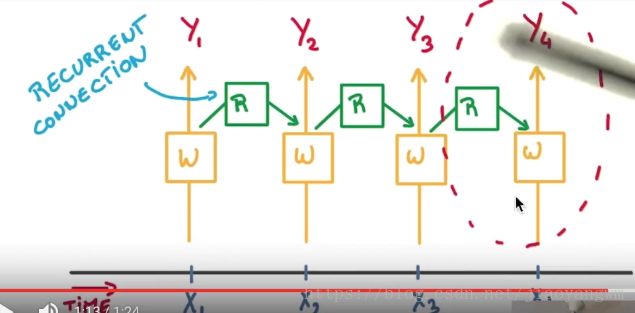
预测有序的数据时，用x1预测得到y1，这部分的内存保存在cell中，之后对输入x2再用这个cell预测y2，在预测时，首先这个cell会调用之前存储的记忆，这部分记忆加上新的输入x2，进行一个总结，之后输出y2，所以得到的y2，不仅仅包含了输入x2，还包含了上一步的x1的记忆，也就是对x1，x2按顺序的一个总结。

下面的总体过程：

所有的w都是同一个w，经过同一个cell的时候，都会保留输入的记忆，再加上另外一个要预测的输入，所以预测包含了之前所有的记忆加上此次的输入。

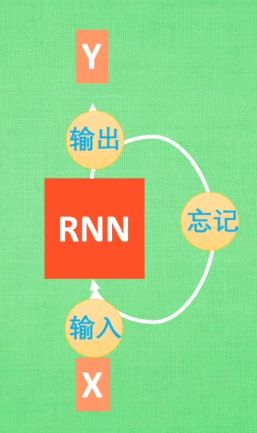
普通的RNN，如果要预测的序列是一个很长的序列，则反向传播过程中存在梯度消失和梯度爆炸现象。

为了解决上述问题，提出了 LSTM RNN

Long Short-Term Memory，长短期记忆RNN

RNN是在有序的数据上进行学习的，RNN会产生对先前发生事件的记忆，不过一般形式的RNN有些“健忘”。

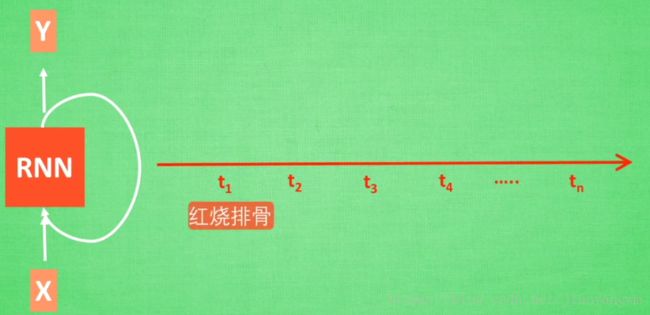
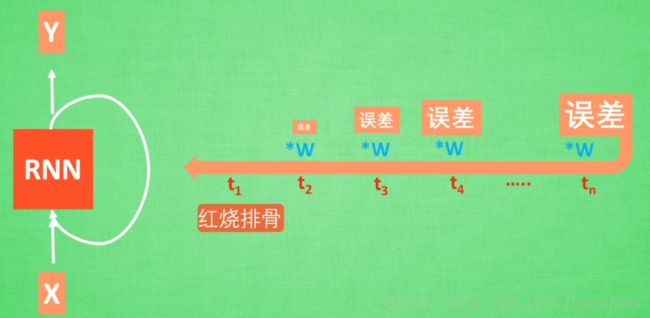
以“红烧排骨”来分析，普通RNN为什么对久远的记忆较差：

1）关键词“红烧排骨”要经过很多层训练到达输出，得到误差

2）误差反向传递时：得到的误差在每一步都会乘以系数 w w

• 如果 w<1 w < 1 ，则传递到前面的误差值就非常小，就是梯度消失
  
• 如果 w>1 w > 1 ，则传递到前面的误差值就非常大，超过了承受范围，计算梯度爆炸
  

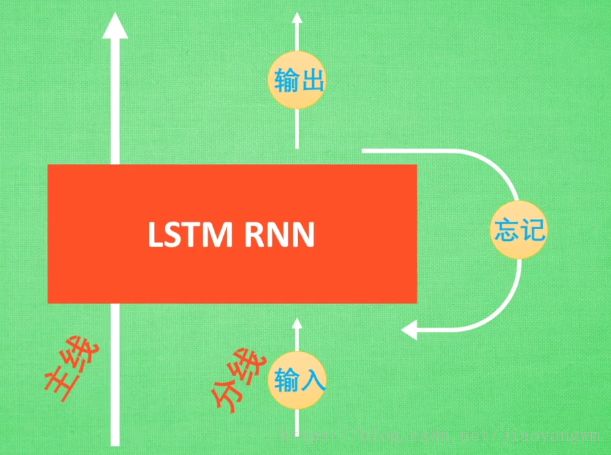
LSTM的改进：增加了三个控制器——输入控制、输出控制、忘记控制

具体介绍：

输入：考虑要不要将分线剧情加入到主线剧情，如果某些分线剧情比较重要，那么就会按重要程度，将其写入总线剧情，再进行分析。

忘记：如果分线剧情改变了我们对主线剧情的认知，那么忘记剧情就会对之前的剧情进行忘记，按比例替换为现在的新剧情。

所以主线剧情的更新就取决于输入控制和忘记控制。

输出：基于目前的主线剧情和分线剧情，判断到底要输出什么。

基于上述控制机制，LSTM就延缓了记忆衰退。

Tensorflow

以图像来说，顺序表示什么？

就是第一行的像素算起，先考虑第一行，一直到最后一行。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist=input_data.read_data_sets('MNIST_data',one_hot=True)

#hyperparameters
lr=0.1                 #learning rate
training_iters=100000    #循环次数
batch_size=128

n_inputs=28              #MNIST data input(28*28),每次输入一行，即28个像素
n_steps=28               #总共28行，即输入28次28
n_hidden_unis=128        #隐层神经元
n_classes=10             #10个类

#tf Graph input
x=tf.placeholder(tf.float32,[None,n_steps,n_inputs])
y=tf.placeholder(tf.float32,[None,n_classes])

#Define weights
#weights:input weights+output weights
#进入RNN的cell之前，要经过一层hidden layer
#cell计算完结果后再输出到output hidden layer
#下面就定义cell前后的两层hidden layer，包括weights和biases

weights={
    #(28,128)
    'in':tf.Variable(tf.random_normal([n_inputs,n_hidden_unis])),
    #(128,10)
    'out':tf.Variable(tf.random_normal([n_hidden_unis,n_classes]))
}
biases={
    #(128,)
    'in':tf.Variable(tf.constant(0.1,shape=[n_hidden_unis,])),
    #(10,)
    'out':tf.Variable(tf.constant(0.1,shape=[n_classes,]))
}

def RNN(X,weights,biases):
    #hidden layer for input to cell
    #X(128 batch,28 steps,28 inputs),要转化成(128x128,28 inputs),因为要进行矩阵乘法
    X=tf.reshape(X,[-1,n_inputs])
    # 再变换为3维矩阵,(128 batch x 28 steps,128 hidden)
    X_in=tf.matmul(X,weights['in'])+biases['in']
    # 再变换为3维矩阵,(128 batch,28 steps,128 hidden)
    X_in=tf.reshape(X_in,[-1,n_steps,n_hidden_unis])

    #cell
    #包含多少个节点，forget_bias:初始的forget定义为1，也就是不忘记，state_is_tuple：
    lstm_cell=tf.nn.rnn_cell.BasicLSTMCell(n_hidden_unis,forget_bias=1.0,state_is_tuple=True)
    #RNN每次计算一次都会保留一个state
    #LSTM会保留两个state，lstm cell is divided into two parts(c_state,m_state),
    #也就是主线的state(c_state),和分线的state(m_state)，会包含在元组（tuple）里边
    #state_is_tuple=True就是判定生成的是否为一个元组

    # 初始state,全部为0，慢慢的累加记忆
    _init_state=lstm_cell.zero_state(batch_size,dtype=tf.float32)
    #outputs是一个list，每步的运算都会保存起来，time_majortime的时间点是不是在维度为1的地方，我们的放在第二个维度，28steps
    outputs,states=tf.nn.dynamic_rnn(lstm_cell,X_in,initial_state=_init_state,time_major=False)


    #hidden layer for outputs and final results
    results=tf.matmul(states[1],weights['out'])+biases['out']
    return results


pred=RNN(x,weights,biases)
#the error between prediction and real data
#labels是神经网络目标输出 , logistics是神经网络实际输出
cost=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred,labels=y))
train_op=tf.train.AdadeltaOptimizer(lr).minimize(cost)

correct_pred=tf.equal(tf.arg_max(pred,1),tf.arg_max(y,1))
accuracy=tf.reduce_mean(tf.cast(correct_pred,tf.float32))

init=tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    step=0
    while step*batch_sizeif step%20==0:
            print(sess.run(accuracy,feed_dict={x:batch_xs,y:batch_ys}))
        step+=1

十八、自编码（Autoencoder）

神经网络的非监督学习

神经网络接收图像 → → 给图像打马赛克 → → 再还原

具体：

原有的图像被压缩，再用所储存的特征信息，经过解压获得原图。

如果神经元直接从获取的高清图像中取学习信息，会是一件很吃力的事情，所以通过特征提取，提取出能够重构出原图的主要信息，把缩减后的信息放入神经网络中进行学习，就可以更加轻松的学习。

输入：白色的X

输出：黑色的X

求取两者的误差，经过误差反向传递，逐步提升自编码准确性，中间的隐层就是能够提取出原数据最主要特征的神经元。

为什么说其是非监督学习：因为该过程只是用了X，而不用其标签，所以使非监督学习。

一般使用的时候只是用前半部分

因为前面已经学习了数据的精髓，我们只需要创建一个神经网络来学习这些精髓就好啦，可以达到和普通神经网络一样的效果，并且很高效。

编码器：前半部分

解码器：后半部分

自编码和PCA类似，可以提取出特征，可以给特征降维，自编码超越了PCA。

代码1：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist=input_data.read_data_sets('MNIST_data',one_hot=True)

#hyperparameters
lr=0.1                 #learning rate
training_iters=100000    #循环次数
batch_size=128

n_inputs=28              #MNIST data input(28*28),每次输入一行，即28个像素
n_steps=28               #总共28行，即输入28次28
n_hidden_unis=128        #隐层神经元
n_classes=10             #10个类

#tf Graph input
x=tf.placeholder(tf.float32,[None,n_steps,n_inputs])
y=tf.placeholder(tf.float32,[None,n_classes])

#Define weights
#weights:input weights+output weights
#进入RNN的cell之前，要经过一层hidden layer
#cell计算完结果后再输出到output hidden layer
#下面就定义cell前后的两层hidden layer，包括weights和biases

weights={
    #(28,128)
    'in':tf.Variable(tf.random_normal([n_inputs,n_hidden_unis])),
    #(128,10)
    'out':tf.Variable(tf.random_normal([n_hidden_unis,n_classes]))
}
biases={
    #(128,)
    'in':tf.Variable(tf.constant(0.1,shape=[n_hidden_unis,])),
    #(10,)
    'out':tf.Variable(tf.constant(0.1,shape=[n_classes,]))
}

def RNN(X,weights,biases):
    #hidden layer for input to cell
    #X(128 batch,28 steps,28 inputs),要转化成(128x128,28 inputs),因为要进行矩阵乘法
    X=tf.reshape(X,[-1,n_inputs])
    # 再变换为3维矩阵,(128 batch x 28 steps,128 hidden)
    X_in=tf.matmul(X,weights['in'])+biases['in']
    # 再变换为3维矩阵,(128 batch,28 steps,128 hidden)
    X_in=tf.reshape(X_in,[-1,n_steps,n_hidden_unis])

    #cell
    #包含多少个节点，forget_bias:初始的forget定义为1，也就是不忘记，state_is_tuple：
    lstm_cell=tf.nn.rnn_cell.BasicLSTMCell(n_hidden_unis,forget_bias=1.0,state_is_tuple=True)
    #RNN每次计算一次都会保留一个state
    #LSTM会保留两个state，lstm cell is divided into two parts(c_state,m_state),
    #也就是主线的state(c_state),和分线的state(m_state)，会包含在元组（tuple）里边
    #state_is_tuple=True就是判定生成的是否为一个元组

    # 初始state,全部为0，慢慢的累加记忆
    _init_state=lstm_cell.zero_state(batch_size,dtype=tf.float32)
    #outputs是一个list，每步的运算都会保存起来，time_majortime的时间点是不是在维度为1的地方，我们的放在第二个维度，28steps
    outputs,states=tf.nn.dynamic_rnn(lstm_cell,X_in,initial_state=_init_state,time_major=False)


    #hidden layer for outputs and final results
    results=tf.matmul(states[1],weights['out'])+biases['out']
    return results


pred=RNN(x,weights,biases)
#the error between prediction and real data
#labels是神经网络目标输出 , logistics是神经网络实际输出
cost=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred,labels=y))
train_op=tf.train.AdamOptimizer(lr).minimize(cost)

correct_pred=tf.equal(tf.arg_max(pred,1),tf.arg_max(y,1))
accuracy=tf.reduce_mean(tf.cast(correct_pred,tf.float32))

init=tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    step=0
    while step*batch_sizeif step%20==0:
            print(sess.run(accuracy,feed_dict={x:batch_xs,y:batch_ys}))
        step+=1

把梯度下降方法输入错了，cost总是很大，找了好久的问题。

结果：

Epoch: 0001 cost= 0.089918643
Epoch: 0002 cost= 0.082782879
Epoch: 0003 cost= 0.073581800
Epoch: 0004 cost= 0.069128580
Epoch: 0005 cost= 0.066503450
Epoch: 0006 cost= 0.066125013
Epoch: 0007 cost= 0.062507540
Epoch: 0008 cost= 0.059653457
Epoch: 0009 cost= 0.060695820
Epoch: 0010 cost= 0.059536964
Optimization Finished

代码2：

import tensorflow as tf
import matplotlib.pyplot as plt

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=False)

learning_rate = 0.01
training_epochs = 20
batch_size = 256
display_step = 1
n_input = 784
X = tf.placeholder("float", [None, n_input])

#压缩过程，压缩到2个元素
n_hidden_1 = 128
n_hidden_2 = 64
n_hidden_3 = 10
n_hidden_4 = 2

weights = {
    'encoder_h1': tf.Variable(tf.truncated_normal([n_input, n_hidden_1],)),
    'encoder_h2': tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2],)),
    'encoder_h3': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_3],)),
    'encoder_h4': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_4],)),
    'decoder_h1': tf.Variable(tf.truncated_normal([n_hidden_4, n_hidden_3],)),
    'decoder_h2': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_2],)),
    'decoder_h3': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_1],)),
    'decoder_h4': tf.Variable(tf.truncated_normal([n_hidden_1, n_input],)),
}
biases = {
    'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'encoder_b3': tf.Variable(tf.random_normal([n_hidden_3])),
    'encoder_b4': tf.Variable(tf.random_normal([n_hidden_4])),
    'decoder_b1': tf.Variable(tf.random_normal([n_hidden_3])),
    'decoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'decoder_b3': tf.Variable(tf.random_normal([n_hidden_1])),
    'decoder_b4': tf.Variable(tf.random_normal([n_input])),
}
def encoder(x):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h1']),
                                   biases['encoder_b1']))
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h2']),
                                   biases['encoder_b2']))
    layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['encoder_h3']),
                                   biases['encoder_b3']))
    # 为了便于编码层的输出，编码层随后一层不使用激活函数，输出的范围是无穷大
    layer_4 = tf.add(tf.matmul(layer_3, weights['encoder_h4']),
                                    biases['encoder_b4'])
    return layer_4

def decoder(x):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h1']),
                                   biases['decoder_b1']))
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']),
                                   biases['decoder_b2']))
    layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['decoder_h3']),
                                biases['decoder_b3']))
    layer_4 = tf.nn.sigmoid(tf.add(tf.matmul(layer_3, weights['decoder_h4']),
                                biases['decoder_b4']))
    return layer_4

encoder_op = encoder(X)
decoder_op = decoder(encoder_op)

y_pred = decoder_op
y_true = X

cost = tf.reduce_mean(tf.pow(y_true - y_pred, 2))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)

init=tf.global_variables_initializer()

with tf.Session() as sess:

    sess.run(init)
    total_batch = int(mnist.train.num_examples/batch_size)
    for epoch in range(training_epochs):
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)  # max(x) = 1, min(x) = 0
            _, c = sess.run([optimizer, cost], feed_dict={X: batch_xs})
        if epoch % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(c))
    print("Optimization Finished!")

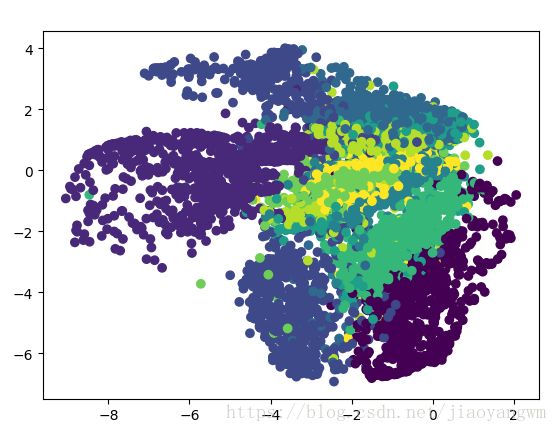
    #显示解压前的结果
    encoder_result = sess.run(encoder_op, feed_dict={X: mnist.test.images})
    plt.scatter(encoder_result[:, 0], encoder_result[:, 1], c=mnist.test.labels)
    # plt.colorbar()
    plt.show()

结果：

十九、tf.name_scope / tf.variable_scope

一、tf.name_scope

from __future__ import print_function
#__future__模块，把下一个新版本的特性导入到当前版本，于是我们就可以在当前版本中测试一些新版本的特性
import tensorflow as tf
tf.set_random_seed(1)


with tf.name_scope("a_name_scope"):       #name_scope的名字为"a_name_scope"
    initializer=tf.constant_initializer(value=1)
    #两种创建variable的途径
    # tf.get_variable要定义一个initializer
    # name_scope 对tf.get_variable无效
    var1=tf.get_variable(name='var1',shape=[1],dtype=tf.float32,initializer=initializer)

    var2=tf.Variable(name='var2', initial_value=[2], dtype=tf.float32)
    var21 = tf.Variable(name='var2', initial_value=[2.1], dtype=tf.float32)
    var22 = tf.Variable(name='var2', initial_value=[2.2], dtype=tf.float32)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    #分别打印varibale的名字和值
    print(var1.name)
    print(sess.run(var1))
    print(var2.name)
    print(sess.run(var2))
    print(var21.name)
    print(sess.run(var21))
    print(var22.name)
    print(sess.run(var22))

结果：

var1:0
[ 1.]
a_name_scope/var2:0
[ 2.]
a_name_scope/var2_1:0
[ 2.0999999]
a_name_scope/var2_2:0
[ 2.20000005]

二、tf.variable_scope

from __future__ import print_function
#__future__模块，把下一个新版本的特性导入到当前版本，于是我们就可以在当前版本中测试一些新版本的特性
import tensorflow as tf
tf.set_random_seed(1)

with tf.variable_scope("a_variable_scope") as scope:
    initializer=tf.constant_initializer(value=3)
    var3=tf.get_variable(name="var3",shape=[1],dtype=tf.float32,initializer=initializer)
    var4=tf.Variable(name='var4',initial_value=[4],dtype=tf.float32)
    #可以重复调用之前创造的变量，但是tf.Variable是不可行的，只能重新创建一个
    #a_variable_scope/var4:0
    # [ 4.]
    # a_variable_scope/var4_1:0
    # [ 4.]
    #var4_reuse=tf.Variable(name='var4',initial_value=[4],dtype=tf.float32)

    #使用tf.get_variable重复调用var3,要先强调后面的要重复利用
    #scope.reuse_variables()会先再前面搜索是否已经存在，重复利用得到的两个变量是同一个变量
    scope.reuse_variables()
    var3_reuse=tf.get_variable(name='var3')

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    #分别打印varibale的名字和值
    print(var3.name)
    print(sess.run(var3))
    print(var4.name)
    print(sess.run(var4))
    print(var3_reuse.name)
    print(sess.run(var3_reuse))

结果：

a_variable_scope/var3:0
[ 3.]
a_variable_scope/var4:0
[ 4.]
a_variable_scope/var3:0
[ 3.]

为什么要用tf.variable_scope来定义重复利用？

——RNN会经常用到。

二十、批标准化——Batch Normalization

将分散的数据进行规范化，利于机器学习的学习。

数据分布会对神经网络的学习产生影响，

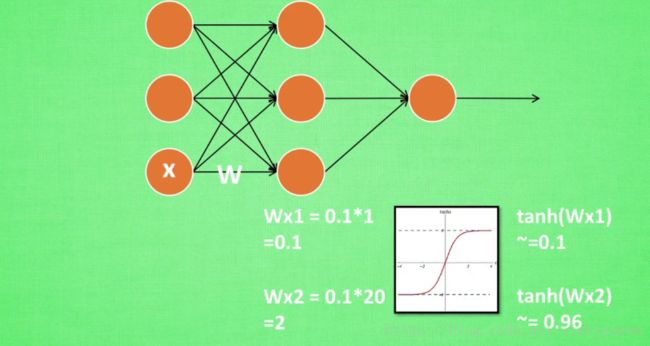
1）输入X1=1，权值为W=0.1，第二层接收到的就是 Wx1=0.1∗1=0.1 W x 1 = 0.1 ∗ 1 = 0.1

2）输入X2=20，权值为W=0.1，第二层接收到的就是 Wx1=0.1∗20=2 W x 1 = 0.1 ∗ 20 = 2

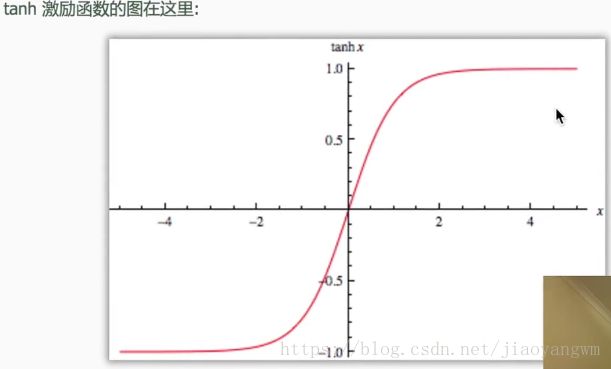
3）添加激活函数：tanh， tanh(x1)=0.1 t a n h ( x 1 ) = 0.1 ， tanh(x2)=0.96 t a n h ( x 2 ) = 0.96 ，x2已经接近饱和了，无论之后x怎么扩大，tanh函数的输出值都不会变化很大，也就是神经网络在初始阶段已经不对那些过大的x敏感了，所以要做预处理，使得输入的范围规范化，集中在激励函数的敏感部分。

但是这种情况不仅仅发生在输入层，同样发生在隐藏层，那么可以对隐藏层的输入进行标准化吗？

答案是肯定的，这也叫做batch normalization

将数据Data进行分批，分批进行随机梯度下降，并且在每批数据进行前向传递的时候，对每一层都进行Normaliation。

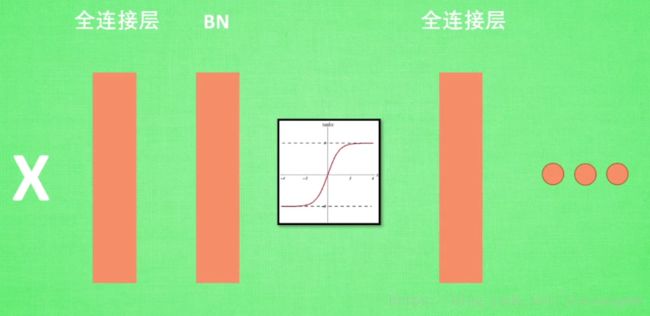
x经过神经网络的前向传播过程：

x->全连接层->激活函数->全连接层

添加Batch Normalization：

x->全连接层->Batch Normalization->激活函数->全连接层

输入激励函数的值对计算结果很重要，所以要将数据规范化到激活函数的敏感区域，才能更有效的向前传递。

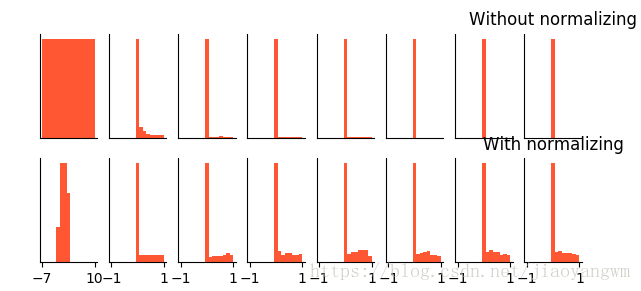
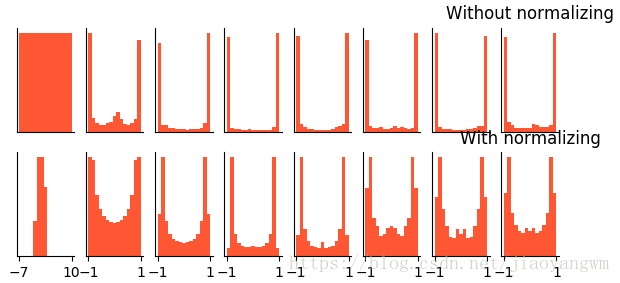
下图展示了未进行BN 和进行BN后的数据的分布：

激活后的分布如下：

未进行BN的数据激活之后大多分布在饱和阶段，也就是-1和1的居多，BN之后的数据进行激活的结果基本均匀分布，对神经网络的学习更加有价值。

Batch Normalization：包含正向和反向两个过程

反向操作：将BN后的数据进行扩展和平移，就是为了让神经网络自己学习去学习使用和修改扩展参数 γ γ ，和平移参数 β β ，让神经网络自己学习BN到底有没有作用，如果没有作用的话，就用上述两个参数进行抵消BN的一些操作。

神经网络训练到最后，数据的分布图

有BN标准化：让每一层的值在有效的范围内传递下去，

无BN标准化：缺失了对数据的敏感性，不能有效的传递每一层的信息

详细解释：

上面一行是未进行BN的过程：

下面一行是对每一层都进行BN的过程：

Tensorflow

"""
Build two networks.
1. Without batch normalization
2. With batch normalization

Run tests on these two networks.
"""

# 23 Batch Normalization

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt


ACTIVATION = tf.nn.tanh
N_LAYERS = 7
N_HIDDEN_UNITS = 30


def fix_seed(seed=1):
    # reproducible
    np.random.seed(seed)
    tf.set_random_seed(seed)


def plot_his(inputs, inputs_norm):
    # plot histogram for the inputs of every layer
    for j, all_inputs in enumerate([inputs, inputs_norm]):
        for i, input in enumerate(all_inputs):
            plt.subplot(2, len(all_inputs), j*len(all_inputs)+(i+1))
            plt.cla()
            if i == 0:
                the_range = (-7, 10)
            else:
                the_range = (-1, 1)
            plt.hist(input.ravel(), bins=15, range=the_range, color='#FF5733')
            plt.yticks(())
            if j == 1:
                plt.xticks(the_range)
            else:
                plt.xticks(())
            ax = plt.gca()
            ax.spines['right'].set_color('none')
            ax.spines['top'].set_color('none')
        plt.title("%s normalizing" % ("Without" if j == 0 else "With"))
    plt.draw()
    plt.pause(0.01)


def built_net(xs, ys, norm):
    def add_layer(inputs, in_size, out_size, activation_function=None, norm=False):
        # weights and biases (bad initialization for this case)
        Weights = tf.Variable(tf.random_normal([in_size, out_size], mean=0., stddev=1.))
        biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)

        # fully connected product
        Wx_plus_b = tf.matmul(inputs, Weights) + biases

        # normalize fully connected product
        if norm:
            # Batch Normalize
            # 首先得到整批数据的均值和方差，在batch的维度上
            #注意！如果是test，要固定fc_mean, fc_var两个参数，不使用tf.nn.moments
            #因为测试的时候不是在一个batch中测试的，不用求它的方差均值了
            fc_mean, fc_var = tf.nn.moments(
                Wx_plus_b,
                axes=[0],   # the dimension you wanna normalize, here [0] for batch
                            # for image, you wanna do [0, 1, 2] for [batch, height, width] but not channel
            )
            scale = tf.Variable(tf.ones([out_size]))
            shift = tf.Variable(tf.zeros([out_size]))
            epsilon = 0.001

            # apply moving average for mean and var when train on batch
            ema = tf.train.ExponentialMovingAverage(decay=0.5)
            def mean_var_with_update():
                ema_apply_op = ema.apply([fc_mean, fc_var])
                with tf.control_dependencies([ema_apply_op]):
                    return tf.identity(fc_mean), tf.identity(fc_var)
            mean, var = mean_var_with_update()

            Wx_plus_b = tf.nn.batch_normalization(Wx_plus_b, mean, var, shift, scale, epsilon)
            # similar with this two steps:
            # Wx_plus_b = (Wx_plus_b - fc_mean) / tf.sqrt(fc_var + 0.001)
            # Wx_plus_b = Wx_plus_b * scale + shift

        # activation
        if activation_function is None:
            outputs = Wx_plus_b
        else:
            outputs = activation_function(Wx_plus_b)

        return outputs

    fix_seed(1)
    #对输入层做normalization
    if norm:
        # BN for the first input
        fc_mean, fc_var = tf.nn.moments(
            xs,
            axes=[0],
        )
        scale = tf.Variable(tf.ones([1]))
        shift = tf.Variable(tf.zeros([1]))
        epsilon = 0.001
        # apply moving average for mean and var when train on batch
        ema = tf.train.ExponentialMovingAverage(decay=0.5)
        def mean_var_with_update():
            ema_apply_op = ema.apply([fc_mean, fc_var])
            with tf.control_dependencies([ema_apply_op]):
                return tf.identity(fc_mean), tf.identity(fc_var)
        mean, var = mean_var_with_update()
        xs = tf.nn.batch_normalization(xs, mean, var, shift, scale, epsilon)

    # record inputs for every layer
    layers_inputs = [xs]

    # build hidden layers
    for l_n in range(N_LAYERS):
        layer_input = layers_inputs[l_n]
        in_size = layers_inputs[l_n].get_shape()[1].value

        output = add_layer(
            layer_input,    # input
            in_size,        # input size
            N_HIDDEN_UNITS, # output size
            ACTIVATION,     # activation function
            norm,           # normalize before activation
        )
        layers_inputs.append(output)    # add output for next run

    # build output layer
    prediction = add_layer(layers_inputs[-1], 30, 1, activation_function=None)

    cost = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))
    train_op = tf.train.GradientDescentOptimizer(0.001).minimize(cost)
    return [train_op, cost, layers_inputs]

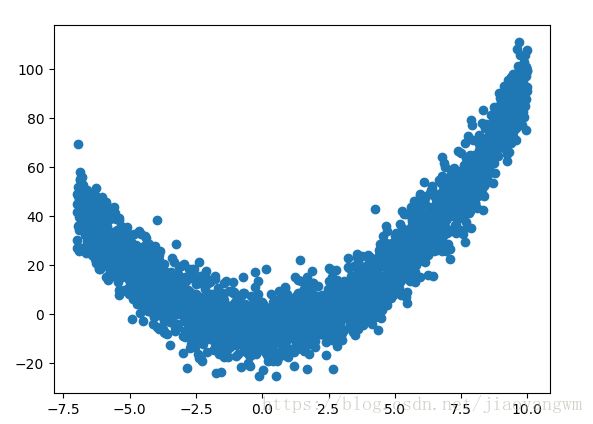
# make up data
fix_seed(1)
x_data = np.linspace(-7, 10, 2500)[:, np.newaxis]
np.random.shuffle(x_data)
noise = np.random.normal(0, 8, x_data.shape)
y_data = np.square(x_data) - 5 + noise

# plot input data
plt.scatter(x_data, y_data)
plt.show()

xs = tf.placeholder(tf.float32, [None, 1])  # [num_samples, num_features]
ys = tf.placeholder(tf.float32, [None, 1])

train_op, cost, layers_inputs = built_net(xs, ys, norm=False)   # without BN
train_op_norm, cost_norm, layers_inputs_norm = built_net(xs, ys, norm=True) # with BN

sess = tf.Session()
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
    init = tf.initialize_all_variables()
else:
    init = tf.global_variables_initializer()
sess.run(init)

# record cost
cost_his = []
cost_his_norm = []
record_step = 5

plt.ion()
plt.figure(figsize=(7, 3))
for i in range(250):
    if i % 50 == 0:
        # plot histogram
        all_inputs, all_inputs_norm = sess.run([layers_inputs, layers_inputs_norm], feed_dict={xs: x_data, ys: y_data})
        plot_his(all_inputs, all_inputs_norm)

    # train on batch
    sess.run([train_op, train_op_norm], feed_dict={xs: x_data[i*10:i*10+10], ys: y_data[i*10:i*10+10]})

    if i % record_step == 0:
        # record cost
        cost_his.append(sess.run(cost, feed_dict={xs: x_data, ys: y_data}))
        cost_his_norm.append(sess.run(cost_norm, feed_dict={xs: x_data, ys: y_data}))

plt.ioff()
plt.figure()
plt.plot(np.arange(len(cost_his))*record_step, np.array(cost_his), label='no BN')     # no norm
plt.plot(np.arange(len(cost_his))*record_step, np.array(cost_his_norm), label='BN')   # norm
plt.legend()
plt.show()

每50步变化一次的分布情况，

没有BN的情况：第一层还有分布，后面的基本都变为0。
输入（-7，10）

有BN的情况：基本上都可以很好的分布在大于0的区间。
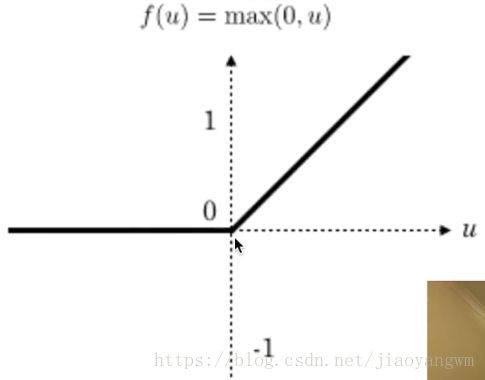
使用的relu的激活函数：

误差曲线：

no BN的误差曲线都没有，训练到最后，所有的神经元都不起作用了，说明用relu函数后，都不起作用了。

tanh

数据分布：

没有BN：输入值基本趋于饱和

有BN：大部分值都在没有饱和的区间，也就是激活的状态

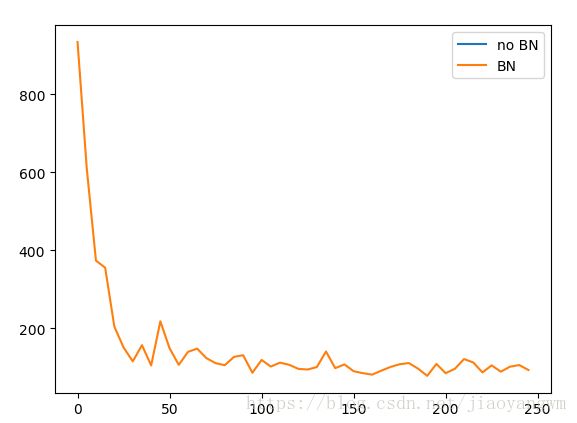
误差曲线：

no BN：有误差曲线了

BN：误差会一直减小，训练效果更好

二十一、可视化梯度

import tensorflow as tf
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

LR=0.1
#模型有两个参数
REAL_PARAMS=[1.2,2.5]  #生成模型的真实参数
INIT_PARAMS=[[5,4],    #初始化的数据
             [5,1],
             [2,4.5]][2]

x=np.linspace(-1,1,200,dtype=np.float32)

# test 1
y_fun=lambda a,b:a*x+b      #生成真实数据
tf_y_fun=lambda a,b:a*x+b   #用tensorflow来拟合a和b这两个参数

noise=np.random.rand(200)/10
y=y_fun(*REAL_PARAMS)+noise  #参数使用REAL_PARAMS
# plt.scatter(x,y)
# plt.show()

a,b=[tf.Variable(initial_value=p,dtype=tf.float32) for p in INIT_PARAMS]
pred=tf_y_fun(a,b)
mse=tf.reduce_mean(tf.square(y-pred))
train_op=tf.train.GradientDescentOptimizer(LR).minimize(mse)

a_list,b_list,cost_list=[],[],[]
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for t in range(400):
        a_,b_,mes_=sess.run([a,b,mse])
        #record parameters
        a_list.append(a_)
        b_list.append(b_)
        cost_list.append(mes_)
        #training
        result,_=sess.run([pred,train_op])

# visualization codes:
print('a=', a_, 'b=', b_)
plt.figure(1)
plt.scatter(x, y, c='b')    # plot data
plt.plot(x, result, 'r-', lw=2)   # plot line fitting
# 3D cost figure
fig = plt.figure(2); ax = Axes3D(fig)
a3D, b3D = np.meshgrid(np.linspace(-2, 7, 30), np.linspace(-2, 7, 30))  # parameter space
cost3D = np.array([np.mean(np.square(y_fun(a_, b_) - y)) for a_, b_ in zip(a3D.flatten(), b3D.flatten())]).reshape(a3D.shape)
ax.plot_surface(a3D, b3D, cost3D, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'), alpha=0.5)
ax.scatter(a_list[0], b_list[0], zs=cost_list[0], s=300, c='r')  # initial parameter place
ax.set_xlabel('a'); ax.set_ylabel('b')
ax.plot(a_list, b_list, zs=cost_list, zdir='z', c='r', lw=3)    # plot 3D gradient descent
plt.show()

结果：

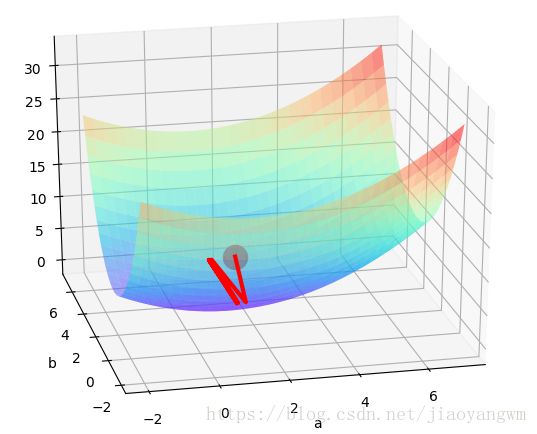
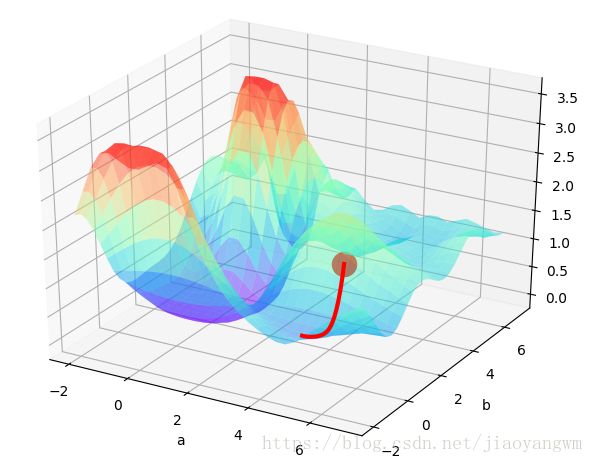
a= 1.19776 b= 2.54675

从初始点向误差小的方向下降

跨步太大，路径波动太大，出现震荡。

并且没有办法很好的拟合到原始数据

如何使用Tensorflow进行调参：

局部最优：和初始值关系较大，会滑到局部最小值

初始点1：

LR=0.1
#模型有两个参数
REAL_PARAMS=[1.2,2.5]  #生成模型的真实参数
INIT_PARAMS=[[5,4],    #初始化的数据
             [5,1],
             [2,4.5]][2]

初始点2：改变初始值

#模型有两个参数
REAL_PARAMS=[1.2,2.5]  #生成模型的真实参数
INIT_PARAMS=[[5,4],    #初始化的数据
             [5,1],
             [2,4.5]][1]

二十二：迁移学习——Transfer learning

站在巨人的肩膀上，借鉴已有的模型。

不再训练前面的参数，也就是固定住模型的理解能力，将输出层替换为需要的功能。

节约计算资源

Tensorflow实现：

利用16层的VGGNet，拆掉其分类的部分，补上用回归的。

区分猫和老虎。

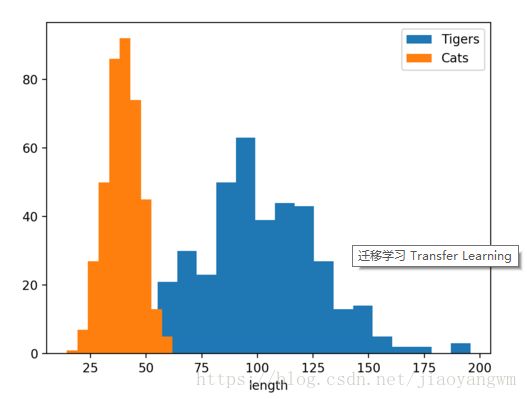
原本为分类，现在做成回归，就是做些假的数据，包括猫和老虎自身的长度，

我们就来迁移一个图片分类的 CNN (VGG). 这个 VGG 在1000个类别中训练过. 我们提取这个 VGG 前面的 Conv layers, 重新组建后面的 fully connected layers, 让它做一个和分类完全不相干的事. 我们在网上下载那1000个分类数据中的猫和老虎的图片, 然后伪造一些猫和老虎长度的数据. 最后做到让迁移后的网络分辨出猫和老虎的长度 (regressor).

因为现在我们不是预测分类结果了, 所以我伪造了一些体长的数据. 老虎通常要比猫长, 所以它们的 distribution 就差不多是下面这种结构(单位cm).

数据下载：

VGG16.npy

迁移学习改动的地方：

为了做迁移学习, 对他的 tensorflow VGG16 代码进行了改写. 保留了所有 Conv 和 pooling 层, 将后面的所有 fc 层拆了, 改成可以被 train 的两层, 输出一个数字, 这个数字代表了这只猫或老虎的长度.

"""
This is a simple example of transfer learning using VGG.
Fine tune a CNN from a classifier to regressor.
Generate some fake data for describing cat and tiger length.
Fake length setting:
Cat - Normal distribution (40, 8)
Tiger - Normal distribution (100, 30)
The VGG model and parameters are adopted from:
https://github.com/machrisaa/tensorflow-vgg
Learn more, visit my tutorial site: [莫烦Python](https://morvanzhou.github.io)
"""

from urllib.request import urlretrieve
import os
import numpy as np
import tensorflow as tf
import skimage.io
import skimage.transform
import matplotlib.pyplot as plt


def download():     # download tiger and kittycat image
    categories = ['tiger', 'kittycat']
    for category in categories:
        os.makedirs('transfer_learning/data/%s' % category, exist_ok=True)
        with open('transfer_learning/model/imagenet_%s.txt' % category, 'r') as file:
            urls = file.readlines()
            n_urls = len(urls)
            for i, url in enumerate(urls):
                try:
                    urlretrieve(url.strip(), 'transfer_learning/data/%s/%s' % (category, url.strip().split('/')[-1]))
                    print('%s %i/%i' % (category, i, n_urls))
                except:
                    print('%s %i/%i' % (category, i, n_urls), 'no image')


def load_img(path):
    img = skimage.io.imread(path)
    img = img / 255.0
    # print "Original Image Shape: ", img.shape
    # we crop image from center
    short_edge = min(img.shape[:2])
    yy = int((img.shape[0] - short_edge) / 2)
    xx = int((img.shape[1] - short_edge) / 2)
    crop_img = img[yy: yy + short_edge, xx: xx + short_edge]
    # resize to 224, 224
    resized_img = skimage.transform.resize(crop_img, (224, 224))[None, :, :, :]   # shape [1, 224, 224, 3]
    return resized_img


def load_data():
    imgs = {'tiger': [], 'kittycat': []}
    for k in imgs.keys():
        dir = 'transfer_learning/data/' + k
        for file in os.listdir(dir):
            if not file.lower().endswith('.jpg'):
                continue
            try:
                resized_img = load_img(os.path.join(dir, file))
            except OSError:
                continue
            imgs[k].append(resized_img)    # [1, height, width, depth] * n
            if len(imgs[k]) == 400:        # only use 400 imgs to reduce my memory load
                break
    # fake length data for tiger and cat
    tigers_y = np.maximum(20, np.random.randn(len(imgs['tiger']), 1) * 30 + 100)
    cat_y = np.maximum(10, np.random.randn(len(imgs['kittycat']), 1) * 8 + 40)
    return imgs['tiger'], imgs['kittycat'], tigers_y, cat_y


class Vgg16:
    vgg_mean = [103.939, 116.779, 123.68]

    def __init__(self, vgg16_npy_path=None, restore_from=None):
        # pre-trained parameters
        try:
            self.data_dict = np.load(vgg16_npy_path, encoding='latin1').item()
        except FileNotFoundError:
            print('Please download VGG16 parameters at here https://mega.nz/#!YU1FWJrA!O1ywiCS2IiOlUCtCpI6HTJOMrneN-Qdv3ywQP5poecM')

        self.tfx = tf.placeholder(tf.float32, [None, 224, 224, 3])
        self.tfy = tf.placeholder(tf.float32, [None, 1])

        # Convert RGB to BGR
        red, green, blue = tf.split(axis=3, num_or_size_splits=3, value=self.tfx * 255.0)
        bgr = tf.concat(axis=3, values=[
            blue - self.vgg_mean[0],
            green - self.vgg_mean[1],
            red - self.vgg_mean[2],
        ])

        # pre-trained VGG layers are fixed in fine-tune
        conv1_1 = self.conv_layer(bgr, "conv1_1")
        conv1_2 = self.conv_layer(conv1_1, "conv1_2")
        pool1 = self.max_pool(conv1_2, 'pool1')

        conv2_1 = self.conv_layer(pool1, "conv2_1")
        conv2_2 = self.conv_layer(conv2_1, "conv2_2")
        pool2 = self.max_pool(conv2_2, 'pool2')

        conv3_1 = self.conv_layer(pool2, "conv3_1")
        conv3_2 = self.conv_layer(conv3_1, "conv3_2")
        conv3_3 = self.conv_layer(conv3_2, "conv3_3")
        pool3 = self.max_pool(conv3_3, 'pool3')

        conv4_1 = self.conv_layer(pool3, "conv4_1")
        conv4_2 = self.conv_layer(conv4_1, "conv4_2")
        conv4_3 = self.conv_layer(conv4_2, "conv4_3")
        pool4 = self.max_pool(conv4_3, 'pool4')

        conv5_1 = self.conv_layer(pool4, "conv5_1")
        conv5_2 = self.conv_layer(conv5_1, "conv5_2")
        conv5_3 = self.conv_layer(conv5_2, "conv5_3")
        pool5 = self.max_pool(conv5_3, 'pool5')

        # detach original VGG fc layers and
        # reconstruct your own fc layers serve for your own purpose
        self.flatten = tf.reshape(pool5, [-1, 7*7*512])
        self.fc6 = tf.layers.dense(self.flatten, 256, tf.nn.relu, name='fc6')
        self.out = tf.layers.dense(self.fc6, 1, name='out')

        self.sess = tf.Session()
        if restore_from:
            saver = tf.train.Saver()
            saver.restore(self.sess, restore_from)
        else:   # training graph
            self.loss = tf.losses.mean_squared_error(labels=self.tfy, predictions=self.out)
            self.train_op = tf.train.RMSPropOptimizer(0.001).minimize(self.loss)
            self.sess.run(tf.global_variables_initializer())

    def max_pool(self, bottom, name):
        return tf.nn.max_pool(bottom, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME', name=name)

    def conv_layer(self, bottom, name):
        with tf.variable_scope(name):   # CNN's filter is constant, NOT Variable that can be trained
            conv = tf.nn.conv2d(bottom, self.data_dict[name][0], [1, 1, 1, 1], padding='SAME')
            lout = tf.nn.relu(tf.nn.bias_add(conv, self.data_dict[name][1]))
            return lout

    def train(self, x, y):
        loss, _ = self.sess.run([self.loss, self.train_op], {self.tfx: x, self.tfy: y})
        return loss

    def predict(self, paths):
        fig, axs = plt.subplots(1, 2)
        for i, path in enumerate(paths):
            x = load_img(path)
            length = self.sess.run(self.out, {self.tfx: x})
            axs[i].imshow(x[0])
            axs[i].set_title('Len: %.1f cm' % length)
            axs[i].set_xticks(()); axs[i].set_yticks(())
        plt.show()

    def save(self, path='ransfer_learning/model/transfer_learn'):
        saver = tf.train.Saver()
        saver.save(self.sess, path, write_meta_graph=False)


def train():
    tigers_x, cats_x, tigers_y, cats_y = load_data()

    # plot fake length distribution
    plt.hist(tigers_y, bins=20, label='Tigers')
    plt.hist(cats_y, bins=10, label='Cats')
    plt.legend()
    plt.xlabel('length')
    plt.show()

    xs = np.concatenate(tigers_x + cats_x, axis=0)
    ys = np.concatenate((tigers_y, cats_y), axis=0)

    vgg = Vgg16(vgg16_npy_path='transfer_learning/vgg16.npy')
    print('Net built')
    for i in range(100):
        b_idx = np.random.randint(0, len(xs), 6)
        train_loss = vgg.train(xs[b_idx], ys[b_idx])
        print(i, 'train loss: ', train_loss)

    vgg.save('transfer_learning/model/transfer_learn')      # save learned fc layers


def eval():
    vgg = Vgg16(vgg16_npy_path='transfer_learning/vgg16.npy',
                restore_from='transfer_learning/model/transfer_learn')
    vgg.predict(
        ['transfer_learning/data/kittycat/000129037.jpg', 'transfer_learning/data/tiger/391412.jpg'])


if __name__ == '__main__':
    download()
    train()
    eval()