基于tensorflow的RNN自然语言建模
关于循环神经网络的介绍可以参考:
https://blog.csdn.net/lilong117194/article/details/82958326
这里强烈建议先搞明白上述参考链接中的一些基本概念和例子,再读下面的代码。
PTB 数据集下载:http://www.fit.vutbr.cz/~imikolov/rnnlm/simple-examples.tgz
1. 自然语言建模
简单的说,自然语言建模的目的就是为了计算一个句子出现的概率。在这里把句子看做是单词的序列,于是自然语言模型需要计算的就是 p ( w 1 , w 2 , . . w n ) p(w_1,w_2,..w_n) p(w1,w2,..wn)。然后利用语言模型,可以确定哪个单词序列出现的可能性更大,或者给定若干个单词,可以预测下一个最可能出现的词语。
举个音字转换的例子:假设输入的拼音字符串为“xianzaiquna”,它的输出可以是“西安在去哪”,同样也可以是“现在去哪”。根据语言常识可以知道,应该转换为后者的概率更大,而这时的语言模型就可以得到后者的概率大于前者,这就是语言模型的作用。
那么如何计算一个句子的概率呢?首先一个句子可以被看做单词组成的序列:
s = ( w 1 , w 2 , w 3 . . . w m ) s = (w_1,w_2,w_3 ... w_m) s=(w1,w2,w3...wm)
其中 m 是下标,表示句子的长度。那么,它的概率可以表示成:
p ( s ) = p ( w 1 , w 2 , w 3 . . . w m ) = p ( w 1 ) p ( w 2 ∣ w 1 ) p ( w 3 ∣ w 1 , w 2 ) . . . p ( w m ∣ w 1 , w 2 , . . . , w m − 1 ) p(s) = p(w_1,w_2,w_3 ... w_m) = p(w_1)p(w_2|w_1)p(w_3|w_1,w_2) ... p(w_m|w_1,w_2, ... ,w_{m-1}) p(s)=p(w1,w2,w3...wm)=p(w1)p(w2∣w1)p(w3∣w1,w2)...p(wm∣w1,w2,...,wm−1)
要计算句子出现的概率,就得知道上面公式中等式右边每一项的取值。但是任何一门语言的词汇量都是极大的,这样我们无法根据这个公式计算概率,因为计算复杂度无可估量。于是我们采用估算的方法,常用的是:n-gram方法、决策树、最大熵模型、条件随机场、神经网络语言模型。这里只介绍 n-gram 模型和循环神经网络的方法。
1.1 n-gram 模型的及其评价标准
n-gram 模型基于一个重要的有限历史假设:当前单词出现的概率仅仅取决于它的前 n-1 个单词,即 p ( w m ∣ w 1 , w 2 , . . . , w m − 1 ) ≈ p ( w i ∣ w i − n + 1 , . . . , w i − 1 ) p(w_m|w_1,w_2, ... ,w_{m-1})\approx p(w_i|w_{i-n+1}, ... ,w_{i-1}) p(wm∣w1,w2,...,wm−1)≈p(wi∣wi−n+1,...,wi−1)因此上面的P(S)可以近似为 p ( S ) = p ( w 1 , w 2 , w 3 . . . w m ) = ∏ i m p ( w i ∣ w i − n + 1 , . . . , w i − 1 ) p(S) = p(w_1,w_2,w_3 ... w_m) =\prod _i ^m p(w_i|w_{i-n+1}, ... ,w_{i-1}) p(S)=p(w1,w2,w3...wm)=∏imp(wi∣wi−n+1,...,wi−1),而这里通常 n 指的是当前单词依赖它前面的单词个数。通常可以取 1,2,3 对应的模型分别称为 unigram,bigram和 trigram 模型。所以n—gram模型需要估计的参数为条件概率: p ( w i ∣ w i − n + 1 , . . . , w i − 1 ) p(w_i|w_{i-n+1}, ... ,w_{i-1}) p(wi∣wi−n+1,...,wi−1),所以有:
- 在1-gram模型下:
P ( w 1 , w 2 , w 3 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 w 2 ) P ( w 4 ∣ w 1 w 2 w 3 ) … P ( w n ∣ w 1 w 2 … w n − 1 ) ≈ P ( w 1 ) P ( w 2 ) P ( w 3 ) P ( w 4 ) … P ( w n ) P(w_1, w_2, w_3, … , w_n)=P(w_1)P(w_2|w_1)P(w_3|w_1w_2)P(w_4|w_1w_2w_3)…P(w_n|w_1w_2…w_{n-1})≈P(w_1)P(w_2)P(w_3)P(w_4)…P(w_n) P(w1,w2,w3,…,wn)=P(w1)P(w2∣w1)P(w3∣w1w2)P(w4∣w1w2w3)…P(wn∣w1w2…wn−1)≈P(w1)P(w2)P(w3)P(w4)…P(wn) - 在2-gram模型下:
P ( w 1 , w 2 , w 3 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 w 2 ) P ( w 4 ∣ w 1 w 2 w 3 ) … P ( w n ∣ w 1 w 2 … w n − 1 ) ≈ P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 2 ) P ( w 4 ∣ w 3 ) … P ( w n ∣ w n − 1 ) P(w_1, w_2, w_3, … , w_n)=P(w_1)P(w_2|w_1)P(w_3|w_1w_2)P(w_4|w_1w_2w_3)…P(w_n|w_1w_2…w_{n-1})≈P(w_1)P(w_2|w_1)P(w_3|w_2)P(w_4|w_3)…P(w_n|w_{n-1}) P(w1,w2,w3,…,wn)=P(w1)P(w2∣w1)P(w3∣w1w2)P(w4∣w1w2w3)…P(wn∣w1w2…wn−1)≈P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3)…P(wn∣wn−1) - 在3-gram模型下:
P ( w 1 , w 2 , w 3 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 w 2 ) P ( w 4 ∣ w 1 w 2 w 3 ) … P ( w n ∣ w 1 w 2 … w n − 1 ) ≈ P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 w 2 ) P ( w 4 ∣ w 2 w 3 ) … P ( w n ∣ w n − 2 w n − 1 ) P(w_1, w_2, w_3, … , w_n)=P(w_1)P(w_2|w_1)P(w_3|w_1w_2)P(w_4|w_1w_2w_3)…P(w_n|w_1w_2…w_{n-1}) ≈P(w_1)P(w_2|w_1)P(w_3|w_1w_2)P(w_4|w_2w_3)…P(w_n|w_{n-2}w_{n-1}) P(w1,w2,w3,…,wn)=P(w1)P(w2∣w1)P(w3∣w1w2)P(w4∣w1w2w3)…P(wn∣w1w2…wn−1)≈P(w1)P(w2∣w1)P(w3∣w1w2)P(w4∣w2w3)…P(wn∣wn−2wn−1) - 在4-gram模型下:
P ( w 1 , w 2 , w 3 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 w 2 ) P ( w 4 ∣ w 1 w 2 w 3 ) … P ( w n ∣ w 1 w 2 … w n − 1 ) ≈ P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 w 2 ) P ( w 4 ∣ w 1 w 2 w 3 ) … P ( w n ∣ w n − 3 w n − 2 w n − 1 ) P(w_1, w_2, w_3, … , w_n)=P(w_1)P(w_2|w_1)P(w_3|w_1w_2)P(w_4|w_1w_2w_3)…P(w_n|w_1w_2…w_{n-1})≈P(w_1)P(w_2|w_1)P(w_3|w_1w_2)P(w_4|w_1w_2w_3)…P(w_n|w_{n-3}w_{n-2}w_{n-1}) P(w1,w2,w3,…,wn)=P(w1)P(w2∣w1)P(w3∣w1w2)P(w4∣w1w2w3)…P(wn∣w1w2…wn−1)≈P(w1)P(w2∣w1)P(w3∣w1w2)P(w4∣w1w2w3)…P(wn∣wn−3wn−2wn−1)
假设某种语言的单词表大小为 k,那么我们可以计算出 n-gram 模型需要估计的不同参数数量为k的n次方(庆幸不是k的k次方)。高于四元的用的很少,因为训练它需要更庞大的语料,而且数据稀疏严重,时间复杂度高,精确度却提高的不多。而n-gram模型的参数估计一般采用最大似然估计(maximun likelihood estimation,MLE)的计算方法:
p ( w i ∣ w i − n + 1 , . . . , w i − 1 ) = C ( w i , w i − n + 1 , . . . , w i − 1 ) C ( w i − n + 1 , . . . , w i − 1 ) p(w_i|w_{i-n+1}, ... ,w_{i-1})=\frac{C(w_i,w_{i-n+1}, ... ,w_{i-1})}{C(w_{i-n+1}, ... ,w_{i-1})} p(wi∣wi−n+1,...,wi−1)=C(wi−n+1,...,wi−1)C(wi,wi−n+1,...,wi−1)
其中 C ( X ) C(X) C(X)表示单词序列X在训练语料中出现的次数。也就是说,训练语料越大,参数估计的结果越可靠。但是还有一个问题存在,那就是即使训练的语料再大,也会有在训练中没有出现过的n-gram 序列出现,这就会导致很多参数为0,为了避免乘以0而导致整个概率为0,使用最大似然估计方法时都需要加入平滑避免参数取值为 0 。
语言模型的好坏常用的评价指标是复杂度 perplexity 。perplexity 值刻画的就是通过某一个语言模型估计的一句话出现的概率。比如当已知(w1,w2,w3,…,Wm)这句话出现在语料库之中,那么通过语言模型计算得到这句话的概率就越高越好,也就是 perplexity 值越小越好。令 perplexity 为:
m p e r p l e x i t y ( S ) = p ( w 1 , w 2 , w 3 . . . w m ) − 1 m = 1 p ( w 1 , w 2 , w 3 . . . w m ) m = 1 ∏ i = 1 m p ( w i ∣ w 1 , w 2 . . . , w i − 1 ) m = 1 ∏ i = 1 m p ( w i ∣ w i − n + 1 , . . . , w i − 1 ) m mperplexity(S)= p(w_1,w_2,w_3 ... w_m)^{-\frac{1}{m}}=\sqrt[m]{\frac{1}{p(w_1,w_2,w_3 ... w_m)}}=\sqrt[m]{\frac{1}{\prod_{i=1}^mp(w_i|w_1,w_2 ... ,w_{i-1})}}=\sqrt[m]{\frac{1}{\prod_{i=1}^mp(w_i|w_{i-n+1}, ... ,w_{i-1})}} mperplexity(S)=p(w1,w2,w3...wm)−m1=mp(w1,w2,w3...wm)1=m∏i=1mp(wi∣w1,w2...,wi−1)1=m∏i=1mp(wi∣wi−n+1,...,wi−1)1
其中n为n-gram模型中的n。
另一种表示方式:
l o g ( p e r p l e x i t y ( s ) ) = − ∑ p ( w i ∣ w 1 , w 2 . . . w i − 1 ) m log(perplexity(s))=\frac{-\sum p(w_i|w_1,w_2...w_{i-1})}{m} log(perplexity(s))=m−∑p(wi∣w1,w2...wi−1)
相比第一种乘积开根号的表示形式,这里使用加法的形式可以加速计算,这也有效的避免了概率为0时导致整个计算结果为0的问题。
复杂度perplexity表示的是平均分支系数(average branch factor),即模型预测下一个词时的平均可选择数量。
例如:考虑一个由0-9这10个数字随机组成的长度为m的序列。由于这10个数字出现的概率是随机的,所以每个数字出现的概率是 1 10 \frac{1}{10} 101。因此在任意时刻,模型都有10个等概率的候选答案可以选择,于是perplexity的值就是10,计算过程: p e r p l e x i t y ( s ) = 1 ∏ i = 1 m 1 10 m perplexity(s)=\sqrt[m]{\frac{1}{\prod_{i=1}^m \frac{1}{10}}} perplexity(s)=m∏i=1m1011。因此有一个语言模型的perplexity是89,就表示平均情况下,模型预测下一个词时,有89个词等可能地可以作为下一个词的选择。
1.2 rnn自然语言建模
除了 n-gram 模型,RNN 也可以用来对自然语言建模,如下图所示:
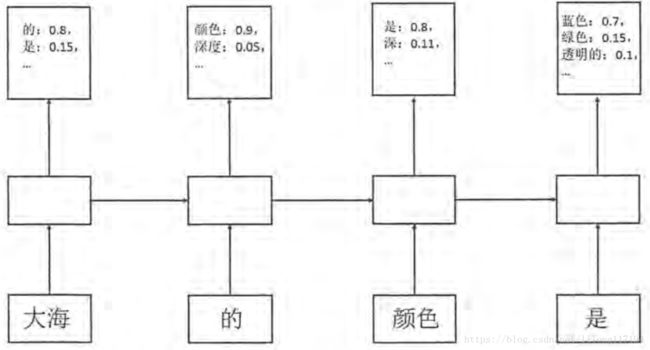
每个时刻的输入为一个句子中的单词,而每个时刻的输出为一个概率分布,表示句子中下一个位置为不同单词的概率。通过这种方式,对于给定的句子,就可以通过RNN的前向传播计算出 p ( w i ∣ w 1 , w 2 . . . w i − 1 ) p(w_i|w_1,w_2...w_{i-1}) p(wi∣w1,w2...wi−1)。
比如 “大海的颜色是蓝色” 这句话的概率,知道第一个单词是 “大海” 后,计算 p(“的”|“大海”) = 0.8,然后计算 p(x|“大海”,"的“) 、p(x|“大海”,“的”,“颜色”)、p(x|“大海”,“的”,“颜色”,“是”)。以此类推,就可以求出整句话 “大海的颜色是蓝色” 的概率。
2. 基于PTB文本数据集的自然语言模型
PTB(penn treebank dataset)文本数据集是语言模型学习中最广泛使用的数据集。下载 PTB 数据集:http://www.fit.vutbr.cz/~imikolov/rnnlm/simple-examples.tgz 解压后获取 data 目录下的三个文件:
ptb.train.txt 训练集
ptb.valid.txt 验证集
ptb.test.txt 测试集
这三个数据文件夹中的数据已经经过了预处理,包含了1000个不同的词语和语句结束标记符。TensorFlow 提供了 ptb_raw_data函数来读取PTB的数据,并将原始数据中的单词转换成单词 ID。
代码:
from tensorflow.models.tutorials.rnn.ptb import reader
DATA_PATH="PTB_data"
train_data,valid_data,test_data,_=reader.ptb_raw_data(DATA_PATH)
# 读取数据原始数据
print(len(train_data))
print(train_data[:100])
结果:
929589
[9970, 9971, 9972, 9974, 9975, 9976, 9980, 9981, 9982, 9983, 9984, 9986, 9987, 9988, 9989, 9991, 9992, 9993, 9994, 9995, 9996, 9997, 9998, 9999, 2, 9256, 1, 3, 72, 393, 33, 2133, 0, 146, 19, 6, 9207, 276, 407, 3, 2, 23, 1, 13, 141, 4, 1, 5465, 0, 3081, 1596, 96, 2, 7682, 1, 3, 72, 393, 8, 337, 141, 4, 2477, 657, 2170, 955, 24, 521, 6, 9207, 276, 4, 39, 303, 438, 3684, 2, 6, 942, 4, 3150, 496, 263, 5, 138, 6092, 4241, 6036, 30, 988, 6, 241, 760, 4, 1015, 2786, 211, 6, 96, 4]
训练数据总共包括929589个单词,而这些单词被组成了一个很长的序列。这个序列通过特殊的标识符给出了每句话结束的位置。而这个数据集中,句子结束的标识符id为2,从运行结果可以看出句子结束的位置。
构造训练集需要的batch:
import tensorflow as tf
from tensorflow.models.tutorials.rnn.ptb import reader
DATA_PATH = "PTB_data"
train_data, valid_data, test_data, _ = reader.ptb_raw_data(DATA_PATH)
print ('Total length:',len(train_data))
print (train_data[:100])
print('..........................')
tt=train_data[:100]
print(len(tt))
# 100个id分成4组,每组就是25个,截断长度为5,也就是25/5=5每组5批id,第25个id是9256
print('id:',tt[25])
"""
将训练数据组织成batch大小为4、截断长度为5的数据组。并使用队列读取前3个batch。
即是:把原始的序列从第一个算起,平均分成4组,每组的大小是平均后的长度。而截断长度是从每组中从第一个开始截取长度为5
"""
# ptb_producer返回的为一个二维的tuple数据。
result = reader.ptb_producer(tt, 4, 5)
print(type(result))
# 通过队列依次读取batch。
with tf.Session() as sess:
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(sess=sess, coord=coord)
for i in range(5):
x, y = sess.run(result)
print ("X%d: "%i, x)
print ("Y%d: "%i, y)
coord.request_stop()
coord.join(threads)
运行结果:
Total length: 929589
[9970, 9971, 9972, 9974, 9975, 9976, 9980, 9981, 9982, 9983, 9984, 9986, 9987, 9988, 9989, 9991, 9992, 9993, 9994, 9995, 9996, 9997, 9998, 9999, 2, 9256, 1, 3, 72, 393, 33, 2133, 0, 146, 19, 6, 9207, 276, 407, 3, 2, 23, 1, 13, 141, 4, 1, 5465, 0, 3081, 1596, 96, 2, 7682, 1, 3, 72, 393, 8, 337, 141, 4, 2477, 657, 2170, 955, 24, 521, 6, 9207, 276, 4, 39, 303, 438, 3684, 2, 6, 942, 4, 3150, 496, 263, 5, 138, 6092, 4241, 6036, 30, 988, 6, 241, 760, 4, 1015, 2786, 211, 6, 96, 4]
..........................
100
id: 9256
<class 'tuple'>
X0: [[9970 9971 9972 9974 9975]
[9256 1 3 72 393]
[1596 96 2 7682 1]
[3684 2 6 942 4]]
Y0: [[9971 9972 9974 9975 9976]
[ 1 3 72 393 33]
[ 96 2 7682 1 3]
[ 2 6 942 4 3150]]
X1: [[9976 9980 9981 9982 9983]
[ 33 2133 0 146 19]
[ 3 72 393 8 337]
[3150 496 263 5 138]]
Y1: [[9980 9981 9982 9983 9984]
[2133 0 146 19 6]
[ 72 393 8 337 141]
[ 496 263 5 138 6092]]
X2: [[9984 9986 9987 9988 9989]
[ 6 9207 276 407 3]
[ 141 4 2477 657 2170]
[6092 4241 6036 30 988]]
Y2: [[9986 9987 9988 9989 9991]
[9207 276 407 3 2]
[ 4 2477 657 2170 955]
[4241 6036 30 988 6]]
X3: [[9991 9992 9993 9994 9995]
[ 2 23 1 13 141]
[ 955 24 521 6 9207]
[ 6 241 760 4 1015]]
Y3: [[9992 9993 9994 9995 9996]
[ 23 1 13 141 4]
[ 24 521 6 9207 276]
[ 241 760 4 1015 2786]]
X4: [[9970 9971 9972 9974 9975]
[9256 1 3 72 393]
[1596 96 2 7682 1]
[3684 2 6 942 4]]
Y4: [[9971 9972 9974 9975 9976]
[ 1 3 72 393 33]
[ 96 2 7682 1 3]
[ 2 6 942 4 3150]]
这里主要是为了送入循环神经网络而做的数据处理。将一个长序列分成batch并截断的操作示意图如下:
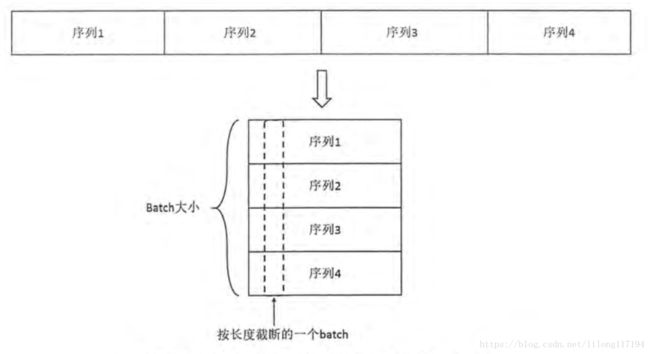
注意:
报错信息:
'AttributeError: module 'tensorflow.models.tutorials.rnn.ptb.reader' has no attribute 'ptb_iterator'
把读取 PTB 数据集的 reader的 ptb_iterator() 修改成ptb_producer()。
但还是会报错:
AttributeError: 'tuple' object has no attribute 'next',这是因为 ptb_producer() 返回的是 tuple,这时可以使用上述的方式通过建立session,使用队列来解决。
完整的RNN语言模型为:
import numpy as np
import tensorflow as tf
from tensorflow.models.tutorials.rnn.ptb import reader
DATA_PATH = "PTB_data" # 数据存储路径
HIDDEN_SIZE = 200 # 隐藏层规模
NUM_LAYERS = 2 # 深层循环网络中lstm结构的层数
VOCAB_SIZE = 10000 # 词典规模,加上语句结束标示符和稀有单词标示符,总共一万多个单词
LEARNING_RATE = 1.0 # 学习速率
TRAIN_BATCH_SIZE = 20 # 训练数据batch的大小
TRAIN_NUM_STEP = 35 # 截断长度
# 在测试时不需要使用截断,可以将测试数据看成一个超长的序列
EVAL_BATCH_SIZE = 1 # 测试数据batch的大小
EVAL_NUM_STEP = 1 # 测试数据截断的长度
NUM_EPOCH = 2 # 使用训练数据的轮数
KEEP_PROB = 0.5 # 节点不被dropout的概率
MAX_GRAD_NORM = 5 # 用于控制梯度膨胀的参数
# 通过一个PTBModel类来描述模型,这样方便维护循环神经网络中的状态
class PTBModel(object):
# 记录使用的batch的大小和截断长度
def __init__(self, is_training, batch_size, num_steps):
# 使用batch的大小和截断长度
self.batch_size = batch_size
self.num_steps = num_steps
# 定义输入层:维度为batch_size x num_steps,这和ptb_producer的函数输出的数据batch是一致的。
self.input_data = tf.placeholder(tf.int32, [batch_size, num_steps])
# 定义预期输出:它和输入是对应的,标签就是该词汇对应的下一个词汇
self.targets = tf.placeholder(tf.int32, [batch_size, num_steps])
# 定义一个基础的LSTM结构作为循环体的基础结构,深层循环神经网络也支持使用其他的循环体。
lstm_cell = tf.contrib.rnn.BasicLSTMCell(HIDDEN_SIZE)
if is_training:
# 训练时使用dropout的深层循环神经网络
lstm_cell = tf.contrib.rnn.DropoutWrapper(lstm_cell, output_keep_prob=KEEP_PROB)
# 通过MultiRNNCell类实现深层循环网络中的每一个时刻的前向传播过程
cell = tf.contrib.rnn.MultiRNNCell([lstm_cell]*NUM_LAYERS)
# 初始化最初的状态:也就是全0的向量
self.initial_state = cell.zero_state(batch_size, tf.float32)
"""
下面是tensorflow中word2vec的构建
"""
# 将单词id转换为单词向量:因为总共有VOCAB_SIZE个单词,每个单词的向量维度为hidde_size,
# 所以embedding参数的维度为10000x200
embedding = tf.get_variable("embedding", [VOCAB_SIZE, HIDDEN_SIZE])
# 将原本batch_size x numk_steps个单词ID转为单词向量,
# 转化后的输入层维度为batch_sizexnum_stepsxhidden_size
inputs = tf.nn.embedding_lookup(embedding, self.input_data)
# 只在训练时使用dropout
if is_training:
inputs = tf.nn.dropout(inputs, KEEP_PROB)
# 定义输出列表:在这里先将不同时刻的lstm结构的输出列表收集起来,再通过一个全连接层得到最终的输出
outputs = []
# state存储不同batch中lstm的“状态”,将其初始化为0
state = self.initial_state
with tf.variable_scope("RNN"):
# 这里num_steps是截断长度为35:为了避免梯度消散问题,会规定一个最大的序列长度,就是num_steps
for time_step in range(num_steps):
# 在第一个时刻需要声明网络中的变量,在之后的时刻都需要复用之前定义好的变量。
if time_step > 0: tf.get_variable_scope().reuse_variables()
# 每一步处理时间序列中的一个时刻。将当前的输入和前一时刻状态传入定义好的网络结构,
# 可以得到当前的输出和更新的状态
cell_output, state = cell(inputs[:, time_step, :], state)
# 将当前输出加入到输出队列
outputs.append(cell_output)
# 把输出队列展开成[batch,hidden_size*num_steps]的形状,然后再reshape成[batch*num_steps,hidden_size]的形状
# tf.concat(concat_dim, values, name='concat'),这里完全是为了后面全连接层的运算(3D化为2D)
output = tf.reshape(tf.concat(outputs, 1), [-1, HIDDEN_SIZE])
# 将从lstm中得到的输出再经过一个全连接层得到最后的预测结果,
# 最终的预测结果在每一个时刻上都是一个长度为vocab_size的数组,经过softamx层之后表示下一个位置是不同单词的概率
weight = tf.get_variable("weight", [HIDDEN_SIZE, VOCAB_SIZE])
bias = tf.get_variable("bias", [VOCAB_SIZE])
logits = tf.matmul(output, weight) + bias # [20x35,200]*[200x10000]+[10000]
# 定义交叉熵损失函数:tf使用sequence_loss_by_example函数来计算一个序列的交叉熵的和
loss = tf.contrib.legacy_seq2seq.sequence_loss_by_example(
[logits], # 预测的结果
[tf.reshape(self.targets, [-1])], # 期望的正确答案,这里将[batch,num_step]的二维数组压缩成一维数组
# 损失的权重:这里所有的权重都为1,也就是说不同batch和不同时刻的重要程度是一样的
[tf.ones([batch_size * num_steps], dtype=tf.float32)])
# 计算得到每个batch的平均损失
self.cost = tf.reduce_sum(loss) / batch_size
self.final_state = state
# 只在训练模型时定义反向传播操作。
if not is_training: return
trainable_variables = tf.trainable_variables()
# 通过clip_by_global_norm函数控制梯度大小,避免梯度膨胀的问题。
grads, _ = tf.clip_by_global_norm(tf.gradients(self.cost, trainable_variables), MAX_GRAD_NORM)
# 定义优化方法
optimizer = tf.train.GradientDescentOptimizer(LEARNING_RATE)
# 定义训练步骤
self.train_op = optimizer.apply_gradients(zip(grads, trainable_variables))
# 使用给定的模型model在数据data上运行train_op并返回在全部数据上的perolexity值
def run_epoch(session, model, data, train_op, output_log, epoch_size):
# 计算perplexity的辅助变量
total_costs = 0.0
iters = 0
state = session.run(model.initial_state)
# 使用当前数据训练或者测试模型
for step in range(epoch_size):
x, y = session.run(data)
# 在当前batch上运行train_op并计算损失值,交叉熵损失函数计算的就是下一个单词为给定单词的概率
cost, state, _ = session.run(
[model.cost, model.final_state, train_op],
{model.input_data: x, model.targets: y,
model.initial_state: state})
# 将不同时刻、不同batch的概率加起来再将这个和做指数运算就可以得到perplexity值(公式二)
total_costs += cost
iters += model.num_steps
# 只有在训练时输出日志
if output_log and step % 100 == 0:
print("After %d steps, perplexity is %.3f" % (step, np.exp(total_costs / iters)))
# 返回给定模型在给定数据上的perplexity值
return np.exp(total_costs / iters)
def main():
# 获得原始数据
train_data, valid_data, test_data, _ = reader.ptb_raw_data(DATA_PATH)
print ('length of traindata:',len(train_data))
# 计算一个epoch需要训练的次数
train_data_len = len(train_data)
# 这里的‘//’是取整的意思
train_batch_len = train_data_len // TRAIN_BATCH_SIZE
# 这里得到的是每个batch可以分成多少个step
train_epoch_size = (train_batch_len - 1) // TRAIN_NUM_STEP
print('train_epoch_size:',train_epoch_size)
# 同上
valid_data_len = len(valid_data)
valid_batch_len = valid_data_len // EVAL_BATCH_SIZE
valid_epoch_size = (valid_batch_len - 1) // EVAL_NUM_STEP
print('valid_epoch_size:',valid_epoch_size)
# 同上
test_data_len = len(test_data)
test_batch_len = test_data_len // EVAL_BATCH_SIZE
test_epoch_size = (test_batch_len - 1) // EVAL_NUM_STEP
print('test_epoch_size:',test_epoch_size)
# 定义初始化函数
initializer = tf.random_uniform_initializer(-0.05, 0.05)
# 定义训练用的循环神经网络模型
with tf.variable_scope("language_model", reuse=None, initializer=initializer):
train_model = PTBModel(True, TRAIN_BATCH_SIZE, TRAIN_NUM_STEP)
# 定义测试用的循环神经网络模型
with tf.variable_scope("language_model", reuse=True, initializer=initializer):
eval_model = PTBModel(False, EVAL_BATCH_SIZE, EVAL_NUM_STEP)
# 训练模型。
with tf.Session() as session:
tf.global_variables_initializer().run()
train_queue = reader.ptb_producer(train_data, train_model.batch_size, train_model.num_steps)
eval_queue = reader.ptb_producer(valid_data, eval_model.batch_size, eval_model.num_steps)
test_queue = reader.ptb_producer(test_data, eval_model.batch_size, eval_model.num_steps)
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(sess=session, coord=coord)
# 使用训练数据训练模型
for i in range(NUM_EPOCH):
print("In iteration: %d" % (i + 1))
# 在所有的训练数据上训练循环神经网络
run_epoch(session, train_model, train_queue, train_model.train_op, True, train_epoch_size)
# 使用验证数据集评测数据效果
valid_perplexity = run_epoch(session, eval_model, eval_queue, tf.no_op(), False, valid_epoch_size)
print("Epoch: %d Validation Perplexity: %.3f" % (i + 1, valid_perplexity))
# 使用测试数据集测试模型效果
test_perplexity = run_epoch(session, eval_model, test_queue, tf.no_op(), False, test_epoch_size)
print("Test Perplexity: %.3f" % test_perplexity)
coord.request_stop()
coord.join(threads)
"""
主函数入口
"""
if __name__ == "__main__":
main()
运行结果:
length of traindata: 929589
train_epoch_size: 1327
valid_epoch_size: 73759
test_epoch_size: 82429
In iteration: 1
After 0 steps, perplexity is 9980.495
After 100 steps, perplexity is 1389.408
After 200 steps, perplexity is 1021.756
After 300 steps, perplexity is 853.102
After 400 steps, perplexity is 746.115
After 500 steps, perplexity is 673.331
After 600 steps, perplexity is 621.486
After 700 steps, perplexity is 577.891
After 800 steps, perplexity is 538.988
After 900 steps, perplexity is 508.633
After 1000 steps, perplexity is 485.270
After 1100 steps, perplexity is 462.591
After 1200 steps, perplexity is 443.829
After 1300 steps, perplexity is 426.913
Epoch: 1 Validation Perplexity: 244.784
In iteration: 2
After 0 steps, perplexity is 370.560
After 100 steps, perplexity is 259.848
After 200 steps, perplexity is 264.565
After 300 steps, perplexity is 265.816
After 400 steps, perplexity is 263.193
After 500 steps, perplexity is 260.594
After 600 steps, perplexity is 260.226
After 700 steps, perplexity is 257.938
After 800 steps, perplexity is 253.309
After 900 steps, perplexity is 250.747
After 1000 steps, perplexity is 249.277
After 1100 steps, perplexity is 246.004
After 1200 steps, perplexity is 243.725
After 1300 steps, perplexity is 241.052
Epoch: 2 Validation Perplexity: 198.344
Test Perplexity: 191.840
通过输出可以看出,在迭代开始时perplexity值为9980.495,这也就是说相当于从10000个单词中随机选择下一个单词,而在训练结束后,perplexity的值降低到了 ,这说明通过训练将选择下一个单词的范围从10000个减少到大约190,当然还可以通过修改参数,把perplexity降低到更低。