HashMap与LinkedHashMap

http://www.admin10000.com/document/3322.html
刚看完,赶紧记录一下, 看看是否能把知识梳理一哈;
关于装填因子的取值以及扩容的问题, 我打算放在最后面讲;

1.HashMap():

1. 构造函数
2. put(K key,V value);
3. get(K key);

1、构造函数:

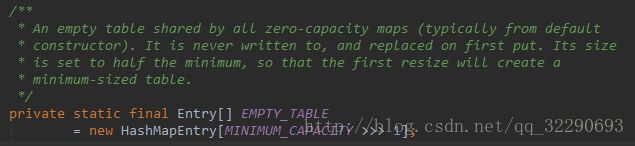
1. HashMap();
2. HashMap(int capacity);
3. HashMap(int capacity, float factor);
4. HashMap(Map extends K, ? extends V> map);

关于这四个构造方法, 本质区别就是在于初创的数组的大小, 默认数组的大小为2;

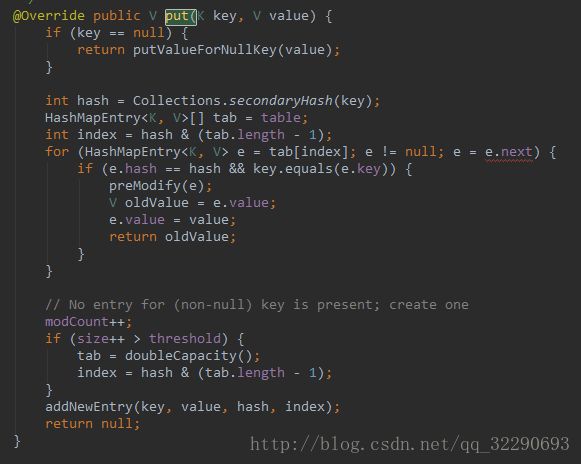
2、put(K key, V value)

key == null时

这个操作也说明了HashMap是允许插入key = null值的.
如果HashMap中没有进行过插入key = null的操作, 则新加入null-value的键值对, 如果已经插入过null-value的键值对, 则将新value替换就value. 然后这里有一个preModify(entry)方法. 我们切进去看看.

这个就6了, 是个空方法, 在LinkedHashMap的时候儿才会被具体实现.

然后我们切回到put(K key, V value)方法:

当key!=null时, 求hash值得方法目前先不看了, 他就是采用了一个比较好的方法, 能保证关键字都能比较均匀的散列在Hash桶中.

上图中知道HashMap内部其实是一个数组, 也称为Hash桶.
数组中每个元素的索引是通过hash&[tab.length -1]计算的出来的;
正因为他的内部是一个数组结构, 所以默认情况下HashMap进行一次查找的时间复杂度为O[1].
然后我们关注一波接下来的for循环.

for (HashMapEntry e = tab[index]; e != null; e = e.next) {
    if (e.hash == hash && key.equals(e.key)) {
        preModify(e);
        V oldValue = e.value;
        e.value = value;
        return oldValue;
    }
}

上面操作叫作hash碰撞, 即当新插入的元素和桶中某个元素的key值相同是, 就会进行value的替换, 并且也仅仅是进行了替换操作.

如果遍历对应于index上的链表的所有元素, 也没有发现该key-value,则继续向下走,执行addNewEntry()方法:

注意重点在于this.next = next, 而next = table[index], 如果index位置有元素, 则新插入的元素前驱于旧元素. 这个操作也说明了Hash桶中每个位置都是放了一个表, 而该表的结构是单链表.

注意一点, 每次插入元素都是this.next = next , 每次插入元素都是在链表的最前端进行的插入.

HashMap分析起来要简单一些. 接下来看看他的get()方法.

我们还是重点关注for循环, 从循环条件可以看出, 他是从表头开始遍历. 讨论最坏的情况下, 假设哈希桶中所有元素个数n, 地址个数为m, 装填因子为K该桶的所有元素都集中在这一条链表上, 则查找的平均时间复杂度为n/(m*k).

现在市面上很多关于DiskLruCache的博客讲到最近查找算法时都是一带而过, 最近插入的元素很可能在短期内被使用, DiskLruCache就是用到了HashMap的这一点特征, 插入元素时将最新插入的元素放在链表的第一位, 所以在进行查找时, 如果最新插入的元素再次被查找时, 就能保证时间复杂度最低.

但是DiskLruCache的插入, 查找方法还是和HashMap有点儿区别, 他内部维护的是LinkedHashMap结构.

有一点还是没讲, 为什么扩容时, 是double * capacity的方式进行的扩容, 这个放在最后面讲, 他是一道数学证明题.

接下来看看LinkedHashMap和HashMap的区别在哪里:

2.LinkedHashMap:

1. 构造函数;
2. put();
3. get();

1、构造函数:

1. LinkedHashMap();
2. LinkedHashMap(int capacity);
3. LinkedHashMap(int capacity, float factor);
4. LinkedHashMap(int initialCapacity, float loadFactor, boolean accessOrder);

关注一波第四个函数

@Override void init() {
    header = new LinkedEntry();
}

除了init()方法其他仅仅是进行了赋值, 没有进行其他的操作.

然后我们关注一波put()方法, 我们发现LinkedHashMap中并没有出现put()方法, 查看源码知道他只是对其中几个关键的点进行了重写,
重写HashMap的方法有:

1. preModify();
2. addNewEntry();

也就是对于put()方法, 我们要重点关注一波这两个方法, 看看他与HashMap的插入方法到底有何区别.

先看看preMofify()方法:

看到这里, 只有当accessOrder才会进入到makeTail里面去, 如果我们平时使用LinkedHashMap时一般习惯性是这样的

LinkedHashMap map = new LinkedHashMap();

这样, 在遇到冲突时, 他的默认是和HashMap一样, 仅仅进行了替换操作. 然后这里我先猜想, DiskLruCache肯定是调用了第四个构造函数

LinkedHashMap(int initialCapacity, float loadFactor, boolean accessOrder);

然后我们去DiskLruCache里面大致的看一下.

我这里打开的是Glide里面的DiskLruCache源码. 这里不做追究, 具体如何缓存肯定是研究Glide源码的一个关键点.

假如设置accessOrder为true.

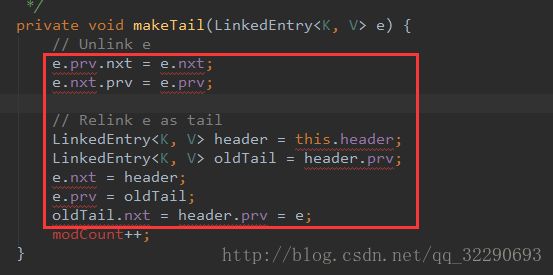
如果能够成功进入makeTail()方法, 其实也表明HashMap中已经插入过Key-oldValue键值对, 他这里进行的操作是先把Key所在的结点从该链表中删除, 然后再将删除的结点前驱于header,后继于oldTail;
如果是新手入门, 是从这段代码看出来的.

将该元素插入到tailOld与header之间, 同时这段代码也说明了hash桶的每条链表都是一个双链表结构.

接下来切入到addNewEntry().

关键点还是在于最后一句, 把最近插入的元素插入到链表的表头, 这样在遍历链表, 如果要获取最新插入的元素, 时间复杂度仅仅为0[1];

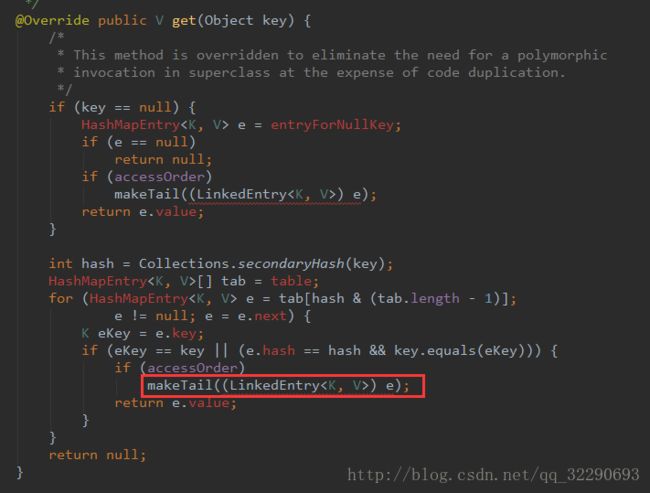
put()方法告一段落, 接下来是get()方法:

注意, 当accessOrder为true时, get方法也走到了makeTail中, 当我们获取某个元素时, 先将它插入到tail与header中间, 然后再进行获取值, 一个原因就是我们获取一个值, 那么我们很可能在短期内继续获取这个值, 这样可以保证他的时间复杂度最低;

HashMap与LinkedHashMap的三个最基本的方法分析完了, 其实感觉分析的也是很皮毛, 仅仅是把流程走了一遍.

现在我们来看看扩容操作.
在进行插入操作时, 如果发现桶中容量即将装满, 就是会调用doubleCapacity()方法, 我们切进去看看具体实现:

这里我们只关注int newCapacity = oldCapacity*2; 后面的部分主要是将关键字均匀的散列在固定大小的hash桶中. 关于如何实现, 我现在还没有能力讲, 等我把散列相关的数据结构和算法看完再继续这部分, 这里先个任务;

当容量满了以后为什么是2倍的形式去扩容而不是1倍或者3倍.

假设扩容倍数是1, 假设初始容量为T, 我们最终的元素为n = m*T,也就是进行了m次扩容. 那么每次扩容, 我们都要进行数组拷贝, 那么总的时间复杂度为
O(n) = (1 + 2 + 3 + …. + m) *T = m(m-1)T/2 = (m-1)n/2.
进行了m次扩容, 平均每次扩容的时间复杂度为 O(N).

如果我们选择扩容因子为2.
假设插入的元素 n = 2^m, 那么扩容进行数组拷贝之和为
O(n) = 2^0 + 2^1 + … + 2^m = (2^m-1) = n,
则平均每次扩容进行数组拷贝的时间复杂度为O(1).
依次类推, 扩容因子为3,4,5…时间复杂度都是O(1), 但是扩容因子选取过大以后, 他的空间复杂度就会变得很大.

分析到这里也就分析完了, 这次终于在没有借助别人的博客的基础上自己搞定一篇博客;

其中有一些细节留待看完数据结构和算法以后再来深究.