几种循环神经网络RNN，Bidirectional RNN，LSTM，GRU

背景

前馈网络、CNN对序列数据只能采用固定长度作为输入，但是，句子、音频等数据，输入固定长度（虽然可以通过输入填充到固定大小来克服）。这两种网络仍比序列模型RNN表现更差，因为传统模型不理解输入的上下文。

1 循环神经网络Recurrent Neural Network

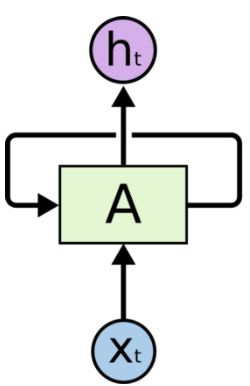
循环神经网络，时间步的每个节点从前前一个节点获取输入，并不断反馈循环。

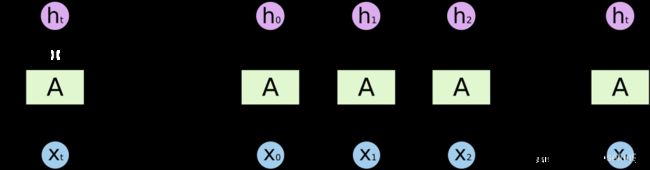
表示形式：
$$\begin{gathered} {\mathbf{a}}_t=f({\mathbf{h}}_{t-1},{\mathbf{x}}_t), \\ \mathbf{g}(\mathbf{x})=tanh\mathbf{x}, \\ {\mathbf{a}}_t=g({\mathbf{W}}_{hh}\cdot {\mathbf{h}}_{t-1}+{\mathbf{W}}_{xh}\cdot {\mathbf{x}}_t) \\ {\mathbf{h}}_t={\mathbf{W}}_{hy}\cdot {\mathbf{a}}_t \end{gathered}$$

2. 长短时神经网络LSTM

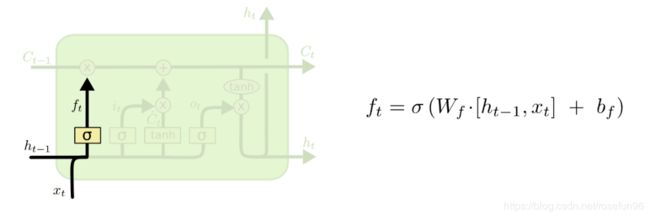
2.1 遗忘门

$f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$

2.2 更新门

$i_t$ 是输入门结果；${\hat{C}}_t$为当前输入的细胞状态，未考虑上一时刻细胞状态.

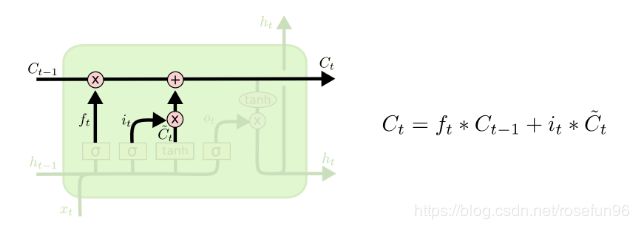
$C_t$ 为更新后当前时刻的细胞状态，一部分由前一时刻细胞状态，加上当前时刻的细胞状态，这两部分都考虑到了上一时刻的隐层状态$h_{t-1}$。

疑惑：这里为什么使用 tanh 激活函数？ 更新门就是，tanh 激活函数和 sigmoid 激活函数后的矩阵逐位相乘。

LSTM管理一个内部状态向量，当我们添加某个函数的输出时，其值应该能够增加或减少。 Sigmoid输出总是非负的;该州的价值只会增加。 tanh的输出可以是正的或负的，允许状态的增加和减少。

2.3 输出门

当前时刻输出为 $o_t$, 与前一时刻学习到的信息$h_{t-1}$和 当前时刻信息$x_t$ 有关。
输出$o_t$和经过tanh变换的细胞状态$C_t$，作为 当前时刻的信息$h_t$.
包含细胞状态的都用$tanh$激活函数。

3 门控循环单元GRU

GRU比LSTM训练时间更加短，同时也可以记住长期依赖。

$z_t$代表更新门操作；$r_t$代表重置门操作, $h_t$代表 t 时刻隐层信息。

GRU只有更新门$z_t$ 和重置门$r_t$，没有输出门和细胞状态。
更新门决定有多少过去信息用来利用，重置门决定多少过去信息丢弃。
思想就是充分考虑前一时刻隐层状态信息$h_{t-1}$,和当前时刻的信息${\hat{h}}_t$,这两部分通过权重$z_t$来调节。

一般来说，GRU计算快速，计算精度略低于LSTM。

4 双向RNN

双向RNN的出发点是，有时模型需要读取序列数据的上下文来消除歧义，特别是在文本领域。
双向RNN的重复模块是传统RNN，LSTM或者GRU单元，并且有一种在时间上前向学习过程和向后学习过程。

5. 实践

简单模拟RNN实现，

import copy, numpy as np
np.random.seed(0)

# compute sigmoid nonlinearity
def sigmoid(x):
    output = 1/(1+np.exp(-x))
    return output

# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
    return output*(1-output)


# training dataset generation
int2binary = {}
binary_dim = 8

largest_number = pow(2,binary_dim)
binary = np.unpackbits(
    np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
for i in range(largest_number):
    int2binary[i] = binary[i]


# input variables
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1


# initialize neural network weights
synapse_0 = 2*np.random.random((input_dim,hidden_dim)) - 1
synapse_1 = 2*np.random.random((hidden_dim,output_dim)) - 1
synapse_h = 2*np.random.random((hidden_dim,hidden_dim)) - 1

synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)

# training logic
for j in range(10000):
    
    # generate a simple addition problem (a + b = c)
    a_int = np.random.randint(largest_number/2) # int version
    a = int2binary[a_int] # binary encoding

    b_int = np.random.randint(largest_number/2) # int version
    b = int2binary[b_int] # binary encoding

    # true answer
    c_int = a_int + b_int
    c = int2binary[c_int]
    
    # where we'll store our best guess (binary encoded)
    d = np.zeros_like(c)

    overallError = 0
    
    layer_2_deltas = list()
    layer_1_values = list()
    layer_1_values.append(np.zeros(hidden_dim))
    
    # moving along the positions in the binary encoding
    for position in range(binary_dim):
        
        # generate input and output
        X = np.array([[a[binary_dim - position - 1],b[binary_dim - position - 1]]])
        y = np.array([c[binary_dim - position - 1]]).T

        # hidden layer (input ~+ prev_hidden)
        layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h))

        # output layer (new binary representation)
        layer_2 = sigmoid(np.dot(layer_1,synapse_1))

        # did we miss?... if so, by how much?
        layer_2_error = y - layer_2
        layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2))
        overallError += np.abs(layer_2_error[0])
    
        # decode estimate so we can print it out
        d[binary_dim - position - 1] = np.round(layer_2[0][0])
        
        # store hidden layer so we can use it in the next timestep
        layer_1_values.append(copy.deepcopy(layer_1))
    
    future_layer_1_delta = np.zeros(hidden_dim)
    
    for position in range(binary_dim):
        
        X = np.array([[a[position],b[position]]])
        layer_1 = layer_1_values[-position-1]
        prev_layer_1 = layer_1_values[-position-2]
        
        # error at output layer
        layer_2_delta = layer_2_deltas[-position-1]
        # error at hidden layer
        layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(synapse_1.T)) * sigmoid_output_to_derivative(layer_1)

        # let's update all our weights so we can try again
        synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
        synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
        synapse_0_update += X.T.dot(layer_1_delta)
        
        future_layer_1_delta = layer_1_delta
    

    synapse_0 += synapse_0_update * alpha
    synapse_1 += synapse_1_update * alpha
    synapse_h += synapse_h_update * alpha    

    synapse_0_update *= 0
    synapse_1_update *= 0
    synapse_h_update *= 0
    
    # print out progress
    if(j % 1000 == 0):
        print("Error:" + str(overallError)) 
        print ("Pred:" + str(d))
        print ("True:" + str(c))
        out = 0
        for index,x in enumerate(reversed(d)):
            out += x*pow(2,index)
        print (str(a_int) + " + " + str(b_int) + " = " + str(out))
        print ("------------")

Example 2 搭建RNN：

# coding: utf-8

import numpy as np
import tensorflow as tf
from tensorflow.python import debug as tf_debug
from matplotlib import pyplot as plt

'''超参数'''
num_steps = 10
batch_size = 200
num_classes = 2
state_size = 16
learning_rate = 0.1

'''生成数据
就是按照文章中提到的规则，这里生成1000000个
'''
def gen_data(size=1000000):
    X = np.array(np.random.choice(2, size=(size,)))
    Y = []
    '''根据规则生成Y'''
    for i in range(size):   
        threshold = 0.5
        if X[i-3] == 1:
            threshold += 0.5
        if X[i-8] == 1:
            threshold -=0.25
        if np.random.rand() > threshold:
            Y.append(0)
        else:
            Y.append(1)
    return X, np.array(Y)


'''生成batch数据'''
def gen_batch(raw_data, batch_size, num_step):
    raw_x, raw_y = raw_data
    data_length = len(raw_x)
    batch_patition_length = data_length // batch_size                         # ->5000
    data_x = np.zeros([batch_size, batch_patition_length], dtype=np.int32)    # ->(200, 5000)
    data_y = np.zeros([batch_size, batch_patition_length], dtype=np.int32)    # ->(200, 5000)
    '''填到矩阵的对应位置'''
    for i in range(batch_size):
        data_x[i] = raw_x[batch_patition_length*i:batch_patition_length*(i+1)]# 每一行取batch_patition_length个数，即5000
        data_y[i] = raw_y[batch_patition_length*i:batch_patition_length*(i+1)]
    epoch_size = batch_patition_length // num_steps                           # ->5000/5=1000 就是每一轮的大小
    for i in range(epoch_size):   # 抽取 epoch_size 个数据
        x = data_x[:, i * num_steps:(i + 1) * num_steps]                      # ->(200, 5)
        y = data_y[:, i * num_steps:(i + 1) * num_steps]
        yield (x, y)    # yield 是生成器，生成器函数在生成值后会自动挂起并暂停他们的执行和状态（最后就是for循环结束后的结果，共有1000个(x, y)）
def gen_epochs(n, num_steps):
    for i in range(n):
        yield gen_batch(gen_data(), batch_size, num_steps)

'''定义placeholder'''
x = tf.placeholder(tf.int32, [batch_size, num_steps], name="x")
y = tf.placeholder(tf.int32, [batch_size, num_steps], name='y')
init_state = tf.zeros([batch_size, state_size])
'''RNN输入'''
x_one_hot = tf.one_hot(x, num_classes)
rnn_inputs = tf.unstack(x_one_hot, axis=1)

'''定义RNN cell'''
with tf.variable_scope('rnn_cell'):
    W = tf.get_variable('W', [num_classes + state_size, state_size])
    b = tf.get_variable('b', [state_size], initializer=tf.constant_initializer(0.0))
    
def rnn_cell(rnn_input, state):
    with tf.variable_scope('rnn_cell', reuse=True):
        W = tf.get_variable('W', [num_classes+state_size, state_size])
        b = tf.get_variable('b', [state_size], initializer=tf.constant_initializer(0.0))
    return tf.tanh(tf.matmul(tf.concat([rnn_input, state],1),W) + b)
'''将rnn cell添加到计算图中'''
state = init_state
rnn_outputs = []
for rnn_input in rnn_inputs:
    state = rnn_cell(rnn_input, state)  # state会重复使用，循环
    rnn_outputs.append(state)
final_state = rnn_outputs[-1]        # 得到最后的state

#cell = tf.contrib.rnn.BasicRNNCell(num_units=state_size)
#rnn_outputs, final_state = tf.contrib.rnn.static_rnn(cell=cell, inputs=rnn_inputs, 
                                                    #initial_state=init_state)
#rnn_outputs, final_state = tf.nn.dynamic_rnn(cell=cell, inputs=rnn_inputs, 
                                                    #initial_state=init_state)


'''预测，损失，优化'''
with tf.variable_scope('softmax'):
    W = tf.get_variable('W', [state_size, num_classes])
    b = tf.get_variable('b', [num_classes], initializer=tf.constant_initializer(0.0))
logits = [tf.matmul(rnn_output, W) + b for rnn_output in rnn_outputs]
predictions = [tf.nn.softmax(logit) for logit in logits]

y_as_list = tf.unstack(y, num=num_steps, axis=1)
losses = [tf.nn.sparse_softmax_cross_entropy_with_logits(labels=label,logits=logit) for logit, label in zip(logits, y_as_list)]
total_loss = tf.reduce_mean(losses)
train_step = tf.train.AdagradOptimizer(learning_rate).minimize(total_loss)


'''训练网络'''
def train_rnn(num_epochs, num_steps, state_size=4, verbose=True):
    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        #sess = tf_debug.LocalCLIDebugWrapperSession(sess)
        training_losses = []
        for idx, epoch in enumerate(gen_epochs(num_epochs, num_steps)):
            training_loss = 0
            training_state = np.zeros((batch_size, state_size))   # ->(200, 4)
            if verbose:
                print('\nepoch', idx)
            for step, (X, Y) in enumerate(epoch):
                tr_losses, training_loss_, training_state, _ = \
                    sess.run([losses, total_loss, final_state, train_step], feed_dict={x:X, y:Y, init_state:training_state})
                training_loss += training_loss_
                if step % 100 == 0 and step > 0:
                    if verbose:
                        print('第 {0} 步的平均损失 {1}'.format(step, training_loss/100))
                    training_losses.append(training_loss/100)
                    training_loss = 0
    return training_losses

training_losses = train_rnn(num_epochs=5, num_steps=num_steps, state_size=state_size)
print(training_losses[0])
plt.plot(training_losses)
plt.show()

总结

双向LSTM模型一般具有较高的性能。

---

reference：

1. towards 几种RNN讲解；
2. blog rnn讲解;
3. 徒手写递归神经网络;
4. RNN-LSTM循环神经网络-Tensorflow实现；
5. lstm 使用 tanh 激活函数原因；
6. Understanding LSTM from the code;