目录
- 常见的概率分布模型
- 一、离散概率分布函数
- 二、连续概率分布函数
- 三、联合分布函数
- 四、多项分布(Multinomial Distribution)
- 4.1 多项分布简介
- 4.2 多项分布公式解析
- 五、伯努利分布(Bernoulli Distribution)
- 5.1 伯努利分布简介
- 5.2 伯努利分布的期望值和方差
- 六、正态(高斯)分布(Normal(Gaussian) Distribution)
- 6.1 正态分布的概率密度函数图像
- 6.2 正态分布简介
- 6.3 中心极限定理与正态分布
- 七、泊松分布(Poisson Distribution)
- 7.1 泊松分布的概率质量函数图像
- 八、二项分布(Binomial Distributio)
- 8.1 二项分布的概率质量函数图像
- 8.2 二项分布简介
- 8.3 二项分布与伯努利分布
- 九、贝塔分布(Beta Distribution)
- 9.1 贝塔分布的概率密度函数图像
- 十、几何分布(负二项分布)(Geometric Distribution)
- 10.1 几何分布概率质量函数图像
- 十一、狄利克雷分布(多项分布的共轭分布)(Dirichlet distribution)
- 十二、超几何分布(Hypergeometric Distribution)
- 十三、指数分布(Exponential Distribution)
- 13.1 指数分布概率密度函数图像
更新、更全的《机器学习》的更新网站,更有python、go、数据结构与算法、爬虫、人工智能教学等着你:https://www.cnblogs.com/nickchen121/p/11686958.html
常见的概率分布模型
一、离散概率分布函数
离散概率分布也称为概率质量函数(probability mass function),离散概率分布的例子有
伯努利分布(Bernoulli distribution)
二项分布(binomial distribution)
泊松分布(Poisson distribution)
几何分布(geometric distribution)等
二、连续概率分布函数
连续概率分布也称为概率密度函数(probability density function),它们是具有连续取值(例如一条实线上的值)的函数,连续概率分布的例子有
正态分布(normal distribution)
指数分布(exponential distribution)
β分布(beta distribution)等
三、联合分布函数
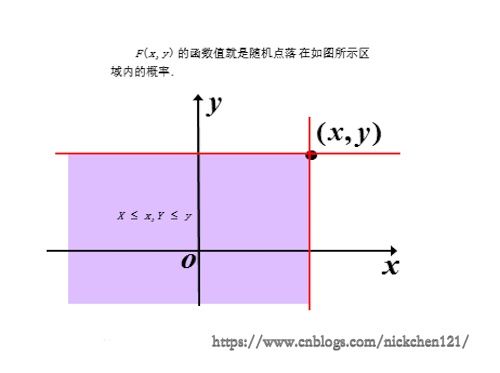
给定一个随机变量\((X,Y)\),称定义域为整个平面的二元实值函数
\[ F(x,y) = P(X\leq{x},Y\leq{y}) \quad -\infty\geq{x,y}\leq\infty \]
该二元实值函数为随机变量\((X,Y)\)的分布函数,也可以称为是\((X,Y)\)的联合分布函数。
按照联合分布函数的定义,\(F(x,y)=P((X,Y)\in{D_{xy}})\),其中\(D_{xy}\)如下图所示
四、多项分布(Multinomial Distribution)
4.1 多项分布简介
多项分布是二项分布的推广,他们的区别是二项分布的结果只有\(0\)和\(1\)两种,多项式的结果可以有多个值。
多项分布的典型例子是掷骰子,6个点对应6个不同的数,每个点的概率都为\({\frac{1}{6}}\)
与二项分布类似,多项分布来自于\((p_1+p_2+\cdots+p_k)^n多项式的展开\)
4.2 多项分布公式解析
以掷骰子为例,掷骰子的时候掷\(1-6\)的概率都为\({\frac{1}{6}}\),记作\(p_1-p_6\),可以发现\(p_1+p_2+p_3+p_4+p_5+p_6=1\),现在把\(p_1+p_2+p_3+p_4+p_5+p_6\)记作做一次抽样各种事件发生的概率和,即可得\((p_1+p_2+p_3+p_4+p_5+p_6)^n=1^n\)为\(n\)次抽样所有事件相互组合对应的概率和,之后使用多项式展开(注:使用多项式定理展开,由于多项式定理不在本节提及范围内,不多赘述),如果它不是掷骰子,而是一个有\(n\)种可能的问题,会得到一个多项式展开的公式
\[ P(X_1 = x_1,\ldots,X_k = x_k) = \begin{cases} {\frac{n!}{x_1!\cdots{x_k!}}}(p^{x_1}\cdots{p^{x_k})} \quad when\sum_{i=1}^kx_i=n\\ 0 \quad otherwise \\ \end{cases} \]
这个多项式表示\(X_1\)出现\(x_1\)次,\(X_2\)出现\(x_2\)次,\(\ldots\),\(X_k\)出现\(x_k\)次的出现概率,这样就得到了上述所示的多项分布的多项展开式公式。
五、伯努利分布(Bernoulli Distribution)
5.1 伯努利分布简介
伯努利分布是一个二值离散分布,结果只有\(0\)和\(1\)两种。
随即变量\(X\)为\(1\)的概率为\(p\),则为\(0\)的概率为\(q=1-p\),可以用公式表示为
\[ f(x) = p^x(1-p)^{1-x} = \begin{cases} p, \quad\quad x=1 \\ 1-p, \quad x=0 \\ \end{cases} \]
5.2 伯努利分布的期望值和方差
伯努利分布的期望值为
\[ \begin{align} E(X) & = \sum_{i=0}^1x_if(x) \\ & = 1*p+0*(1-p) \\ & = p+0 \\ & = p \\ \end{align} \]
伯努利分布的方差为
\[ \begin{align} D(x) & = \sum_{i=0}^1(x_i - E(x))^2f(x) \\ & = (1-E(x))^2*p + (0-E(x)^2*(1-p) \\ & = (1-p)^2*p + (0-p)^2*(1-p) \\ & = p - p^2 \\ & = p(1-p) \\ & = pq \end{align} \]
六、正态(高斯)分布(Normal(Gaussian) Distribution)
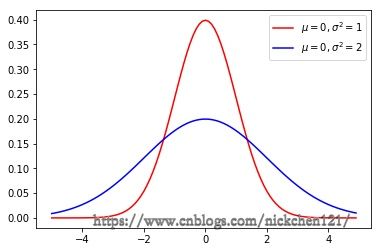
6.1 正态分布的概率密度函数图像
其中红线表示的是标准正态分布图像。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
mu1 = 0
sig1 = 1
mu2 = 0
sig2 = 2
x = np.arange(-5, 5, 0.1)
y1 = stats.norm.pdf(x, mu1, sig1)
y2 = stats.norm.pdf(x, mu2, sig2)
plt.plot(x, y1, 'r-', label='$\mu=0,\sigma^2=1$')
plt.plot(x, y2, 'b-', label='$\mu=0,\sigma^2=2$')
plt.legend()
plt.show()6.2 正态分布简介
正态分布也称作高斯分布,是最常见的一种分布,其概率密度函数为
\[ f(x;\mu,\sigma) = {\frac {1} {\sqrt{2\pi\sigma^2}} } e^{(-{\frac {(x - \mu)^2} {2\sigma^2}})} \]
如果一个随即变量\(X\)服从该分布,可以写作\(X ~ { N(\mu ,\sigma ^{2})} N(\mu, \sigma^2)\)。
当\(\mu=0,\sigma=1\)时的正态分布称作标准正态分布,这个分布能简化为
\[ f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right) \]
标准正态分布曲线区间面积计算
\[ f(|x-\mu|<\sigma) = 0.6826 \\ f(|x-\mu|<2\sigma) = 0.9544 \\ f(|x-\mu|<3\sigma) = 0.9974 \\ \]
6.3 中心极限定理与正态分布
- 中心极限定理1:把许多未知的小作用加起来看作一个变量,这个变量服从正态分布
- 中心极限定理2:“大量统计独立的随即变量的和”的分布趋于正态分布
七、泊松分布(Poisson Distribution)
7.1 泊松分布的概率质量函数图像
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
lambd = 2.5
x = np.arange(0, 10)
y = stats.poisson.pmf(x, lambd)
plt.plot(x, y, label='$\lambda=2.5$')
plt.legend()
plt.show()八、二项分布(Binomial Distributio)
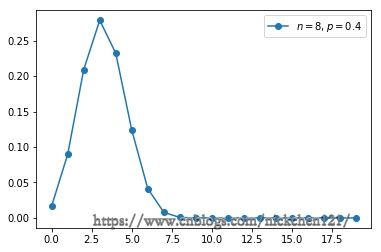
8.1 二项分布的概率质量函数图像
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
n = 8
p = 0.4
x = np.arange(0, 20)
y = stats.binom.pmf(x, n, p)
plt.plot(x, y, 'o-', label='$n=8,p=0.4$')
plt.legend()
plt.show()8.2 二项分布简介
二项分布是\(n\)次独立的二值实验(伯努利实验)中成功的次数的离散值概率分布(\(n\)次伯努利实验,一次伯努利实验得到一个伯努利分布)。
随机变量\(X\)服从参数\(n\)和\(p\)的二项分布记作:\(B(n,p)\)。\(n\)次实验中\(k\)次成功的概率质量函数为
\[ f(k;n,p) = C_n^kp^k(1-p)^{n-k} \]
其中\(C_n^k\)是二项式系数:\(C_n^k = {\frac{n!}{k!(n-k)!}}\)
二项分布来源于牛顿二项式
\[ (a+b)^n = \sum_{k=0}^nC_n^ka^kb^{n-k} \]
8.3 二项分布与伯努利分布
- 二项分布的期望是伯努利分布期望的\(n\)倍
\[ E(x) = np \] - 二项分布的方差是伯努利分布方差的\(n\)倍
\[ D(x) = np(1-p) \]
九、贝塔分布(Beta Distribution)
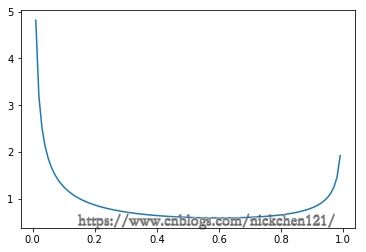
9.1 贝塔分布的概率密度函数图像
from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
a = 0.4
b = 0.6
x = np.arange(0.01, 1, 0.01)
y = stats.beta.pdf(x, a, b)
plt.plot(x, y, label='a=0.4,b=0.6')
plt.show()十、几何分布(负二项分布)(Geometric Distribution)
10.1 几何分布概率质量函数图像
十一、狄利克雷分布(多项分布的共轭分布)(Dirichlet distribution)
十二、超几何分布(Hypergeometric Distribution)
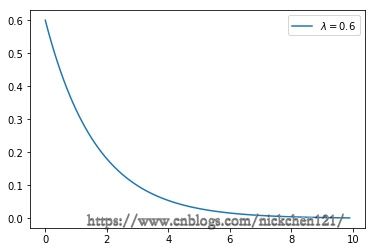
十三、指数分布(Exponential Distribution)
13.1 指数分布概率密度函数图像
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
lambd = 0.6
x = np.arange(0, 10, 0.1)
y = lambd * np.exp(-lambd*x)
plt.plot(x, y, label='$\lambda=0.6$')
plt.legend()
plt.show()