汉诺塔是有算法的。
很多问题都有解决办法,汉诺塔也不例外。如果汉诺塔的算法符合 Introduction to algorithms 这本书的观点:在计算机出现以前就有了算法,只不过计算机的出现带来了更多的算法,那么汉诺塔[1]的算法肯定不是在计算机出现之后才被发现的,只不过通过代码,一部分人可以把这个算法描述的更清晰,另外一部分人可以把这个算法看的更清晰。
另外,本文适合初学者(我就是初学者)。
C 实现
我们先用 C 语言来实现这个算法。但在写代码之前,我们要想清楚这个问题到底怎么解决,这个算法到底是什么。写代码只是写出来而已,思考问题的解决才是更重要的。
如果用语言描述解决汉诺塔问题的步骤,比较自然的会想到:
- 想办法把最大号圆盘挪到目标柱子上
- 想办法把次大号圆盘挪到目标柱子上
- ……
而把最大号圆盘挪到目标柱子上之后,次大号圆盘也就成了最大号圆盘,依此类推,后面的圆盘也是一样。所以问题永远是把当前未在目标柱子上的最大圆盘挪到目标柱子上。
另外,为了实现将最大圆盘挪到目标柱子上,必须把最大的圆盘和目标柱子暴露出来。所以总是会出现这样的局面——目标柱子上是空,或者只有安排好的几个大号圆盘(不用再考虑的圆盘),而当前未在目标柱子上的最大圆盘单独暴露出来:
这里有两个地方值得注意。
首先,在上图所示的情况中,把最大圆盘上面的各个圆盘挪到中间柱子上的问题,就是一个小规模的汉诺塔问题(问题规模小了 1 级,也就是说,汉诺塔的层数少了 1,下同)。
其次,一旦把当前未在目标柱子上的最大圆盘挪过来,问题就成了中间柱子上的汉诺塔挪到目标柱子上的问题,又是一个小规模的汉诺塔问题。
解决的这两个小规模的汉诺塔问题,就可以解决这个大一级的汉诺塔问题,但可以想象。解决小规模汉诺塔问题的时候,需要解决更小规模的汉诺塔问题。到这里,递归的身影就已经很明显了。
直到问题变成只有一个圆盘不在目标柱子上时,直接将圆盘挪过来就好了。
下面我们用 C 代码来实现这个递归,关键就是形成如上描述的两个规模小一级的汉诺塔问题。
void hanoi (int disks, char start, char mid, char dest) {
// 用 start, mid, 和 dest 分别代表起始柱子,中间柱子,和目标柱子
int b1 = disks; // 设当前最大的圆盘为 b1,这个圆盘的编号等于当前未妥善安置的圆盘的个数
int sdisks = disks - 1; // smaller disks,代表小一点的圆盘的个数
if (disks == 1) {
move(b1, start, dest);
}
else {
hanoi(sdisks, start, dest, mid); // 借助 dest 柱子,把小一点的圆盘都挪到中间柱子上,这是规模小一级的汉诺塔问题
move(b1, start, dest); // 将最大圆盘挪到目标圆盘
hanoi(sdisks, mid, start, dest); // 借助 start 柱子,把小一点的圆盘挪到目标柱子上,这是规模小一级的汉诺塔问题
}
}
这个算法中为了表述方便,建立了两个变量 b1 和 sdisks,但为了节省内存,他们可以直接用表达式代替。
void hanoi(int disks, char start, char mid, char dest) {
if (disks == 1) {
move(disks, start, dest);
}
else {
hanoi(disks - 1, start, dest, mid);
move(disks, start, dest);
hanoi(disks - 1, mid, start, dest);
}
}
另外定义 main 函数和 move 函数,就可以构成一个完整的程序了。
void move(int disk, char from, char to) {
printf("Move disk %d from %c to %c \n", disk, from, to);
}
// void hanoi here ...
int main() {
int disks;
printf("How many disks do you want? \n");
scanf("%d", disks);
hanoi(disks, 'X', 'Y', 'Z'); // 设起始,中间,目标柱子分别为 X, Y, Z
return 0;
}
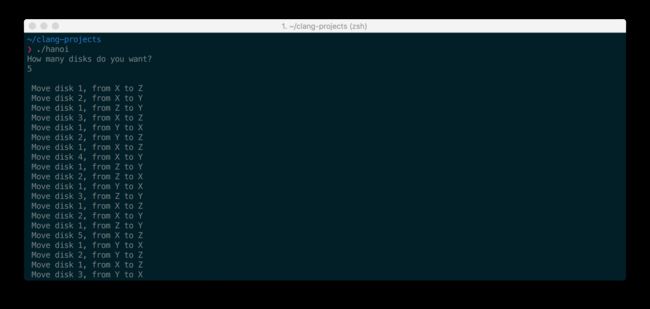
你会看到类似于下面的输出[2]:
Ruby 实现
下面我们再用 Ruby 写一遍这个算法,核心都是一样的:为了递归解决问题,让 #hanoi 函数调用自己。
def hanoi(disks, start, mid, dest)
if disks == 1
move(1, start, dest)
return
end
hanoi(disks - 1, start, dest, mid)
move(disks, start, dest)
hanoi(disks - 1, mid, start, dest)
end
def move(disk, from, to)
puts("Move disk #{disk} from #{from} to #{to}")
end
puts "How many towers do you want?"
disks = gets.chomp.to_i
hanoi(disks, 'X', 'Y', 'Z')
数据结构
如果汉诺塔的层数特别多,也就是你给 disks 赋一个特别大的值,你觉得会怎么样?
c 中会说 segmentation fault,这是和内存分配有关的错误。 ruby 中会说 stack level too deep (SystemStackError)—— 栈太深了, 报错位置就是 #hanoi 中第一个调用自己的地方 hanoi(disks - 1, start, dest, mid)。
会出现这个错误的原因在于函数的调用在数据结构上是把一个新函数加载到函数的调用栈中。最先调用的函数(在本例中是主函数中的 hanoi 函数)在栈底,如果这个函数又去调用了别的函数,则这个函数停在调用位置,新函数被压入栈中。如果新函数又调用了另外一个新函数,则继续压入栈中,以此类推。这就是调用函数进栈的过程。
直到有某个刚刚压入栈中的函数(也就是处在栈顶位置的函数)不再调用别的函数,而是有了返回结果,则此函数退栈,栈顶位置转移到此函数调用者所在的位置;此调用者继续退栈,向更之前的函数返回结果,然后自己退栈。又以此类推,这就是函数返回结果的过程,是一个退栈的过程。
那么,返回的结果怎么交给调用他的函数呢?也就是栈的下一层。方法是在新的函数被调用的时候,被压入栈中的,除了参数,还有调用函数的返回地址。这样,他被调用函数有了返回结果,就可以按照之前保存的返回地址找到调用函数,向其传递返回结果。
汉诺塔中的递归,能让我们感受到这种调用,尽管每次调用的所谓的新函数,都是他自己。
-
这个游戏在1883年就被发明了 ↩
-
当然,C 需要编译一下,
make hanoi如果你的文件名是 hanoi.c 的话 ↩