使用WebGL绘制地球

首先陈述——本篇内容基于《WebGL编程指南》书籍以及http://www.hiwebgl.com/?p=339

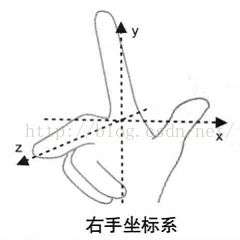
现在，在正式绘制地球前，我们先来了解下左右手坐标系

定义：在空间直角坐标系中，让右手拇指指向X轴的正方向，食指指向Y轴正方向，如果中值能指向Z轴正方向，则称这个坐标系为右手直角坐标系。反之称为左手直角坐标系（左手中指指向Z轴正方向）。

那么在WebGL/OpenGL中使用的是左手还是右手坐标系呢？

在发布的OpenGL ES 2.0（也是WebGL的基础）的官方手册中，说明了“GL图形语言不强制使用左手坐标系或右手坐标系”

        也就是说，WebGL对使用左手或右手坐标系这个问题上是中立的，那为什么诸多书籍和教程，都讲WebGL的坐标系统描述为右手的呢？

这是因为使用右手坐标系是个传统。当开发自己的程序时，你需要确定自己使用的坐标系统，然后不再改变。这一点对你自己的程序成立，对那些已经开发出来的、帮助开发者使用WebGL（和OpenGL）的各种图形库也成立。早起图形库中的大部分都采用了右手坐标系。时至今日，右手坐标系统已经成为了传统，以致似乎成了GL图形语言的一部分，这就导致人们都认为GL图形语言就是右手坐标系的。

其实，WebGL的 默认行为，比如，在裁剪空间中使用左手坐标系与右手坐标系冲突，为了解决这个冲突，我们可以通过翻转Z坐标值进行补偿，这样就能够继续使用传统的右手坐标系了。但是，使用右手坐标系只是一个传统，只是大多数人遵守而已。

现在，我们可以明确指出，本次我们绘制的地球，使用的是右手坐标系！

接下来，我们来了解一下经纬度，如果不按经纬度绘制地球，而采用WebGL默认的方式绘制地球，不符合我们正常思维逻辑！

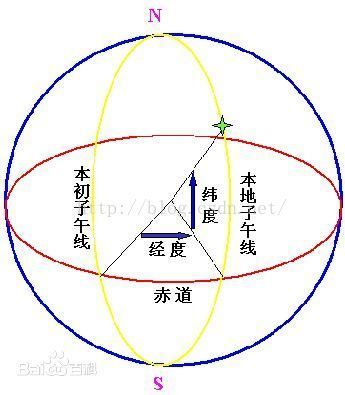
这张图非常清晰的指明了经纬度是如何指定的，绿色星星代表地面上的某个位置。

纬度（latitude）的计算是：连接地心与该点，形成的直线与赤道平面的夹角即为纬度。

经度（longitude）的计算是：该点投影到赤道平面上形成的点，这个点与地心连接成的线与本初子午线投影到赤道平面的直线形成的角即是经度。

赤道以北的纬度，叫北纬，习惯上用“N”作代号；赤道以南的纬度，叫南纬，习惯上用“S”作代号。北纬、南纬各有90度。北极和南极分别是90度N和90度S。

        经度是地球上一个地点离一根被称为本初子午线的南北方向走线以东或以西的度数。本初子午线的经度是0°，地球上其它地点的经度是向东到180°或向西到180°。

在此，纬度范围是-90°~90°（其实应该是南极到赤道：90°~0°，然后从赤道到北极：0°~90°，但为了在坐标轴上描述实际情况，我们表示-90°~90°），经度范围是-180°~180°（同理）

 

于是，我们便可绘制地球了，根据人们思维习惯，我们将WebGL使用的右手坐标系进行翻转：

右边的坐标系是左边坐标系经过翻转后得到的，其实两个坐标系都是一个坐标系（右手坐标系），只是从不同的角度来看待而已。因为翻转后的坐标系满足大地坐标系（地理坐标系）的定义，此时便可通过经纬度坐标来描述不同位置。

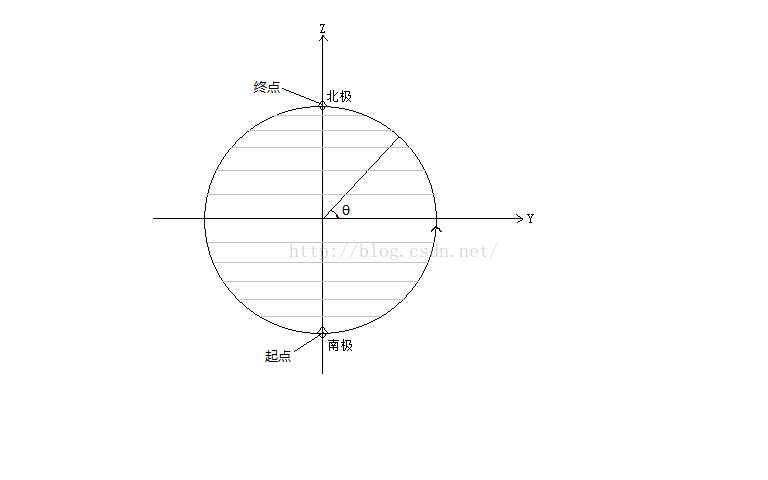
首先我们定义纬度方向是从南极到北极，也即是从-90°~90°，我们定义连接线与XY平面的夹角为θ，我们可以根据θ的值来计算出每条纬线。每个半圆的弧度是π，所以θ的取值应该是从-π/2一直到π/2。这样我们就可以确保我们用纬线平均的将球体分割开来。假设定义有50个纬度带，那么我们可以将θ角表示为nπ/50 - π/2，n表示从0到50。于是便可表示从南极到北极。

在每个确定的纬线上的点，不管他们的经度如何，都有相同的Z坐标。我们可以推出，在这个用50条纬线平均分割且半径为1的球体上，第n条纬线的Z坐标是sin(nπ/50 - π/2)，范围是从-1到1。

 

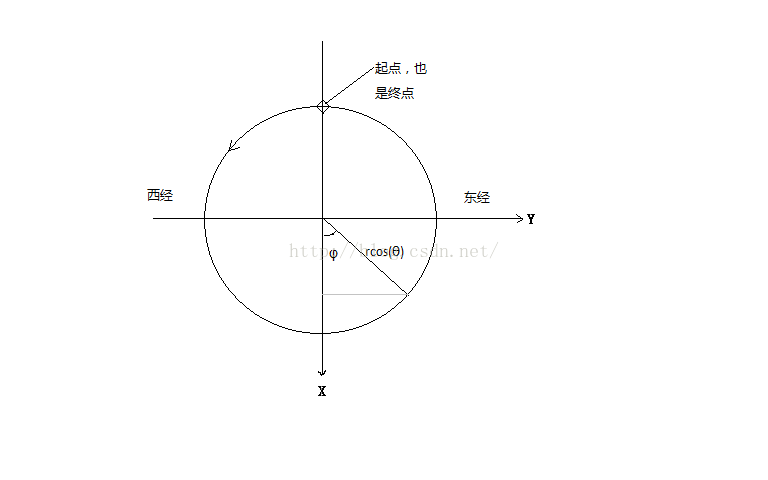
接下来定义经度方向是从西经到东经，也即是从-180°~180°，来计算X,Y坐标，我们在第n条纬线上，水平将球体切开，可以看到圆的半径是cos(nπ/50 - π/2)，假设为k。如果我们用经线将这个圆平均分割一下，假设是50条经线，将本初子午线投影到这个水平面上，形成一条直线，假设这条直线和经线与圆的交点之间的夹角为φ，又有整个圆的弧度为2π，那么φ的取值应该是0到2π，因为需要从-180°~180°，所以φ的取值应该为n2π/50 – π，n表示从0到50。于是便可表示从西经到东经。

此时将经线与圆的交点投影到X和Y坐标上，已知φ，便可得到X为kcos(φ)，Y为ksin(φ)。

 

由此，可知x,y,z的值为：

x = rcos(θ) cos(φ)

y = rcos(θ) sin(φ)

z = rsin(θ)

 

以上就是我们如何计算出顶点的过程。接下来是计算纹理坐标，我们希望纹理贴图的提供者，提供给我们的是一张矩形图片。多说一句，WebGL（不是Javascript）会被其他形状的贴图搞晕。这样，我们就可以放心的假定，这张纹理图片的顶部和底部拉伸肯定是遵循墨卡托投影法则（Mercator Projection）的。这样就是说，我们可以从左到右按照经线平均分割纹理图片得出坐标u，从上到下按照纬线平均分割纹理图片得到坐标v。

好了，这就是全部的工作原理。对于Javascript来说，理解并运算以上原理是如此难以置信得简单方便！我们只需要循环遍历所有的纬线切片，在循环内我们再遍历所有的经线切片，之后我们就可以计算出纹理坐标和顶点位置。唯一需要注意的是，在循环结束的条件中，循环变量必须大于经线或纬线的数量。所以这里我们必须使用小于等于而不是小于。也就是说，比如有50条经线，在每条纬线上就会产生51个顶点。因为根据三角函数的循环，最后一个顶点和第一个顶点的位置其实是相同的，这样的一个重叠让我们把所有东西都连接到了一起。

var latitudeBands = 50;//纬度带
var longitudeBands = 50;//经度带
var positions = [];//存储x，y，z坐标
var indices = [];//三角形列表（索引值）
var textureCoordData = [];//存储纹理坐标u，v，纹理坐标与顶点坐标一一对应

for(var latNum = 0; latNum <= latitudeBands; latNum++){
    var lat = latNum * Math.PI / latitudeBands - Math.PI / 2;//纬度范围从-π/2到π/2
    var sinLat = Math.sin(lat);
    var cosLat = Math.cos(lat);

    for(var longNum = 0; longNum <= longitudeBands; longNum++){
        var lon = longNum * 2 * Math.PI / longitudeBands - Math.PI;//经度范围从-π到π
        var sinLon = Math.sin(lon);
        var cosLon = Math.cos(lon);

        var x = cosLat * cosLon;
        var y = cosLat * sinLon;
        var z = sinLat;
        var u = (longNum / longitudeBands);
        var v = (latNum / latitudeBands);

        positions.push(x);
        positions.push(y);
        positions.push(z);
        textureCoordData.push(u);
        textureCoordData.push(v);
    }
}

现在我们已经处理完顶点了，还需要把它们缝合到一起。我们生成一个顶点索引列表，将每个四边形分成一对三角形。

for(var latNum = 0; latNum < latitudeBands; latNum++){
    for(var longNum = 0; longNum < longitudeBands; longNum++){
        var first = latNum * (longitudeBands + 1) + longNum;
        var second = first + longitudeBands + 1;

        indices.push(first);
        indices.push(first + 1);
        indices.push(second);

        indices.push(second);
        indices.push(second + 1);
        indices.push(first + 1);
    }
}

var vertices = new Float32Array(positions);
var indices = new Uint16Array(indices);
var texCoord = new Float32Array(textureCoordData);

	我们通过循环遍历了所有顶点，对于每个顶点，我们将其索引值储存在first变量中，然后向前数longitudeBands + 1个顶点，找到和它配对的下一个纬线带，储存在second变量中（之所以+1是因为我们额外增加的那一个顶点会重叠）。这样我们就生成了两个三角形，如图所示。

好了，以上就是我们的绘制地球的核心代码，包含了顶点坐标和纹理坐标，接下来就可以贴纹理，设置观察点坐标……，这些便不再陈述。

 

现在，让我们验证一下，

观察北极，视点坐标为0,0,5，观察目标点坐标为0,0,0，上方向坐标为0,1,0

观察南极，视点坐标为0,0,-5，观察目标点坐标为0,0,0，上方向坐标为0,1,0

观察本初子午线，视点坐标为5,0,0，观察目标点坐标为0,0,0，上方向坐标为0,0,1

通过以上的描述，我们便可直接操作经纬度来映射到我们的坐标系统中，这符合我们的思维，既然建立了可描述的地球模型，接下来便可对该模型进行各种操作……