TensorFlow：Chap6笔记总结（卷积神经网络CNN）

1.卷积神经网络简介

       先给图。

图1 全连接神经网络与卷积神经网络结构示意图

       在全连接神经网络中，每相邻两层之间的节点都有边相连，于是一般会将每一层全连接层中的节点组织成一列，这样方便显示连接结构。而对于卷积神经网络，相邻两层之间只有部分节点相连，为了展示每一层神经元的维度，一般会将每一层卷积层的节点组织成一个三维矩阵。

        卷积神经网络和全连接神经网络的唯一区别在于神经网络中相邻两层的连接方式。

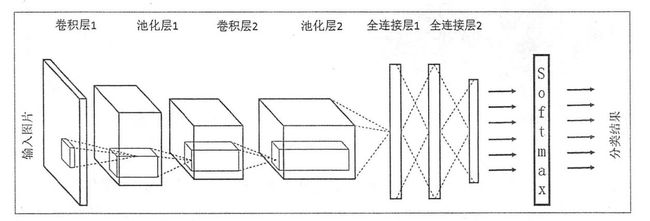
图2 用于图像分类问题的一种卷积神经网络架构图

        一个卷积神经网络主要由以下五种结构组成：

      （1）输入层

             输入层是整个神经网络的输入，在处理图像的卷积神经网络中，它一般代表了一张图片的像素矩阵。从输入层开始，卷积神经网络通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵，直到最后的全连接层。

      （2）卷积层

            卷积层中每一个节点的输入只是上一层神经网络的一小块，这个小块常用的大小有3×3或5×5。卷积层试图将神经网络中的每一小块进行更加深入地分析从而得到抽象程度更高的特征。一般通过卷积层处理过的节点矩阵会变得更深。

      （3）池化层

           池化层神经网络不会改变三维矩阵的深度，但可以缩小矩阵的大小。池化操作可以认为是将一张分辨率较高的图片转化为分辨率较低的图片。通过池化层，能进一步缩小最后全连接层中的节点数，达到减少整个神经网络中参数的目的。

      （4）全连接层

           可以将卷积层和池化层看成自动图像特征提取的过程。在特征提取完成后，需要使用全连接层来完成分类任务。

      （5）Softmax层

          用于分类问题，得到当前样例属于不同种类的概率分布情况。

2.卷积神经网络常用结构

2.1 卷积层

        过滤器（filter）。过滤器能将当前层神经网络上的一个子节点矩阵转化为下一层神经网络上的一个单位节点矩阵。单位节点矩阵是指一个长和宽都为1，但深度不限的节点矩阵。          

  

图3 卷积层过滤器结构图

       常用的过滤器尺寸有3×3或5×5。过滤器尺寸指的是一个过滤器输入节点矩阵的大小，而深度是指输出单位节点矩阵的深度。

       过滤器在此不作过多描述，欢迎提问。

       卷积层结构的前向传播过程就是通过将一个过滤器从神经网络当前层的左上角移动到右下角，并且在移动中计算每一个对应的单位矩阵得到的。图4给出卷积层前向传播的计算流程。

图4 卷积层前向传播过程

        点乘之后，上图计算最右下角的0应该为-2，书上计算有误？

2.2 池化层

         池化层可以有效缩小矩阵尺寸，从而减少最后全连接层中的参数。使用池化层既可以加快计算速度也能防止过拟合问题。使用最大值操作的池化层称为最大池化层（max pooling），使用平均值操作的池化层称为平均池化层（average pooling）。

          卷积层和池化层中过滤器移动方式相似，区别在于卷积层使用的过滤器是横跨整个深度，而池化层使用的过滤器只影响一个深度上的节点，所以池化层的过滤器除了在长和宽两个维度移动外，还需在深度维度移动。

 

图5 一个最大池化层前向传播计算过程（使用了全0填充且步长为2）

3.经典卷积网络——LeNet-5模型

3.1 LeNet-5模型

        LeNet-5模型是Yann LeCun教授在1998年《Gradient-based learning applied to document recognition》中提出。它是第一个成功应用于数字识别问题的卷积神经网络。在MNIST数据集上，可以达到99.2%的正确率。模型结构共有7层，如图6所示。

图6 LeNet-5模型结构图

       第一层：卷积层

            输入层大小为32×32×1。过滤器尺寸为5×5，深度为6，不使用全0填充，步长为1。输出尺寸为32-5+1=28，深度为6。该层共有5×5×1×6+6=156个参数，其中6个为偏置项参数。下一层节点矩阵有28×28×6=4704个节点，每个节点和5×5=25个当前层节点相连，所以本层共有4704×（25+1）=122304个连接。

       第二层：池化层

           该层输入为第一层输出，大小为28×28×6的节点矩阵。本层采用过滤器大小为2×2，长宽步长均为2，所以本层输出矩阵大小为14×14×6。

       第三层：卷积层

           本层的输入矩阵大小为14×14×6，过滤器尺寸为5×5，深度为16。本层不使用全0填充，步长为1。输出矩阵大小为10×10×16。本层有5×5×6×16+16=2416个参数，共有10×10×16×（25+1）=41600个连接。

       第四层：池化层

           本层输入矩阵大小为10×10×16，采用过滤器大小为2×2，步长为2，本层输出矩阵大小为5×5×16。

       第五层：全连接层

           本层输入矩阵大小为5×5×16，在LeNet-5模型论文中将该层称为卷积层，但因为过滤器大小为5×5，所以和全连接层没区别，实现过程中将本层堪称全连接层。本层输出节点个数为120，共有5×5×16×120+120=48120个参数。

       第六层：全连接层

           本层输入节点个数为120，输出节点个数为84个，总共参数为120×84+84=10164个。

       第七层：全连接层

              本层输入节点个数为84，输出节点个数为10个，总共参数为84×10+10=850个。

3.2 类LeNet-5模型的卷积神经网络TensorFlow实现

（1）MNIST最佳实践样例程序

mnist_inference.py

import tensorflow as tf

# 1. 定义神经网络结构相关的参数
INPUT_NODE = 784
OUTPUT_NODE = 10
LAYER1_NODE = 500

# 2. 通过tf.get_variable函数来获取变量
def get_weight_variable(shape, regularizer):
    weights = tf.get_variable("weights", shape, initializer=tf.truncated_normal_initializer(stddev=0.1))
    if regularizer != None:
        tf.add_to_collection('losses', regularizer(weights))
    return weights

# 3. 定义神经网络的前向传播过程
def inference(input_tensor, regularizer):
    with tf.variable_scope('layer1'):
        weights = get_weight_variable([INPUT_NODE, LAYER1_NODE], regularizer)
        biases = tf.get_variable("biases", [LAYER1_NODE], initializer=tf.constant_initializer(0.0))
        layer1 = tf.nn.relu(tf.matmul(input_tensor, weights) + biases)

    with tf.variable_scope('layer2'):
        weights = get_weight_variable([LAYER1_NODE, OUTPUT_NODE], regularizer)
        biases = tf.get_variable("biases", [OUTPUT_NODE], initializer=tf.constant_initializer(0.0))
        layer2 = tf.matmul(layer1, weights) + biases

    return layer2

mnist_train.py

import os
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import mnist_inference

#配置神经网络的参数
BACTH_SIZE = 100
LEARNING_RATE_BASE = 0.8
LEARNING_RATE_DECAY = 0.99
REGULARAZTION_RATE = 0.0001
TRAINING_STEPS = 5000
MOVING_AVERAGE_DECAY = 0.99
#模型保存的路径和文件名
MODEL_SAVE_PATH = "/path/to/model/"
MODEL_NAME = "model.ckpt"

def train(mnist):
	# 定义输入输出的placeholder
	x = tf.placeholder(tf.float32, [None, mnist_inference.INPUT_NODE],name='x-input')
	y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE],name='y-input')
	regularizer = tf.contrib.layers.l2_regularizer(REGULARAZTION_RATE)
	# 直接使用mnist_inference.py定义的前向传播结果
	y = mnist_inference.inference(x, regularizer)
	global_step = tf.Variable(0, trainable=False)

	#定义损失函数、学习率、滑动平均操作及训练过程
	variable_average = tf.train.ExponentialMovingAverage(
		MOVING_AVERAGE_DECAY, global_step)
	variable_average_op = variable_average.apply(
		tf.trainable_variables())
	cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_,1))
	#cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(y,tf.argmax(y_,1))
	cross_entropy_mean = tf.reduce_mean(cross_entropy)
	loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
	learning_rate = tf.train.exponential_decay(
		LEARNING_RATE_BASE,
		global_step,
		mnist.train.num_examples / BACTH_SIZE,LEARNING_RATE_DECAY,
		staircase = True)
	train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=global_step)
	with tf.control_dependencies([train_step,variable_average_op]):
		train_op = tf.no_op(name='train')

	# 初始化TensorFlow持久化类
	saver = tf.train.Saver()
	with tf.Session() as sess:
		tf.initialize_all_variables().run()

		# 在训练过程中不再测试模型在验证数据上的表现，验证和测试的过程将会有一个独立的程序来完成
		for i in range(TRAINING_STEPS):
			xs,ys = mnist.train.next_batch(BACTH_SIZE)
			_,loss_value,step = sess.run([train_op,loss,global_step],
										 feed_dict={x:xs,y_:ys})
			# 每1000轮保存一次模型
			if i % 1000 == 0:
				# 输出当前的训练情况
				print("After %d training step(s),loss on training batch is %g." % (step, loss_value))
				# 保存当前模型
				saver.save(
					sess,os.path.join(MODEL_SAVE_PATH,MODEL_NAME),global_step=global_step)
def main(argv=None):
	mnist = input_data.read_data_sets("/tmp/data",one_hot=True)
	train(mnist)

if __name__ == '__main__':
	main()

mnist_eval.py

import time
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

# 加载mnist_inference.py和mnist_train.py中定义的常量和函数
import mnist_inference
import mnist_train

# 每隔10秒加载一次最新的模型，并在测试数据上测试最新模型的正确率
EVAL_INTERVAL_SECS = 10

def evaluate(mnist):
	with tf.Graph().as_default() as g:
		# 定义输入输出格式
		x = tf.placeholder(tf.float32, [None, mnist_inference.INPUT_NODE], name='x-input')
		y_ = tf.placeholder(tf.float32, [None,mnist_inference.OUTPUT_NODE],name='y-input')
		validate_feed = {x:mnist.validation.images,
						 y_:mnist.validation.labels}

		# 直接调用封装好的函数来计算前向传播的结果。
		y = mnist_inference.inference(x, None)

		# 使用前向传播的结果计算正确率。使用tf.argmax(y,1)得到输入样例的预测类别
		correct_prediction = tf.equal(tf.argmax(y, 1),tf.argmax(y_, 1))
		accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

		# 通过变量重命名的方式来加载模型，这样在前向传播的过程中就不需要调用求滑动 #
		# 平均的函数来获取平均值了。这样就可以完全公用mnist_inference.py中定义的 #
		# 前向传播过程 #
		variable_averages = tf.train.ExponentialMovingAverage(
			mnist_train.MOVING_AVERAGE_DECAY)
		variable_to_restore = variable_averages.variables_to_restore()
		saver = tf.train.Saver(variable_to_restore)

		# 每隔EVAL_INTERVAL_SECS秒调用一次计算正确率的过程以检测训练过程中正确率的变化
		while True:
			with tf.Session() as sess:
				# tf.train.get_checkpoint_state函数会通过checkpoint文件自动找到目录中最新模型的文件名
				ckpt = tf.train.get_checkpoint_state(
					mnist_train.MODEL_SAVE_PATH)
				if ckpt and ckpt.model_checkpoint_path:
					# 加载模型
					saver.restore(sess, ckpt.model_checkpoint_path)
					# 通过文件名得到模型保存时迭代的轮数
					global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]
					accuracy_score = sess.run(accuracy, feed_dict=validate_feed)
					print("After %s training step(s), validation accuracy = %g" % (global_step, accuracy_score))
				else:
					print('No checkpoint file found')
					return
				time.sleep(EVAL_INTERVAL_SECS)
def main(argv=None):
	mnist = input_data.read_data_sets("/tmp/data",one_hot=True)
	evaluate(mnist)

if __name__ == '__main__':
	main()

（2）用TensorFlow实现一个类似LeNet-5模型的卷积神经网络来解决MNIST数字识别问题。

LeNet5_inference.py。

import tensorflow as tf

# 1.配置参数
INPUT_NODE = 784
OUTPUT_NODE = 10

IMAGE_SIZE = 28
NUM_CHANNELS = 1
NUM_LABELS = 10
# 第一层卷积层的尺寸和深度
CONV1_DEEP = 32
CONV1_SIZE = 5
# 第二层卷积层的尺寸和深度
CONV2_DEEP = 64
CONV2_SIZE = 5
# 全连接层的节点个数
FC_SIZE = 512

# 2.定义前向传播的过程
# 这里添加了一个新的参数train，用于区分训练过程和测试过程。
# 在这个程序中将用到dropout方法，dropout可以进一步提升模型可靠性并防止过拟合
# dropout过程只在训练时使用
def inference(input_tensor, train, regularizer):
	# 声明第一层卷积层的变量并实现前向传播过程。
	# 通过使用不同的命名空间来隔离不同层的变量
	# 这可以让每一层中的变量命名只需要考虑在当前层的作用。不需要担心重名的问题
	# 定义的卷积层输入为28*28*1的原始MNIST图片像素，使用全0填充后，输出为28*28*32
	with tf.variable_scope('layer1-conv1'):
		conv1_weights = tf.get_variable(
			"weight",[CONV1_SIZE,CONV1_SIZE,NUM_CHANNELS,CONV1_DEEP],
			initializer=tf.truncated_normal_initializer(stddev=0.1))
		conv1_biases = tf.get_variable("bias",[CONV1_DEEP],initializer=tf.constant_initializer(0.0))
		conv1 = tf.nn.conv2d(input_tensor, conv1_weights, strides=[1,1,1,1],padding='SAME')
		relu1 = tf.nn.relu(tf.nn.bias_add(conv1,conv1_biases))

	# 实现第二层池化层的前向传播过程。这一层输入为14*14*32
	with tf.name_scope('layer2-pool1'):
		pool1 = tf.nn.max_pool(relu1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

	# 实现第三层卷积层
	with tf.variable_scope('layer3-conv2'):
		conv2_weights = tf.get_variable(
			"weight",[CONV2_SIZE, CONV2_SIZE, CONV1_DEEP, CONV2_DEEP],
			initializer=tf.truncated_normal_initializer(stddev=0.1)
		)
		conv2_biases = tf.get_variable("bias",[CONV2_DEEP],initializer=tf.constant_initializer(0.0))

		conv2 = tf.nn.conv2d(pool1, conv2_weights, strides=[1,1,1,1], padding='SAME')
		relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))

	# 实现第四层池化层
	with tf.name_scope('layer4-pool2'):
		pool2 = tf.nn.max_pool(relu2, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')
		# 将第四层池化层的输出转化为第五层全连接的输入格式。
		pool_shape = pool2.get_shape().as_list()
		# 计算将矩阵拉直成向量之后的长度，这个长度就是矩阵长度及深度的乘积。
		nodes = pool_shape[1]* pool_shape[2]*pool_shape[3]
		# 通过tf.reshape函数将第四层的输出变成一个batch的向量
		reshaped = tf.reshape(pool2, [pool_shape[0],nodes])

	#声明第五层全连接层的变量并实现前向传播过程
	with tf.variable_scope('layer5-fc1'):
		fc1_weights = tf.get_variable(
			"weight", [nodes, FC_SIZE],
			initializer=tf.truncated_normal_initializer(stddev=0.1)
		)
		if regularizer != None:
			tf.add_to_collection('losses', regularizer(fc1_weights))
		fc1_biases = tf.get_variable("bias", [FC_SIZE], initializer=tf.constant_initializer(0.1))
		fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights)+fc1_biases)
		if train:fc1 = tf.nn.dropout(fc1,0.5)

	# 声明第六层全连接层的变量并实现前向传播过程
	with tf.variable_scope('layer6-fc2'):
		fc2_weights = tf.get_variable(
			"weight", [FC_SIZE,NUM_CHANNELS], initializer=tf.truncated_normal_initializer(stddev=0.1)
		)
		if regularizer != None:
			tf.add_to_collection('losses',regularizer(fc2_weights))
		fc2_biases = tf.get_variable(
			"bias",[NUM_LABELS],initializer=tf.constant_initializer(0.1)
		)
		logit = tf.matmul(fc1, fc2_weights)+ fc2_biases
		return logit

LeNet5_train.py训练模型

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import LeNet5_infernece
import os
import numpy as np

# 1.定义神经网络相关参数
BACTH_SIZE = 100
LEARNING_RATE_BASE = 0.01
LEARNING_RATE_DECAY = 0.99
REGULARAZTION_RATE = 0.0001
TRAINING_STEPS = 5000
MOVING_AVERAGE_DECAY = 0.99
#模型保存的路径和文件名
MODEL_SAVE_PATH = "LeNet5_model/"
MODEL_NAME = "LeNet5_model"

# 2.定义训练过程
def train(mnist):
	# 定义输入输出的placeholder
	x = tf.placeholder(tf.float32,[
		BACTH_SIZE,
		LeNet5_infernece.IMAGE_SIZE,
		LeNet5_infernece.IMAGE_SIZE,
		LeNet5_infernece.NUM_CHANNELS],
					name='x-input')
	y_ = tf.placeholder(tf.float32, [None, LeNet5_infernece.OUTPUT_NODE],name='y-input')
	regularizer = tf.contrib.layers.l2_regularizer(REGULARAZTION_RATE)
	y = LeNet5_infernece.inference(x, True, regularizer)
	global_step = tf.Variable(0, trainable=False)

	# 定义损失函数、学习率、滑动平均操作及训练过程
	variable_average = tf.train.ExponentialMovingAverage(
		MOVING_AVERAGE_DECAY, global_step)
	variable_average_op = variable_average.apply(
		tf.trainable_variables())
	cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
	cross_entropy_mean = tf.reduce_mean(cross_entropy)
	loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
	learning_rate = tf.train.exponential_decay(
		LEARNING_RATE_BASE,
		global_step,
		mnist.train.num_examples / BACTH_SIZE, LEARNING_RATE_DECAY,
		staircase=True)
	train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
	with tf.control_dependencies([train_step, variable_average_op]):
		train_op = tf.no_op(name='train')

	# 初始化TensorFlow持久化类
	saver = tf.train.Saver()
	with tf.Session() as sess:
		tf.global_variables_initializer().run()

		# 在训练过程中不再测试模型在验证数据上的表现，验证和测试的过程将会有一个独立的程序来完成
		for i in range(TRAINING_STEPS):
			xs,ys = mnist.train.next_batch(BACTH_SIZE)
			reshaped_xs = np.reshape(xs,(
				BACTH_SIZE,
				LeNet5_infernece.IMAGE_SIZE,
				LeNet5_infernece.IMAGE_SIZE,
				LeNet5_infernece.NUM_CHANNELS))
			_, loss_value, step = sess.run([train_op, loss, global_step],
										   feed_dict={x: reshaped_xs, y_: ys})
			# 每1000轮保存一次模型
			if i % 1000 == 0:
				# 输出当前的训练情况
				print("After %d training step(s),loss on training batch is %g." % (step, loss_value))
				# 保存当前模型
				saver.save(
					sess,os.path.join(MODEL_SAVE_PATH,MODEL_NAME),global_step=global_step)
def main(argv=None):
	mnist = input_data.read_data_sets("/tmp/data",one_hot=True)
	train(mnist)

if __name__ == '__main__':
	main()

LeNet5_eval.py测试模型

import tensorflow as tf
import time
import math
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

import LeNet5_infernece
import LeNet5_train

def evaluate(mnist):
	with tf.Graph().as_default() as g:
		x = tf.placeholder(tf.float32, [
			mnist.test.num_examples,
			LeNet5_infernece.IMAGE_SIZE,
			LeNet5_infernece.IMAGE_SIZE,
			LeNet5_infernece.NUM_CHANNELS],
						   name='x-input')
		y_ = tf.placeholder(tf.float32, [None,LeNet5_infernece.OUTPUT_NODE],name='y-input')
		validate_feed = {x:mnist.test.images,
						 y_:mnist.test.labels}
		global_step =tf.Variable(0,trainable=False)
		regularizer = tf.contrib.layers.l2_regularizer(LeNet5_train.REGULARAZTION_RATE)

		# 直接调用封装好的函数来计算前向传播的结果。
		y = LeNet5_infernece.inference(x, False, regularizer)

		# 使用前向传播的结果计算正确率。使用tf.argmax(y,1)得到输入样例的预测类别
		correct_prediction = tf.equal(tf.argmax(y, 1),tf.argmax(y_, 1))
		accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

		# 通过变量重命名的方式来加载模型，这样在前向传播的过程中就不需要调用求滑动 #
		# 平均的函数来获取平均值了。这样就可以完全公用mnist_inference.py中定义的 #
		# 前向传播过程 #
		variable_averages = tf.train.ExponentialMovingAverage(
			LeNet5_train.MOVING_AVERAGE_DECAY)
		variable_to_restore = variable_averages.variables_to_restore()
		saver = tf.train.Saver(variable_to_restore)

		# 每隔EVAL_INTERVAL_SECS秒调用一次计算正确率的过程以检测训练过程中正确率的变化
		n = math.ceil(mnist.test.num_examples / mnist.test.num_examples)
		for i in range(n):
			with tf.Session() as sess:
				ckpt = tf.train.get_checkpoint_state(LeNet5_train.MODEL_SAVE_PATH)
				if ckpt and ckpt.model_checkpoint_path:
					saver.restore(sess, ckpt.model_checkpoint_path)
					global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]
					xs, ys = mnist.test.next_batch(mnist.test.num_examples)
					# xs, ys = mnist.test.next_batch(LeNet5_train.BATCH_SIZE)
					reshaped_xs = np.reshape(xs, (
						mnist.test.num_examples,
						# LeNet5_train.BATCH_SIZE,
						LeNet5_infernece.IMAGE_SIZE,
						LeNet5_infernece.IMAGE_SIZE,
						LeNet5_infernece.NUM_CHANNELS))
					accuracy_score = sess.run(accuracy, feed_dict={x: reshaped_xs, y_: ys})
					print("After %s training step(s), test accuracy = %g" % (global_step, accuracy_score))
				else:
					print('No checkpoint file found')
					return


# 主程序
def main(argv=None):
	mnist = input_data.read_data_sets("/tmp/data", one_hot=True)
	evaluate(mnist)


if __name__ == '__main__':
	main()

       模型跑出来结果正确率相比上一篇还高，但用时很久。

       如何设计卷积神经网络的架构？下面给出的正则表达式总结了一些经典的用于图片分类问题的卷积神经网络架构：

                                   输入层→（卷积层+→池化层？）+→全连接层+

       “卷积层+”表示一层或多层卷积层，大部分卷积神经网络中一般最多连续使用三层卷积层。“池化层？”表示没有或一层池化层。在多轮卷积层和池化层后，卷积神经网络在输出之前一般会经过1~2个全连接层。LeNet-5模型结构表示如下：

输入层→卷积层→池化层→卷积层→池化层→全连接层→全连接层→输出层

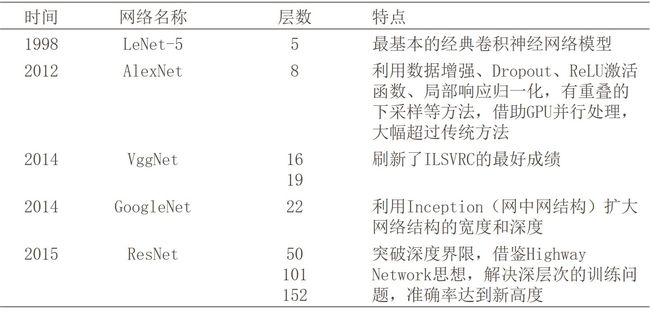
           一些经典网络特点对比如下：

        接下来熟悉其他CNN网络结构模型，同时了解RNN（循环神经网络）。