Python机器学习，聚类分析从时空聚类开始，听大佬解读时空聚类

时空聚类：

时间聚类分析，TCA算法的思想就是确定在一个序列图像上所有点是在什么时间出现变化（响应）极大值（极小值），而忽略其他细节。
1.最近邻分析
利用各个点与其最近邻点的距离，判断该点是呈随机的、规则的还是聚集的分布模式。
最近邻是一个比率值，是观测的平均距离与假定随机分布时期望平均距离的比率。
计算如下：

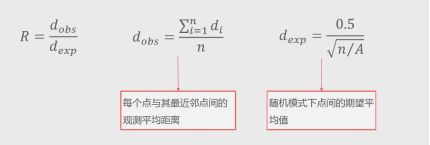
如果点的分布模式比随机模式聚集，则比率小于1；若离散，则比率大于1。
2.莫兰指数
最近邻分析只考虑点与点之间的距离，莫兰指数考虑点的位置和属性的聚集。

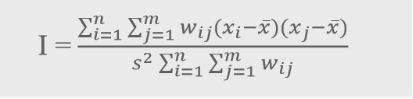
xi为点i处的值；xj为点i的邻近点j的值；
wij用于量测空间自相关的权重，一般是点i与 点j间距离的倒数，即距离衰减；
s是x值的方差。
莫兰指数取决于随机模式下的期望值：

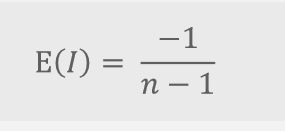
随机模式下，莫兰指数接近于E(I)；
若相邻的点并具有相近的值，则大于E(I)；
若相 邻的点为不等的值，则小于E(I)。
3.G统计量
莫兰指数只能检测出具有相近值的点是否呈现聚集状态，而不能说明集群是高值还是低值组成。

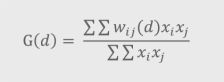
Xi为点i处的值，xj为位于点i的d距离范围之内的点j处的值xj；
wij(d)为空间权重，如莫兰指数里的 距离倒数。
G(d)的期望值为：

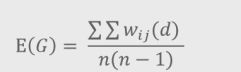
G(d) 值高，则为高值集群；
相反，则为低值集群。
但具体高至何种程度判断为高值聚集区、低至何种程度判断为低值聚集区，需要定量化Z得分值。
4.常用聚类：层次聚类、Meanshift聚类等
a.层次聚类：
层次聚类算法根据层次分解的顺序分为：自下底向上和自上向下，即凝聚的层次聚类算法和分裂的层次聚类算法（agglomerative和divisive）。
自下而上法就是一开始每个个体（object）都是一个类，然后根据linkage寻找同类，最后形成一个“类”。
自上而下法就是反过来，一开始所有个体都属于一个“类”，然后根据linkage排除异己，最后每个个体都成为一个“类”。

例：

from cluster import * 
data = [(1,12,20),(2,15,18),(3,12,16),(4,34,56),(5,28,45),(6,32,46),(7,96,13)] 
cl=HierarchicalClustering(data,lambdax,y:math.sqrt((x[1]-y[1])*(x[1]-y[1])+(x[2]-y[2])*(x[2]y[2])) )
dist_threshold = 15 
cl.getlevel(dist_threshold)

[[(7, 96, 13)], [(3, 12, 16), (1, 12, 20), (2, 15, 18)], [(4, 34, 56), (5, 28, 45), (6, 32, 46)]]

其中，lambda x,y: 
x和y指的是data数组中的两个比较数据项。x[0]是ID号，x[1]和x[2]是矢量值。 
math.sqrt((x[1]y[1])*(x[1]-y[1]) + (x[2]-y[2])*(x[2]-y[2])) 表示两个矢量之间的距离。

b.Meanshift聚类：
MeanShift算法是一种在离散数据样本中寻找密度极值的方法。通过概率密度梯度函数估计离散点在各空间维的偏移均值来更新位置,通过不断迭代使得离散点移动到局部高密度值区。
MeanShift定义了一组核函数, 确保离散点与当前聚类中心点的距离不同, 其对新聚类中心偏移向量的贡献亦不同。

详细教程细节可观看视频学习：

Python教程

视频节选自王静老师的Python数据分析-入门案例实战

王静老师：中国科学院博士/国际期刊审稿国家重大项目负责人/国家自然科学基金专家。

课程历经三个月打磨，对于基于位置服务的应用案例进行剖析，通过具体案例结合实际，实现Python学习的从零入门。

学习完整个课程你可以学到：
1.快速的进行python语言的入门，并在使用过程中得到提升
2.python常用库的深入理解
3.机器学习算法原理的讲解及python实现
4.机器学习、python处理轨迹数据的案例应用

下面附全部课程的视频链接，希望对您的学习有用：
https://edu.csdn.net/course/detail/25576

扫码入Python技术交流群，可免费听技术讲座+领学习资料+视频课免费看！