每天一排序：归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序是一种稳定的排序方法。这是百度百科给的解释，需要深入体会。。。记住最后一句话，归并排序是一种稳定的排序方法。

下面说下其他版本的解释：归并排序可以看做是一场比武大会，比武大会需要选拔出最厉害的武术高手，可是参与者众多，总不能让他们去打群架吧？所以擂台赛这样的比武方式出现了。无论参赛者有多少人，主办方都可以让他们两两比试，第一轮的胜者再分成两两一组，继续比试。。。一直到决出冠军为止。

举个例子，有A、B、C、D、E、F、G、H一共8个武术家参考参加比武大会。

第一轮，两两一组，有4名选手胜出（四分之一决赛）

第二轮，两两一组，有两名选手胜出（半决赛）

第三轮，仅剩的两人一组，冠军胜出（总决赛）

这就是擂台赛的流程：先进行两两分组比赛，小组胜出者继续分组比赛，最终选出第一名。归并排序的流程也是类似，但又存在一些不同之处。

归并排序和擂台赛，有什么相同和不同之处呢？让我们以下面这个数组来举例说明：

归并排序就像是组织一场元素之间的“比武大会”，这场比武大会分成两个阶段：

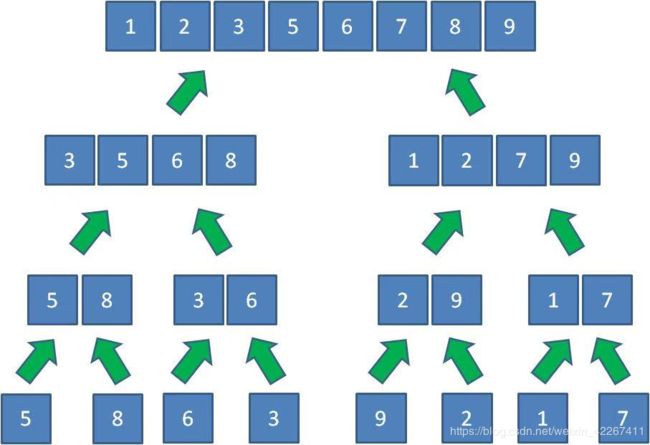
1.分组

假设集合一共有n个元素，算法将会对集合进行逐层的折半分组。

第一层分成两个大组，每组n/2个元素；

第二层分成4个小组，每组n/4个元素；

第三层分成8个更小的组，每组n/8个元素；

......

一直到每组只有一个元素为止。

这样一来，整个数组就分成了一个个小小的“擂台”。

2.归并

既然分了组，接下来就要开始“比武”了。

归并排序和擂台赛有一个很大的不同，就是擂台赛只需要决定谁是老大，而并不关心谁做老二和老三；归并排序的要求复杂一些，需要确定每一个元素的排列位置。

因此，当每个小组内部比较出先后顺序以后，小组之间会展开进一步的比较和排序，合并成一个大组；大组之间继续比较和排序，再合并成更大的组......最终，所有元素合并成了一个有序的集合。

这个比较与合并的过程叫做归并，对应英文单词merge，这正是归并排序名字的由来。

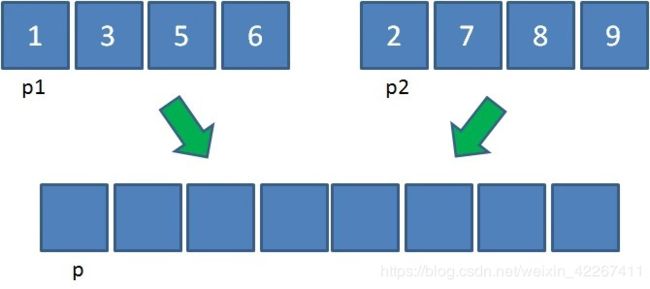
归并操作需要哪三个步骤呢？我们以两个长度为4的集合为例：

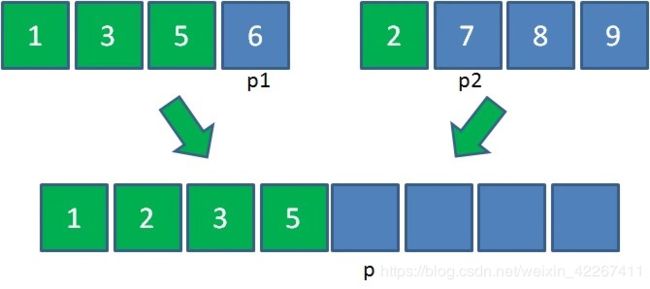
第一步，创建一个额外大集合用于存储归并结果，长度是两个小集合之和。（p1，p2，p是三个辅助指针，用于记录当前操作的位置）

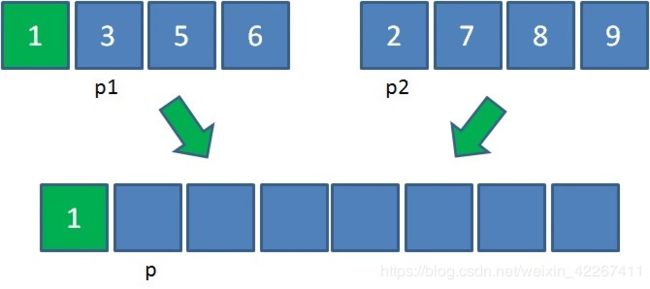
第二步，从左到右逐一比较两个小集合中的元素，把较小的元素优先放入大集合。

由于1<2，所以把元素1放入大集合，p1和p各右移一位：

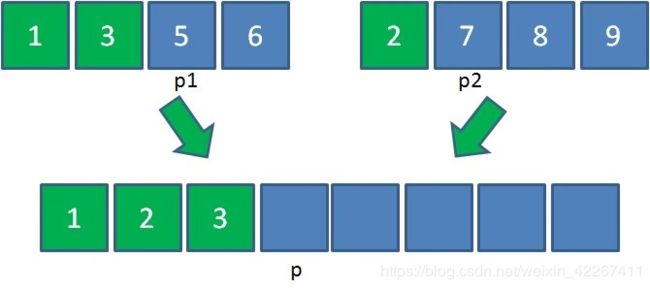
由于2<3，所以把元素2放入大集合，p2和p各右移一位：

由于3<7，所以把元素3放入大集合，p1和p各右移一位：

由于5<7，所以把元素5放入大集合，p1和p各右移一位：

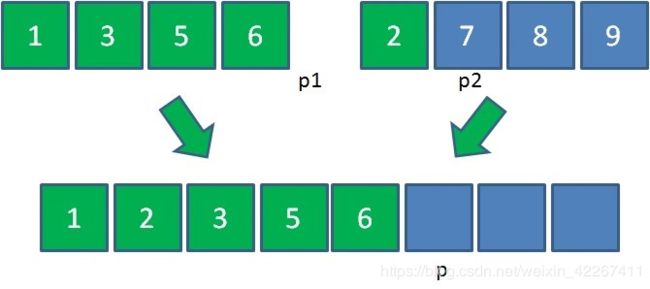
由于6<7，所以把元素6放入大集合，p1和p各右移一位：

此时左侧的小集合已经没有元素可用了。

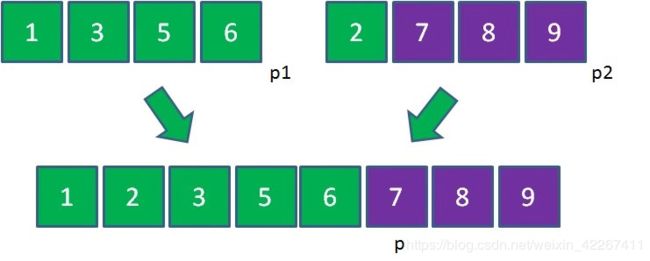
第三步，从另一个还有剩余元素的集合中，把剩余元素按顺序复制到大集合尾部。

这样一来，两个有序的小集合就归并成了一个有序的大集合。

下面看看具体实现代码：

package com.lzy.sort;

/**
 * @Auther: 安静读书
 * @Date: 2019/10/12 06:30
 * @Description:归并排序算法
 */
public class MergeSort {
    public static int [] mergeSort(int[] nums,int l, int h){
        if(l == h)
            return new int[] {nums[l]};
        int mid = l + (h - l)/2;
        int[] leftArr = mergeSort(nums, l , mid);//左有序数组
        int[] rightArr = mergeSort(nums, mid + 1, h);//右有序数组
        int[] newNum = new int[leftArr.length + rightArr.length];//新有序数组

        int m = 0, i = 0, j = 0;
        while (i < leftArr.length && j < rightArr.length){
            newNum[m++] = leftArr[i] < rightArr[j] ? leftArr[i++] : rightArr[j++];
        }
        while (i < leftArr.length)
            newNum[m++] = leftArr[i++];
        while (j < rightArr.length)
            newNum[m++] = rightArr[j++];
        return newNum;
    }

    public static void main(String[] args) {
        int nums[] = new int[]{1,2,5,9,6,4,7,10,8,9};
        int newNums[] = mergeSort(nums,0,nums.length - 1);
        for(int x : newNums){
            System.out.println(x);
        }
    }
}

最后说说归并排序的时间复杂度和空间复杂度：

归并排序把集合一层一层进行拆半分组。如果集合长度是n，那么拆半的层数就是logn，每一层进行归并操作的运算量是n。

所以归并排序的时间复杂度是每一层的运算量乘以层级数，即O(n log n) 。

由于每次归并所创建的额外集合都会随着方法的结束而被释放，因此这部分空间不应该累加计算，单词归并操作开辟的最大空间是n，所以归并排序的空间复杂度是T(n)。

归并排序是稳定的排序方式，两个值相同的元素在归并之后，左侧的元素仍然在左，右侧的元素仍然在右。

Come on！！！