红黑树

参考文献：
http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html
http://blog.csdn.net/iamxiaoguizi/article/details/52080043
http://www.cnblogs.com/yangecnu/p/Introduce-2-3-Search-Tree.html

1.定义性质

•性质 1：每个节点要么是红色，要么是黑色。
•性质 2：根节点永远是黑色的。
•性质 3：所有的叶节点都是空节点（即 null），并且是黑色的。
•性质 4：每个红色节点的两个子节点都是黑色。（从每个叶子到根的路径上不会有两个连续的红色节点）
•性质 5：从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。

2.背景，why red-black tree

（1）普通的二叉查找树
不平衡，导致最低查找速度低
（2）avl树，平衡二叉树
平衡，但是维护平衡性代价高，需要经常进行旋转（如果是进行进行查找，而只有少量的添加，删除，则比较适合）
（3）AVL的扩展，2-3数（非二叉树）
类似于B-树，只是非叶节点至多只有2个节点（当出现不平衡时，调整节点中的关键字个数，如果超过2，则上提+分裂）
相比于二叉树来说，维护平衡简单，但是查找复杂，需要在非叶节点上进行判断，效率低（B树系列一般用于数据库中，数据量大，需要保持较低的树的形态）
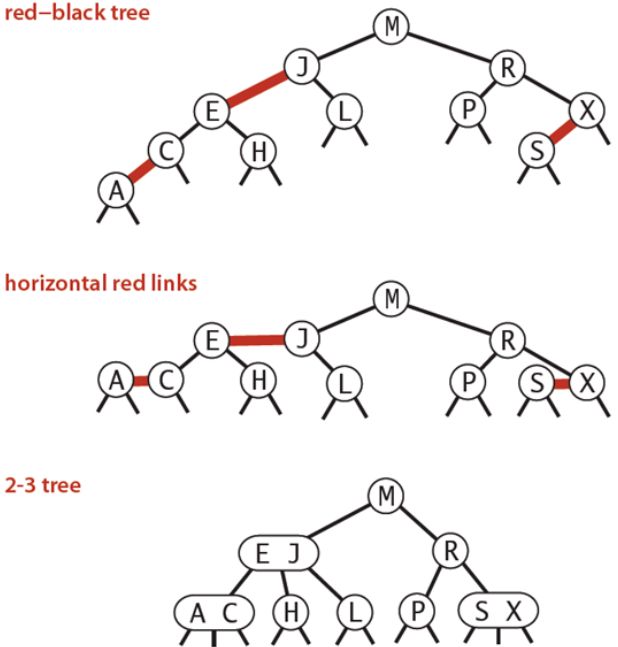
（4）red-black树
改进的2-3树，用颜色来模拟3节点。查找时，和普通的二叉树查找逻辑相同，并且，维护平衡相对于AVL树来说，要简单。
由此我们可以得出结论：对于给定的黑色高度为 N 的红黑树，从根到叶子节点的最短路径长度为 N-1，最长路径长度为 2 * (N-1)。
最长长度不大于2*lgN

3.例子

4. 实现（以java8中Treemap为例）

上面的性质 3 中指定红黑树的每个叶子节点都是空节点，而且并叶子节点都是黑色。但 Java 实现的红黑树将使用 null 来代表空节点，因此遍历红黑树时将看不到黑色的叶子节点，反而看到每个叶子节点都是红色的。
用节点的颜色来表示（从父节点->该节点）连接的颜色(简单的红黑树只需要left ,rigth,color,value 4元组就可以了。这里贴的其他属性是为了配合map的特性添加的。

     static final class Entry<K,V> implements Map.Entry<K,V> {
        K key;
        V value;
        Entry left;
        Entry right;
        Entry parent;
        boolean color = BLACK;

        /**
         * Make a new cell with given key, value, and parent, and with
         * {@code null} child links, and BLACK color.
         */
        Entry(K key, V value, Entry parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }

5. 查找

红黑树是一种特殊的二叉查找树，他的查找方法也和二叉查找树一样，不需要做太多更改。

但是由于红黑树比一般的二叉查找树具有更好的平衡，所以查找起来更快。

    final Entry getEntry(Object key) 
    {//查找以key为键的条目
        // Offload comparator-based version for sake of performance
        if (comparator != null)
            return getEntryUsingComparator(key);
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparablesuper K> k = (Comparablesuper K>) key;

        Entry p = root;
        while (p != null) {
            int cmp = k.compareTo(p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
        return null;
    }

6. 插入

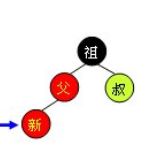
在讨论红黑树的插入操作之前必须要明白，任何一个即将插入的新结点的初始颜色都为红色。这一点很容易理解，因为插入黑点会增加某条路径上黑结点的数目，从而导致整棵树黑高度的不平衡。但如果新结点父结点为红色时（如图2所示），将会违返红黑树性质：一条路径上不能出现相邻的两个红色结点。这时就需要通过一系列操作来使红黑树保持平衡。

步骤：先找，如果找到，则更新value，没有找到（因为遍历到了页节点，之后都没有节点了），则在最后一个遍历到的节点上插入，然后调整树的形态，使保持红黑树的形态。

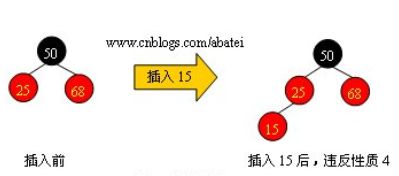
为了清楚地表示插入操作以下在结点中使用“新”字表示一个新插入的结点；使用“父”字表示新插入点的父结点；使用“叔”字表示“父”结点的兄弟结点；使用“祖”字表示“父”结点的父结点。插入操作分为以下几种情况：
1、黑父
(如果新点的父结点为黑色结点，那么插入一个红点将不会影响红黑树的平衡，此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见，从而使红黑树需要旋转的几率相对AVL树来说会少一些)

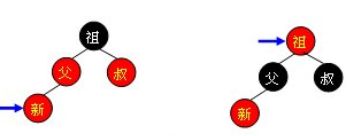
2．红父
如果新点的父结点为红色，这时就需要进行一系列操作以保证整棵树红黑性质。如图3所示，由于父结点为红色，此时可以判定，祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作，而每次进行不平衡判断的起始点（我们可将其视为新点）都不一样。所以我们在此使用一个蓝色箭头指向这个起始点，并称之为判定点。

2．1黑叔
当叔父结点为红色时，如图4所示，无需进行旋转操作，只要将父和叔结点变为黑色，将祖父结点变为红色即可。但由于祖父结点的父结点有可能为红色，从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上进行平衡操作。

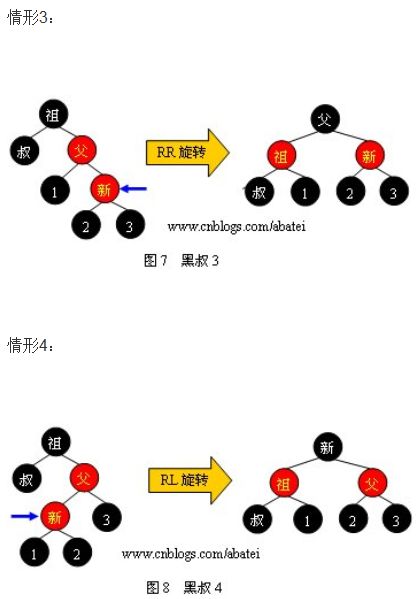
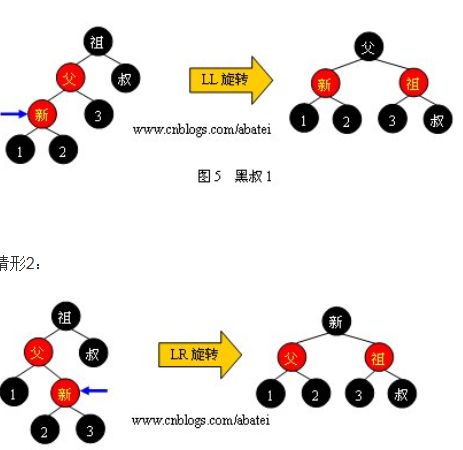
2．2黑叔
当叔父结点为黑色时，需要进行旋转，以下图示了所有的旋转可能

  public V put(K key, V value) 
    {
        Entry t = root;
        if (t == null) //当前树为空树，什么都不用做，树根为black,默认的
        {
            compare(key, key); // type (and possibly null) check

            root = new Entry<>(key, value, null);
            size = 1;
            modCount++;
            return null;
        }
        int cmp;
        Entry parent;
        // split comparator and comparable paths
        Comparator super K> cpr = comparator;
        if (cpr != null) 
        {
            do {
                parent = t;
                cmp = cpr.compare(key, t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        else 
        {
            if (key == null)
                throw new NullPointerException();
            @SuppressWarnings("unchecked")
                Comparable super K> k = (Comparable super K>) key;
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
          //上面的if-else里面的内容都是一样的，区别在于创建Tree的时候有没有指定comparator（没有的话，用的是默认的），这两段的逻辑都是一样的，先找，找到就返回，没有找到，会进行插入（保存找到的最后一个节点）

        //如果之前没有key对应的条目，则要进行插入，parent是上面到达的最后 一个叶子节点
        Entry e = new Entry<>(key, value, parent);
        if (cmp < 0)
            parent.left = e;
        else
            parent.right = e;
        //调整左右，使得平衡
        fixAfterInsertion(e);
        size++;
        modCount++;
        return null;
    }

 /** From CLR */
    //调整节点的颜色，相比AVL树来说，不需要多次检测树的节点的平衡度。另外，由于上提时，只需要变更颜色即可
    //减少了树的形状变更的次数。
    private void fixAfterInsertion(Entry x) 
    {  //X为新插入的节点（因为之前的树的形态都保持在红黑树的形态
        //，则每次插入，只要保证X相关的节点也是良好的颜色，即可）
        x.color = RED;//新插入的节点初始颜色都是红的
        while (x != null && x != root && x.parent.color == RED) 
        {   //求当前节点的父节点（为什么不直接x.parent?反正x!=null）
            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) 
            {  //父节点是"祖父"的左孩子
                Entry y = rightOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) //叔叔也是红色的
                {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    //颜色上提，然后重新判断上提后的祖父是否需要改变
                    x = parentOf(parentOf(x));
                    //颜色上提时，X才会“向前”移动，跑到下一个红色的要检查的节点上去
                } 
                else 
                {//只有两个连续的父子边是红的，不满足上提的条件（叔叔不是红色的）
                    if (x == rightOf(parentOf(x))) 
                    {//左旋，将p的右孩子向上调整，使得右孩子成为父节点
                        x = parentOf(x);
                        rotateLeft(x);
                    }
                    //并没有一次性的将x,p旋转并颜色翻转上提，这里只是将p变成了黑色，
                    //然后p有了连个红色的子节点（X、PP），颜色上提在下一次的检测中完成
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateRight(parentOf(parentOf(x)));
                }
            } 
            else  //父节点是"祖父"的右孩子
            {
                Entry y = leftOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) 
                {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else 
                {
                    if (x == leftOf(parentOf(x))) 
                    {
                        x = parentOf(x);
                        rotateRight(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateLeft(parentOf(parentOf(x)));
                }
            }
        }
        root.color = BLACK;
    }

7.

8.

9.