Java数据结构之二叉平衡树

首先二叉平衡树依然是一课二叉搜索树，关于二叉搜索树以及其平均查找时间的分析，可以见关于二叉查找树的平均查找时间的问题这一篇。我可能写得不太好，所以最好还是参考一些教材，教材的描述通常会更为严谨，博客比较适合临阵磨枪。通常我们认为二叉搜索树的平均查找时间为O(logN)，但不排除极端状况下二叉查找树会成为链表，那么此时，查找时间就会上升到O(N)，这有悖于我们使用二叉查找树的初衷，好在我们遭遇到的问题早有前辈给出了解决方案，也就是平衡树，它是Adelson-Velskii和Landis于1962年首先提出的，所以又称为AVL树，当然我们还要记住，平衡树有诸多实现方式，AVL树只是其中的一种。

AVL树的定义

AVL树的特性是：任意结点其左子树与右子树的的高度最多差为1，空树为-1，这个差值也称为平衡因子。

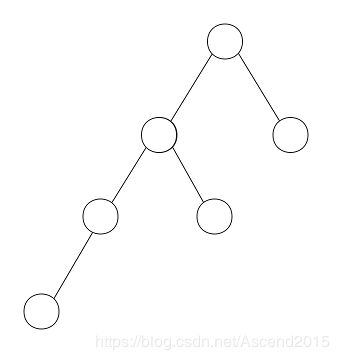
以上是失衡二叉树

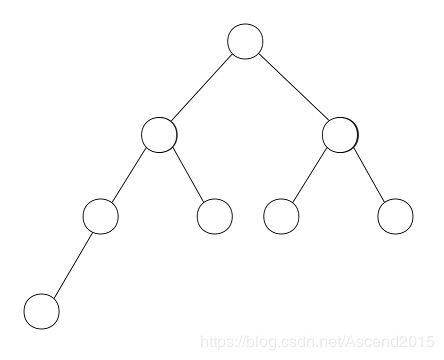
以上是平衡二叉树

妈的随手画的图太尼玛丑了，但是图片不是重点，反正意思到了就行。

平衡二叉树的实现

假设失衡的结点为x，那么首先我们需要弄清楚哪些操作可能会导致树的失衡：

1. 在x的左孩子结点的左子树上插入元素；
2. 在x的左孩子结点的右子树上插入元素；
3. 在x的右孩子结点的左子树上插入元素；
4. 在x的右孩子结点的右子树上插入元素；

如图所示，这个是维基百科上的，总算比我自己画的好太多了。

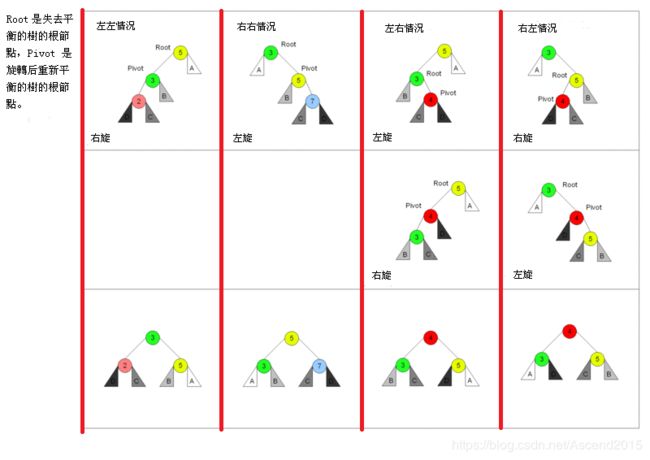
二叉树的平衡通过旋转的操作来调整，所以我们有必要先了解旋转操作，旋转分为单选和双旋，二叉树的平衡通过旋转的操作来调整，所以我们有必要先了解旋转操作，旋转分为单选和双旋。上述情况中1和4是对称的，可以通过单旋转来解决，2和3是对称的，通过双旋来解决。

结点实现

public class TreeNode{
	private TreeNode left;
	private TreeNode right;
	private T data;
	//与普通的二叉搜索树不同，这里添加了一个height高度属性
	private int height;
	public TreeNode(T data){
		TreeNode(null,null,data);
	}
	public TreeNode(TreeNode left,TreeNode right,T data){
		TreeNode(left,right,data,0);
	}
	public TreeNode(TreeNode left,TreeNode right,T data,int height){
		this.left=left;
		this.right=right;
		this.data=data;
		this.height=height;
	}
}

高度：当前结点到叶子结点的最长路径。
深度：当前结点到根节点的最长路径。

单旋双旋

首先对于情况1，LL（左左）情况，需要通过单右旋来解决

private TreeNode singleRightRotate(TreeNode x){
	//将x的左子树赋值给y
	TreeNode y=x.left;
	//y的右子树变为x的左子树
	x.left=y.right;
	//x成为y的右子树
	y.right=x;
	//重新计算x、y的高度
	x.height=Math.max(height(x.right),height(x.left))+1;
	y.height=Math.max(height(y.right),height(y.left))+1;
	return y;
}

对于情况4，RR（右右）情况，需要通过单左旋来解决

private TreeNode singleRightRotate(TreeNode x){
	//将x的右子树赋值给y
	TreeNode y=x.right;
	//y的左子树变为x的右子树
	x.right=y.left;
	//x成为y的左子树
	y.left=x;
	//重新计算x、y的高度
	x.height=Math.max(height(x.right),height(x.left))+1;
	y.height=Math.max(height(y.right),height(y.left))+1;
	return y;

然后对于情况2/3，单旋无法解决，而必须采用双旋的方式解决。原因在于新插入的D结点深度太深了，此时无论是左旋还是右旋都无法满足调整后平衡因子<=1。
我们先解决情况2的问题，此时对x进行旋转已经是无效的了，我们考虑：

1. 对x的左孩子y进行左旋，完成之后它的右孩子z成为它的父亲节点，x成为它的祖父节点；
2. 对z进行右旋，完成后y成为它的左子树，x成为它的右子树

代码实现

private TreeNode doubleRotateLeft(TreeNode x){
	x.left=singleRotateLeft(x.left);
	return singleRotateRight(x);
}

同理它的对称情况3

private TreeNode doubleRotateRight(TreeNode x){
	x.right=singleRotateLeft(x.right);
	return singleRotateLeft(x);
}

二叉平衡树的基本操作

插入操作

public void insert(T data){
	if(data==null)
		throw new RuntimeException("data cannot be null");
	this.root=insert(data,root);
}

public TreeNode insert(T data,TreeNode node){
	//没有孩子节点，创建新节点插入
	if(node==null)
		node=new TreeNode(data);
	else if(data.compareTo(node.data)<0){
		//向左子树查找插入位置
		node.left=insert(data,node.left);
		//插入后需要计算子树的高度，等于2则需要调整恢复平衡，由于是插入左子树，因此左边一定高于右边
		if(height(node.left)-height(node.right)==2){
			//判断是插入左孩子还是右孩子
			if(data.compareTo(node.left.data)<0)
				//进行右旋
				singleRotateRight(node);
			else
				//左右旋转
				doubleRotateLeft(node);
		}
	}else if(data.compareTo(node.data)>0){
		//向右子树查找插入位置
		node.right=insert(data,node.right);
		if(height(node.left)-height(node.right)==2){
			//判断是插入左孩子还是右孩子
			if(data.compareTo(node.left.data)<0)
				//进行左旋
				singleRotateLeft(node);
			else
				//右左旋转
				doubleRotateRight(node);
		}
	}else{
	;
	}
	node.height=Math.mat(height(node.left),height(node.right))+1;
	return node;
}

删除操作

public void remove(T data){
	if(data==null)
		throw new RuntimeException("data cannot be null");
		this.root=remove(data,root);
}

public TreeNode remove(T data,TreeNode node){
	if(node==null)
		return null;
	int result=data.compareTo(node.data);
	//从左子树查找需要删除的节点
	if(result<0){
		node.left=remove(data,node.left);
		//检测是否平衡
		if(height(node.right)-height(node.left)==2){
			//不平衡
			TreeNode curr=node.right;
			//判断需要哪种旋转
			if(height(curr.left)>height(curr.right))
				//左旋
				singleRotateLeft(curr);
			else
				//左右双旋
				doubleRotateleft(curr);
		}
	}else(result>0){
		//向右子树查找
		node.right=remove(data,node.right);
		//检测平衡
		if(height(node.left)-height(node.right)==2){
			TreeNode curr=node.left;
			//判断需要哪一种旋转
			if(height(node.right)>height(node.left))
				//左旋
				singleRotateRight(curr);
			else
				//右左双旋
				doubleRotateRight(curr);
		}
	}
	//找到要删除的节点且该节点拥有两个不为空的子节点
	else if(node.left!=null&&node.right!=null){
		//寻找替换节点
		node.data=findMin(node.right).data;
		//移除用于替换的节点
		node.right=remove(node.data,node.right);
	}
	//只有一个子节点或者要删除的就是叶子节点
	else{
		node=(node.left!=null)?node.left:node.right;
	}
	//更新高度
	if(node!=null)
		node.height=Math.max(height(node.left),height(node.right))+1;
	return node;
}

//TODO