Gartner力推的“百页机器学习书”,“舒服”搞定概念+代码(附下载)
大数据文摘出品
作者:曹培信
去年十二月,一本名为《TheHundred-Page Machine LearningBook》的机器学习教程迅速走火,它由Gartner公司机器学习团队负责人、人工智能博士AndriyBurkov撰写,这本书如标题所言,去除封面目录才128页,但是却包含了机器学习50多年以来有实用价值的各种材料。
作者介绍说:“机器学习的初学者将在本书中获得足够的细节,可以很‘舒服’地理解书的内容;有经验的实践者可以使用这本书作为进一步自我完善的指南。”
这本书讲了什么?
这本书一共分为两大部分,在介绍了机器学习的基本知识之后,本书首先用8章讲了SupervisedLearning(监督式学习),而后用3章介绍了UnsupervisedLearning(非监督式学习)和其他学习方式。
具体目录如下图所示:
示例代码已经开源
如今,这本书所有涉及到的项目代码都在GitHub上开源啦!
也就是说,大家可以一边看书学习,一边用开源的代码进行实验了。不得不说,这些代码对新手真的太友好了,内容特别详细。
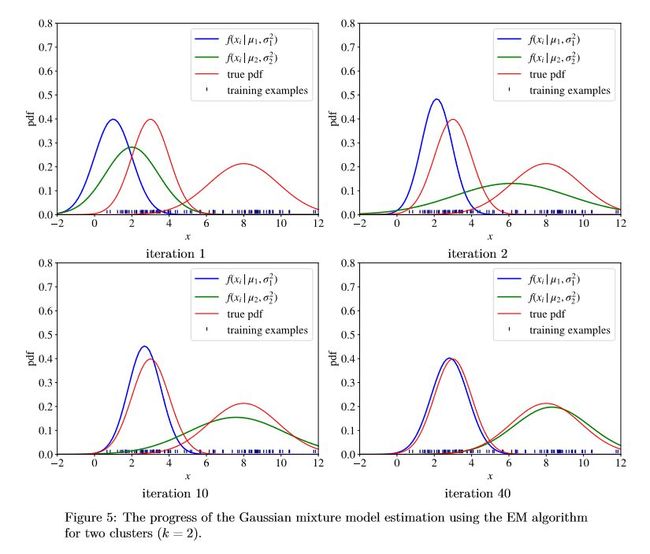
比如多元高斯分布(GaussianMixture Model GMM)这个内容,作者在书的9.2.4进行了详细的讲解:
在GitHub上也有对应的详细代码:
importnumpy as npimportscipy as spimportmatplotlibimportmatplotlib.pyplot as pltimportmathfromsklearn.neighbors import KernelDensityimportscipy.integrate as integratefromsklearn.kernel_ridge import KernelRidgematplotlib.rcParams['mathtext.fontset']= 'stix'matplotlib.rcParams['font.family']= 'STIXGeneral'matplotlib.rcParams.update({'font.size':18})mu1,sigma1 = 3.0, 1.0mu2,sigma2 = 8.0, 3.5defsample_points():s1= np.random.normal(mu1, math.sqrt(sigma1), 50)s2= np.random.normal(mu2, math.sqrt(sigma2), 50)return list(s1) + list(s2)defcompute_bi(mu1local, sigma1local, mu2local, sigma2local, phi1local,phi2local):bis= []forxi in x:bis.append((sp.stats.norm.pdf(xi, mu1local, math.sqrt(sigma1local)) *phi1local)/(sp.stats.norm.pdf(xi, mu1local, math.sqrt(sigma1local)) *phi1local + sp.stats.norm.pdf(xi, mu2local, math.sqrt(sigma2local)) *phi2local))return bis#generate points used to plotx_plot= np.linspace(-2, 12, 100)#generate points and keep a subset of themx =sample_points()colors= ['red', 'blue', 'orange', 'green']lw = 2mu1_estimate= 1.0mu2_estimate= 2.0sigma1_estimate= 1.0sigma2_estimate= 2.0phi1_estimate= 0.5phi2_estimate= 0.5count =0whileTrue:plt.figure(count)axes = plt.gca()axes.set_xlim([-2,12])axes.set_ylim([0,0.8])plt.xlabel("$x$")plt.ylabel("pdf")plt.scatter(x, [0.005] * len(x), color='navy', s=30, marker=2,label="training examples")plt.plot(x_plot, [sp.stats.norm.pdf(xp, mu1_estimate,math.sqrt(sigma1_estimate)) for xp in x_plot], color=colors[1],linewidth=lw, label="$f(x_i \\mid \\mu_1 ,\\sigma_1^2)$")plt.plot(x_plot, [sp.stats.norm.pdf(xp, mu2_estimate,math.sqrt(sigma2_estimate)) for xp in x_plot], color=colors[3],linewidth=lw, label="$f(x_i \\mid \\mu_2 ,\\sigma_2^2)$")plt.plot(x_plot, [sp.stats.norm.pdf(xp, mu1, math.sqrt(sigma1)) forxp in x_plot], color=colors[0], label="true pdf")plt.plot(x_plot, [sp.stats.norm.pdf(xp, mu2, math.sqrt(sigma2)) forxp in x_plot], color=colors[0])plt.legend(loc='upper right')plt.tight_layout()fig1 = plt.gcf()fig1.subplots_adjust(top = 0.98, bottom = 0.1, right = 0.98, left =0.08, hspace = 0, wspace = 0)fig1.savefig('../../Illustrations/gaussian-mixture-model-' +str(count) + '.eps', format='eps', dpi=1000, bbox_inches = 'tight',pad_inches = 0)fig1.savefig('../../Illustrations/gaussian-mixture-model-' +str(count) + '.pdf', format='pdf', dpi=1000, bbox_inches = 'tight',pad_inches = 0)fig1.savefig('../../Illustrations/gaussian-mixture-model-' +str(count) + '.png', dpi=1000, bbox_inches = 'tight', pad_inches = 0)#plt.show()bis1 = compute_bi(mu1_estimate, sigma1_estimate, mu2_estimate,sigma2_estimate, phi1_estimate, phi2_estimate)bis2 = compute_bi(mu2_estimate, sigma2_estimate, mu1_estimate,sigma1_estimate, phi2_estimate, phi1_estimate)#print bis1[:5]#print bis2[:5]mu1_estimate = sum([bis1[i] * x[i] for i in range(len(x))]) /sum([bis1[i] for i in range(len(x))])mu2_estimate = sum([bis2[i] * x[i] for i in range(len(x))]) /sum([bis2[i] for i in range(len(x))])sigma1_estimate = sum([bis1[i] * (x[i] - mu1_estimate)**2 for i inrange(len(x))]) / sum([bis1[i] for i in range(len(x))])sigma2_estimate = sum([bis2[i] * (x[i] - mu2_estimate)**2 for i inrange(len(x))]) / sum([bis2[i] for i in range(len(x))])#print mu1_estimate, mu2_estimate#print sigma1_estimate, sigma2_estimatephi1_estimate = sum([bis1[i] for i in range(len(x))])/float(len(x))phi2_estimate = 1.0 - phi1_estimateprint phi1_estimatecount += 1plt.close(count)ifcount > 50:break
如何获得书和代码
书的链接:
http://themlbook.com/wiki/doku.php?id=start
代码链接:
https://github.com/aburkov/theMLbook
当然,文摘菌也帮大家下载并整理好了书和代码,后台回复“100页”就可以获得啦,赶紧开始学习起来吧!