目标跟踪综述:《Machine Learning Methods for Solving Assignment Problems in Multi-Target Tracking》
文章目录
- 引言
- 问题表达
- 2.1 Linear Assignment
- 2.2 Multidimensional Assignment
- 2.3 Assignment Costs
- 2.3.1 Kinematic Costs
- 优化
- 3.1 最大权重独立集问题
- 3.2 贪婪随机搜索
- 3.2.1 TOMHT Framework
- 3.2.2 GRASP for the Hypothesis Enumeration
- 搜索算法
- 可行解的构造
- 本地搜索
- 3.3 网络流方法
引言
多目标跟踪的主要任务是给定一个图像序列,找到图像序列中运动的物体,并将不同帧的物体一一对应,给出不同物体的运动轨迹。应用场景包括行人检测,交通监控,自动驾驶等。
多目标跟踪问题在关键在于数据关联(data association)和轨迹间关联问题(track-to-track association)。数据关联指的是对一组新检测结果与已存在目标轨迹进行匹配。当有多个传感器时,需要处理轨迹间关联问题。我们需要对来自不同传感器的相同目标进行匹配。
问题表达
2.1 Linear Assignment
问题描述:在 k k k时刻有 m m m个已知轨迹(track)和 n n n个检测结果(detection, measurement)其中 k = 1 , . . . , T k = 1,...,T k=1,...,T。假设有一个矩阵 C k ∈ R m × n C_k \in R^{m \times n} Ck∈Rm×n,元素 c k i j ∈ C c_k^{ij} \in C ckij∈C表示在 k k k时刻将第 j j j个measurement与第 i i i个track进行匹配的成本。用二元变量 x i j ∈ { 0 , 1 } x^{ij} \in \{0,1\} xij∈{0,1}表示是否分配。问题的目标是找到最优匹配使总成本最小。
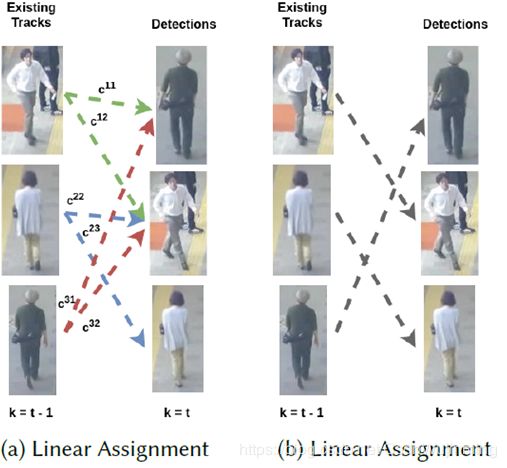
min x ∈ X ∑ i = 1 m ∑ j = 1 n c k i j x i j \min_{x \in X}\sum_{i=1}^m\sum_{j=1}^nc_k^{ij}x^{ij} x∈Xmini=1∑mj=1∑nckijxij
with constraints
∑ i = 1 m x i j , j = 1 , . . . , n \sum_{i=1}^mx^{ij}, j = 1,...,n i=1∑mxij,j=1,...,n
∑ j = 1 n x i j , j = 1 , . . . , m \sum_{j=1}^nx^{ij}, j = 1,...,m j=1∑nxij,j=1,...,m
约束条件说明measurement与track间只能唯一匹配。
最常用的算法是Hungarian (匈牙利算法),复杂度为 O ( n 3 ) O(n^3) O(n3)。对于目标跟踪问题,LA只考虑前一时刻的measurement数据关联,优点是速度快,可实现实时跟踪算法,问题是对于堵塞,误检,漏检等情况表现不行。一个可行的方法是设置时间上的滑动窗口,关联时延时决策,使用多个时刻的measurement信息。问题变换为下面要说明的问题。
2.2 Multidimensional Assignment

问题描述: T T T为时间窗口, Z T = { Z 1 , Z 2 , . . . . , Z T } Z^T = \{Z_1,Z_2,....,Z_T\} ZT={Z1,Z2,....,ZT}为不同时刻的measurements组成的集合,目标是找到一个该集合的划分使总成本最小。
M k M_k Mk: k k k时刻mesurements总个数
c i 1 , i 2 , . . . , i T c_{i_1,i_2,...,i_T} ci1,i2,...,iT:不同时刻的measurements串成一条轨迹的成本
ρ \rho ρ:相应二元决策变量
注意:其它论文中 i 1 , i 2 , . . . , i T {i_1,i_2,...,i_T} i1,i2,...,iT从0开始,为0时说明选择的measurement为假。因为个个时刻的measurement个数可能不等。
说明一下第一个约束等式,等式中 i 1 i_1 i1不变,指第1个时刻时的任意measurement都只与一个track匹配。其它约束等式相同。
2.3 Assignment Costs
计算Cost 矩阵
2.3.1 Kinematic Costs
基于概率计算cost


 串成真轨迹和假轨迹概率之比。检测的measurement不一定为真,存在一个真假的概率分布,分子是measurement为真且串成轨迹的概率,分母是假轨迹概率。
串成真轨迹和假轨迹概率之比。检测的measurement不一定为真,存在一个真假的概率分布,分子是measurement为真且串成轨迹的概率,分母是假轨迹概率。
![]() :第k个时刻目标状态的measurement为 z k i z^i_k zki的概率
:第k个时刻目标状态的measurement为 z k i z^i_k zki的概率
![]() :第j个轨迹k时刻的状态为 x k x_k xk的概率。
:第j个轨迹k时刻的状态为 x k x_k xk的概率。
优化
由于该问题为NP-Hard问题,我们需要设计算法近似求解最优值。
3.1 最大权重独立集问题
独立集指图顶点的一个子集,满足任意两点间没有边连接,两个问题等价,不过要将cost转换为track score。证明可查阅《The Maximum Weight Independent Set Problem for Data Association in Multiple》。


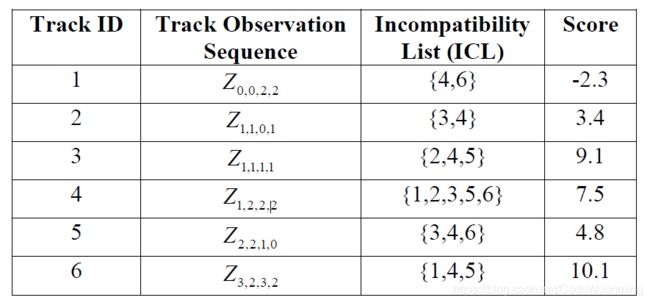 Z 0 , 0 , 2 , 2 Z_{0,0,2,2} Z0,0,2,2说明四个时刻分别将1时刻第0个measurement,2时刻第0个measurement。。。串成一个轨迹,与第4个轨迹后两个选择冲突,也与6最后一个冲突。
Z 0 , 0 , 2 , 2 Z_{0,0,2,2} Z0,0,2,2说明四个时刻分别将1时刻第0个measurement,2时刻第0个measurement。。。串成一个轨迹,与第4个轨迹后两个选择冲突,也与6最后一个冲突。
3.2 贪婪随机搜索
参考论文《Multiple object video tracking using GRASP-MHT》。
3.2.1 TOMHT Framework
记k时的measurements为 Z ( k ) = { z i k } i = 0 M k , k = 1 , 2 , . . . , N , N Z(k) = \{z_i^k\}^{M_k}_{i=0}, k = 1,2,...,N, N Z(k)={zik}i=0Mk,k=1,2,...,N,N为扫描次数或滑动窗口大小, z i k z_i^k zik为k时第 i i i个measurement, z 0 k z_0^k z0k记为可能的漏检。一个track hypothesis 轨迹假设由一组mesurements组成:
T j k = ( z j 1 1 , z j 2 2 , . . . , z j n n , . . . , z j k k ) , j n ∈ Z ( n ) T_j^k = (z^1_{j_1},z^2_{j_2},...,z^n_{j_n},...,z^k_{j_k}),j_n \in Z(n) Tjk=(zj11,zj22,...,zjnn,...,zjkk),jn∈Z(n)如果track T j k − 1 T_j^{k-1} Tjk−1与measuremetn z i k z_i^k zik关联,则轨迹得分 track score 的增量为
Δ L i j i = { l o g ( p ( z i k ∣ T j k − 1 ) P D λ ϕ + λ υ ) i ≠ 0 l o g ( 1 − P D ) i = 0 \Delta L^i_{ij} = \begin{cases} log(\frac{p(z_i^k|T_j^{k-1})P_D}{\lambda_{\phi}+\lambda_{\upsilon}}) & i \neq 0 \\ log(1-P_D) & i = 0 \end{cases} ΔLiji={log(λϕ+λυp(zik∣Tjk−1)PD)log(1−PD)i̸=0i=0

则 T j k T^k_j Tjk的track sorce 为增量总和:
L ( T j k ) = ∑ i = j 1 j k Δ L i j k L(T^k_j)=\sum_{i=j_1}^{j_k}\Delta L^k_{ij} L(Tjk)=i=j1∑jkΔLijk
当两个track不共享正确检测则它们互相兼容。一个全局假设global hypothesis 为互相兼容的track组成的集合。则假设 H i k H_i^k Hik的score为其中包含的所有tracks scores之和:
L ( H i k ) = ∑ T j k ∈ H i k L ( T j k ) L(H_i^k)=\sum_{T^k_j \in H_i^k}L(T^k_j) L(Hik)=Tjk∈Hik∑L(Tjk)
在枚举所有 J J J个假设后,特定假设发生概率为:
P { H i k } = exp ( L ( H i k ) ) 1 + ∑ j = 1 J exp ( L ( H i k ) ) P\{H^k_i\} = \frac{\exp(L(H^k_i))}{1+\sum_{j=1}^J\exp(L(H^k_i))} P{Hik}=1+∑j=1Jexp(L(Hik))exp(L(Hik))
track T j k T^k_j Tjk的概率为:
P { T j k } = ∑ T j k ∈ H i k P { H i k } P\{T^k_j\}=\sum_{T^k_j \in H_i^k}P\{H^k_i\} P{Tjk}=Tjk∈Hik∑P{Hik}
计算复杂度太高:
Gate 方法,只考虑满足不等式的measurement
[ z i k − z ^ j k ∣ k − 1 ] T S − 1 [ z i k − z ^ j k ∣ k − 1 ] ≤ η 2 [z^k_i - \widehat{z}_j^{k|k-1}]^TS^{-1}[z^k_i - \widehat{z}_j^{k|k-1}] \leq \eta^2 [zik−z jk∣k−1]TS−1[zik−z jk∣k−1]≤η2
z ^ j k ∣ k − 1 \widehat{z}_j^{k|k-1} z jk∣k−1为先验预测, S S S为 [ z i k − z ^ j k ∣ k − 1 ] [z^k_i - \widehat{z}_j^{k|k-1}] [zik−z jk∣k−1]的协方差。
3.2.2 GRASP for the Hypothesis Enumeration
在有限次数计算内找出次优解,计算最大权重独立集问题。
搜索算法
可行解的构造
将图顶点按贪心策略排序:greedy function

N + ( v i ) N^+(v_i) N+(vi)为与 v i v_i vi相邻的点和自己本身组成的集合,每次贪心选点时维护一个候选列表condidate list 满足条件:
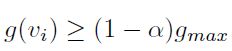
g m a x g_{max} gmax为剩余点的greed function最大值。在初始化选点是,先排序
![]()
选择一对不相连且greedy function 值之和最大的顶点对,初始化后从候选列表中随机抽取一个顶点。


本地搜索
无向图的最大团=该补图的最大独立集
3.3 网络流方法
参考论文《Global Data Association for Multi-Object Tracking Using Network Flows》,《Multi-target Tracking by Lagrangian Relaxation to Min-Cost Network Flow》



