【论文-完整空间多任务模型】Entire Space Multi-Task Model

转载请注明出处：http://blog.csdn.net/gamer_gyt
博主微博：http://weibo.com/234654758
Github：https://github.com/thinkgamer
公众号：搜索与推荐Wiki
个人网站：http://thinkgamer.github.io

---

• 论文：Entire Space Multi-Task Model: An Effective Approach for
  Estimating Post-Click Conversion Rate（CVR预估新思路：完整空间多任务模型）
• 地址：https://arxiv.org/pdf/1804.07931.pdf

---

背景

CVR预估在工业界（比如推荐系统，广告系统）应用非常广泛，常规的CVR模型结合了深度学习方法并取得了不错的效果。然而在实际的应用中也会有一些问题，比如：使用有点击的样本进行模型的训练然后在整个样本集中进行应用，这样会引起样本偏差。此外，还存在极端的数据稀疏问题，从而使得模型训练变得更加困难。

基于用户行为数据（比如展示->点击->转化），论文从一个新的视角来训练CVR模型。ESMM（完整空间多任务模型）解决了两大问题：

• 直接在整个样本空间上进行建模
• 采用特征表示学习策略

基于淘宝推荐系统的日志，该模型的表现优于其竞争模型，论文也会公开一部分抽样数据集用来支持CVR模型的研究。

介绍

CVR预测对于在线排序（例如广告和推荐）是很必要的，例如预测广告的点击，指定一个合适的价格，可以让广告方和平台方达到双赢。同样对于推荐系统而言，平衡用户的点击和购买也是很重要的。

通常来讲，传统的CVR模型采用了和CTR类似的方法去做，例如流行的深度神经网络。然而依旧存在一些挑战，论文里总结了两点：

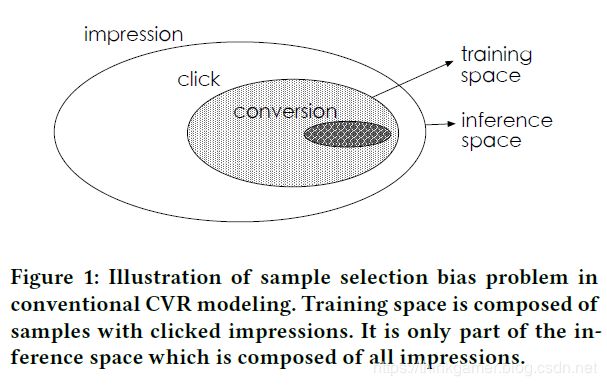
• SSB：smaple selection bias（样本偏差）
• DS：Data sparsity（数据稀疏）

如上图中，曝光展示的样本是很大的， 用户有行为的物品只是其中的一小部分，用户进行了转化的物品又只是有行为物品的一部分，这样在使用用户有行为的物品作为训练数据训练模型，然后应用到整个样本空间内就会产生样本偏差的问题。

论文中也列举了一些已有成果来解决SSB和DS问题的，但都不理想。所以才有了这篇论文，通过利用用户的行为序列，提出了一种新颖的算法（ESMM）来同时解决SSB和DS的问题。

在ESMM模型，分为了两部分模型分别是CTR和CTCVR，用来代替直接训练一个CVR模型，ESMM模型将pCVR视作中间变量，其和pCTR的乘积等于pCTCVR。pCTCVR和pCTR可以在整个样本空间内进行训练。这样样本偏差的问题就能被解决了，另外，CVR和CTR的模型参数是共享的，这样CVR就会有更多的样本，这种参数转换的方法能够有效的解决DS问题。

MSSE

假设数据集形式为：
$$S=\left\{(x_i,y_i->z_i)\right\}|(i\in N)$$
其中：

• x：特征（高维的特征向量，eg:user field,item field等）
• y/z：二分类的label标签（y=1 表示点击，z=1表示转化）
• N：样本数

CVR模型预估可能性的表示为：pCVR=p(z=1 | y=1,x)，两个相关的概率值是：pCTR和pCTCVR，其关系为：
$$\begin{gathered} pCTCVR=pCTR\ast pCVR \\ p(y=1,z=1|x)=p(y=1|x)\ast p(z=1|y=1,x) \end{gathered}$$

常见基于深度学习模型在CVR模型上已经取得了不错的效果，其中的大多数类似于上图中的左侧部分这样的词嵌入和前馈神经网络。

CVR模型预估的是点击转化率（p(z=1|y=1,x=1)），训练模型的样本是基于点击数据的，即：
$$Sc=(x_j,z_j)|y_j=1(j\in M)$$
S_c是整个样本空间S的子集，M是样本空间中点击样本数，点击且未转化的是负样本，点击且转化的为正样本。下面具体解释喜爱SSB问题和DS问题。

• SSB问题

传统的CVR模型实际上是通过引入了特征空间X_c做了一个假设：
$$p(z=1|y=1,x)\approx q(z=1|x_c)$$
x_c 属于X_c，表示（x=x_c,y=1）,这种情况下，q(z=1|x_c)是基于有点击行为的样本空间（S_c）进行训练的，然而在线预估时是针对所有的样本（S）进行计算的，因为S_c是S的一个很小的子集，所以具有很大的随机性，这就可能带来样本偏差和影响模型的泛化能力。

• DS问题

推荐系统展现给用户的商品数量要远远大于被用户点击的商品数量，同时有点击行为的用户也仅仅只占所有用户的一小部分，因此有点击行为的样本空间 S_c相对于整个样本空间S来说是很小，通常来讲，量级要小1-3个数量级。

如下表所示，在淘宝公开的训练数据集上，S_c只占整个样本空间S的4%。这就是所谓的训练数据稀疏的问题，高度稀疏的训练数据使得模型的学习变得相当困难。

除此之外，CVR还存在一个延迟反馈问题，但不在本文的讨论范围内。ESSM模型的结构如Figure2所示，CTR和CVR作为基础模型，拥有相同的结构。

• 在整个样本空间建模

pCVR = pCTCVR / pCTR：
$$p(z=1|y=1,x)=\frac{p(y=1,z=1|x)}{p(y=1|x)}$$
上述公式告诉我们，可以在整个样本空间上进行模型训练，继而解决样本稀疏性的问题。这里可以单独的训练CTR和CTCVR模型，继而通过除法得到CVR。然而CTR一般很小，除法容易引起数值不稳定，ESMM通过乘法公式来避免这种情况。在ESSM中，pCVR只是一个中间变量，pCTR和pCTCVR才是主要因素。ESMM乘法形式对应的损失函数如下：
$$L({\theta }_{cvr},{\theta }_{ctr})=\sum _{i=1}^{N}l(y_i,f(x_i;{\theta }_{ctr}))+\sum _{i=1}^{N}l(y_i\&z_i,f(x_i;{\theta }_{ctr})\ast f(x_i;{\theta }_{cvr}))$$
${\theta }_{cvr},{\theta }_{ctr}$ :CVR 与 CTR网络的参数；l()：交叉熵损失函数

• 共享特征表示
  如图2中所示，embedding层把大规模稀疏输入数据映射到低纬的表示向量，占据了整个网络参数的绝大部分，需要大量的训练样本才能充分学习得到。在ESMM模型中，CTR的训练样本量远远大于CVR的训练样本量，这种共享特征表示也可以让CVR从只有展现没有点击的样本进行学习，从而缓解数据稀疏性的问题。

实验

• 数据集

由于ESMM创造性的利用了用户行为序列作为模型的训练样本，因此没有公开的数据集，所以从淘宝的日志中采样了一部分数据，作为公开的数据集，其下载地址为：https://tianchi.aliyun.com/dataset/dataDetail?dataId=408&userId=1

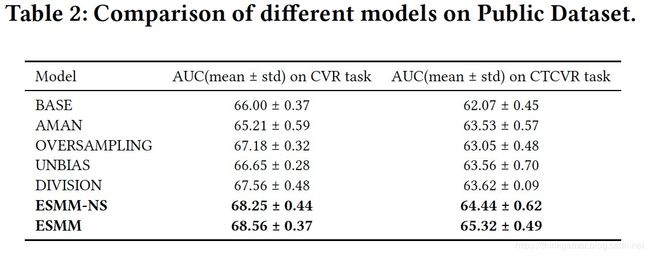
• 对比测试

为了保证实验的有效性，在以下四方面是相同的。

1.使用ReLU激活函数

2.embedding向量的纬度是18

3.MLP的层数是：360 * 200 * 80 * 2

4.adam的参数是：beta1 = 0.9 beta2 = 0.999 e=10^-8

Adam算法介绍：https://www.jianshu.com/p/aebcaf8af76e

几种常见的优化算法对比：https://zhuanlan.zhihu.com/p/22252270

---

打开微信扫一扫，关注微信公众号【搜索与推荐Wiki】