深入理解单模匹配算法之KMP

单模匹配算法KMP

问题的提出

有两个字符串S1和S2，问S1是否是S2的子串。
这样的问题我们称为模式匹配问题。在这里我们称S1为模式串，S2为主串。
所谓单模匹配，指模式串只有一个，对主串的数量则没有要求。
举个单模匹配的例子：
模式串为：“apple”
主串有三个，分别为
主串1 “i like apple”,
主串2 “apple is fruit”
主串3 “banana is also fruit”
问：“apple”是否是这些主串的子串？
答案显而易见，主串1和主串2中含有单词“apple”，而主串3中则没有。
需要注意的是单模匹配有的时候不光考虑主串是否包含模式串，还考虑模式串在主串中的位置（即模式串的第一个字母在主串中的位置）。在下标从1开始的情况下
对于主串1，“apple”在其中的位置为8
对于主串2，“apple”在其中的位置为1

利用暴力法来解决这个问题

暴力法是可以用来解决这个问题的。用一个例子来说明暴力法的过程。
模式串为abd
主串为cabcabda
首先比较主串的第1个字母c和模式串的第1个字母a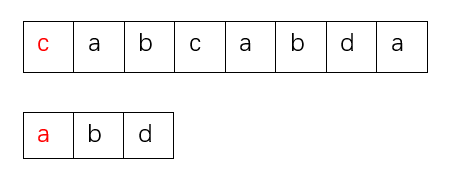
发现二者不相同，那么模式串整体后移一位，之后比较主串的第2个字母a和模式串的第1个字母a

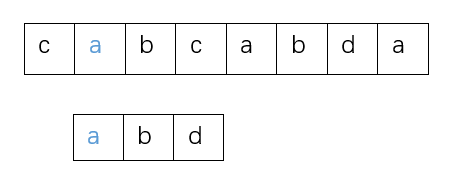
发现二者相同，之后比较主串的第3个字母b和模式串的第2个字母b

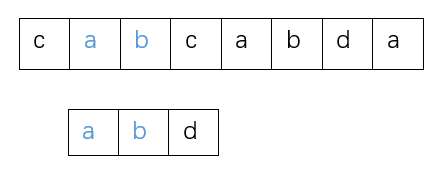
发现二者相同，之后比较主串的第4个字母c和模式串的第3个字母d

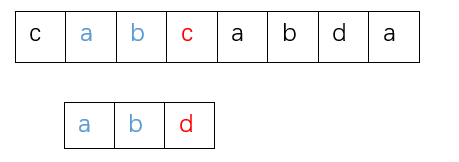
发现二者不相同，那么模式串整体后移一位，之后比较主串的第3个字母b和模式串的第1个字母a

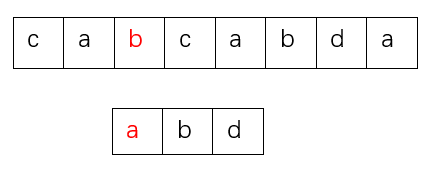
发现二者不相同，那么模式串整体后移一位，之后比较主串的第4个字母c和模式串的第1个字母a

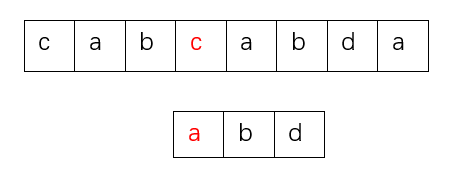
发现二者不相同，那么模式串整体后移一位，之后比较主串的第5个字母a和模式串的第1个字母a

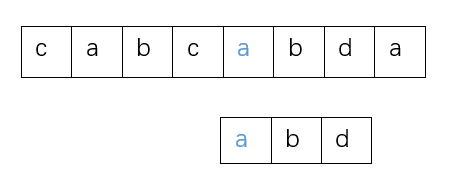
发现二者相同，之后比较主串的第6个字母b和模式串的第2个字母b

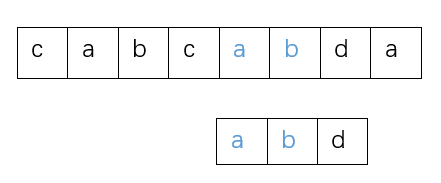
发现二者相同，之后比较主串的第7个字母d和模式串的第3个字母d

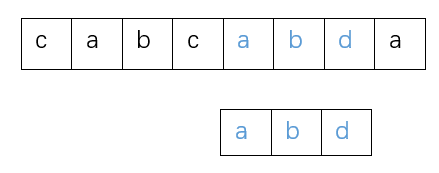
于是在主串中找到了模式串，模式串在主串中的位置是5
下面给出暴力法的代码实现。

int violence(string mainStr, string subStr)//输入主串和模式串，输出模式串在主串的位置，没有则返回-1
{
	for (int i = 0; i < mainStr.size(); i++)//遍历主串
	{
		for (int j = 0; j < subStr.size(); j++)
		{
			if (i + j >= mainStr.size())//模式串的最后一个字母位置不可超出主串
				break;
			if (mainStr[i + j] != subStr[j])//比较主串和模式串的第j个字母
			{
				break;//不相同则退出此次循环
			}
			if (j == subStr.size() - 1)//若果模式串全部遍历完还没退出，说明在主串中找到了模式串（因为模式串有一个字母和主串不匹配都会退出）
				return i;//返回模式串在主串的位置
		}
	}
	return -1;//没找到，返回-1
}

暴力法的缺点

暴力法的思路简单直接，但是时间复杂度较高，为O(n²)。经分析，匹配失败后模式串每次都只向右移动1位，我们可不可以让模式串不是移动1位而是多移动几位呢？这样不就比暴力法更快一些吗？
于是出现了KMP算法，它可以让模式串不是一个格子一个格子“挪动”，而是在有必要的时刻“跳”一个大步子，加速匹配过程。

KMP算法

KMP算法中最关键的概念叫做next数组，next数组的作用就是：决定模式串在匹配失败后需要移动的步长。需要注意的是next数组属于模式串而不是主串。

如何获得next数组?

首先给出几个概念

前缀：空字符串或包含字符串第一个字符的任意连续的子串（不包含自身）。
如对于 apple 这个字符串， 空字符串，a，ap，app，appl 都是前缀。

后缀：空字符串或包含字符串最后一个字符的任意连续的子串（不包含自身）。
如对于 apple 这个字符串， 空字符串，e，le，ple，pple 都是后缀。

公共前后缀：对于某一个字符串，它的前缀和后缀中如果存在相同的，那么该字符串就是公共前后缀。
例如对于 abcab 这个字符串
它的前缀有 空字符串，a，ab，abc，abca
它的后缀有 空字符串，b，ab，cab，bcab
前缀和后缀中相同的有 空字符串，ab
那么公共前后缀就是 空字符串 和 ab

最大公共前后缀：对于某一个字符串，公共前后缀中长度最长的那个就是最大公共前后缀。
例如对于 abcab 这个字符串
它的前缀有 空字符串，a，ab，abc，abca
它的后缀有 空字符串，b，ab，cab，bcab
公共前后缀有 空字符串，ab
最长的是 ab
于是最大公共前后缀是ab

最大公共前后缀的数字表示法：
最大公共前后缀可以用一个数字来表示。这个数字是：最大公共前后缀的长度。
为什么呢？我们来看一下如何用最大公共前后缀的数字表示法来获得最大公共前后缀。只要通过数字表示法可以获得最大公共前后缀，我们就可以这样表示。
对于 abcab 这个字符串，在上文已经知道最大公共前后缀的长度是2，则数字表示法为2
那么我们可以从第一个字符开始，依次取2个字符得到 ab
这个就是最大公共前后缀。
需要注意的是空字符串的最大公共前后缀的数字表示法定义为-1.

(最大公共前后缀的)数字表示法的递推公式
正因为数字表示法可以用递推公式来计算，才出现了KMP算法。
这里的递推公式表示：对于某个字符串S1，我如果已知其数字表示法，那么当在S后新加一个字符后，我可以用递推公式计算新字符串S2 的数字表示法。
说人话就是，我知道 S1 = abcab 的数字表示法，当我再加一个新字符 c 构成 S2 = abcabc 时，可以通过S1的数字表示法简单计算获得S2的数字表示法。
接下来用例子来理解一下递推公式。
已知字符串 abcab 的数字表示法为2，根据新增加的字符不同讨论递推公式的形式。

第一种情况：

新增加的字符与 原字符串 数字表示法的数字对应的下标处 所对应的字符相同
上面这句话有点绕口，用例子来看一下
下面是原始字符串S1，蓝色的部分是最大公共前后缀，数字表示法为2，则 数字表示法对应的下标处 的字符为c 。（默认下标是从0开始的）

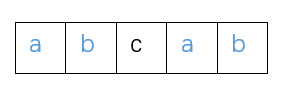
当新增加的字符为c时，即满足上述条件。

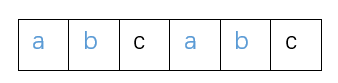
比 较新增字符 和 数字表示法对应的下标处的 c

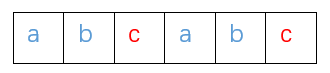
发现二者相同，那么新字符串abcabc的数字表示法为原字符串abcab的数字表示法加1

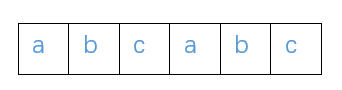
第二种情况：

新增加的字符与 原字符串 数字表示法的数字对应的下标处 所对应的字符不相同
原始字符串为abcab

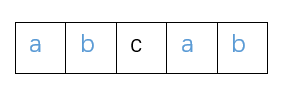
除了c以外，随便选一个新增字符，这里就以a为例

发现c和a不相同，我们需要做的事情是把原字符串的最大公共前后缀拿出来

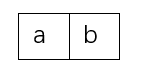
之后在原字符串最大公共前后缀后加上新字符

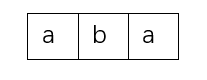
之后计算上述字符串的最大公共前后缀。按照此方法计算出的最大公共前后缀就是新字符串abcaba的最大公共前后缀。
这里是KMP最难理解的地方。下面的文字请多读几遍，看懂了也就搞定了KMP。
在新增字符a为不相同的情况下，计算abcaba的最大公共前后缀本质就是计算原字符前缀ab的所有前缀和后缀aba的所有后缀中相同而且最大的字符串，是两个字符串之间计算最大公共前后缀，和之前给出的单字符串的最大公共前后缀的定义不太一样了。其他的教程并没有指出这点，所以很难理解。但是前缀ab又一定是后缀aba的前缀，因为原来的前后缀是一样的都是ab，我们只是在后缀上加了一个字符a，前缀没有变，那么新的前缀一定是新的后缀的前缀。那么在前后缀两个字符串之间计算最大公共前后缀的问题就可以转化为求新后缀的最大公共前后缀。

最大公共前后缀和next数组的关系

其实next数组就是最大公共前后缀的数组。next数组的下标n不为0时，存的值就是 模式串 下标0到n-1的子串 的 最大公共前后缀数字表示法，也就是原数组所有前缀的数字表示法。next数组的下标n为0时存的是-1 ，这么取纯粹是为了递推过程方便，也就是为了推导出空字符串的数字表示法为0（上面定义里有，忘记了可以返回去看看）。
例如 abcab 的next数组可这样来生成。
首先对于下标0，空字符串的数字表示法为-1。其实定义为-1纯粹是为了写代码方便。

之后对于下标1，计算a的最大前后缀。这里的计算方式和上面给出的递推算法不太一样，为：上一步的数字表示法为-1就加1。这里属于特殊的边界数值计算方法，不需要太纠结，只需要知道怎么算即可。这么做的好处是可以套到之前的递推公式中。

之后对于下标2，计算ab的最大前后缀。新增的字符b和a的数字表示法0对应的字符a不一样，则按照上述迭代公式，计算a的最大公共前后缀空字符串，加上新字符b生成的新字符串b的最大公共前后缀。新字符串b会进入上一步next[1]的特殊的边界数值计算，结果为0。所以ab的最大公共前后缀为0 。

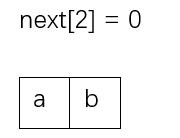
之后对于下标3，计算abc的最大前后缀。方法和上一步差不多。新增的字符c和a的数字表示法0对应的字符a不一样，则按照上述迭代公式，计算a的最大公共前后缀空字符串，加上新字符c生成的新字符串c的最大公共前后缀。
新字符串b会进入上一步next[1]的特殊的边界数值计算，结果为0。所以abc的最大公共前后缀为0 。

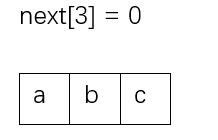
之后对于下标4，计算abca的最大前后缀。发现新增a和和a的数字表示法0对应的字符a一样，新的数字表示法为0+1=1 。

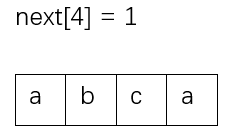
到此全过程结束。代码如下所示。

void calNextVector(string str, int* next)//计算next数组
{
	int k = -1;//k代表当前字符串新加字符时，当前字符串的数字表示法，初始为-1即next[0]=-1
	int j = 0;//j代表前缀的长度，从空字符开始递推
	next[0] = k;//next[0]=-1
	while (j < str.size() - 1)//递推过程
	{
		if (k == -1 || str[k] == str[j])//k == -1代表特殊边界条件，str[k] == str[j]表示新增字符和数字表示法处的字符相同
		{
			k++;//数字表示法加1
			j++;//下标加1
			next[j] = k;
		}
		else//此处代表str[k] ！= str[j]，新增字符和数字表示法处的字符不相同
		{
			k = next[k];//去找最大公共前后缀加上新字符后的最大公共前后缀，该过程等价于把当前的数字表示法改变为最大公共前后缀的数字表示法
		}
	}
}

使用next数组进行模式匹配

next数组是为了加快模式匹配的速度，那这个过程是怎么实现的？
考虑如下的情况，模式串在第4个字符处匹配失败了

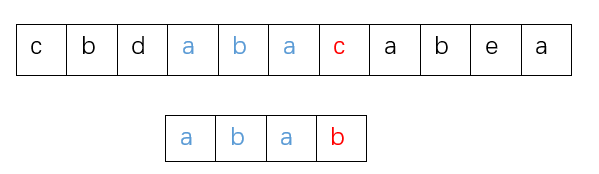
这时候观察模式串失配字符前的子串aba，在图中用绿色标出它的最大公共前后缀

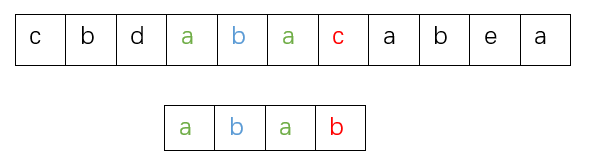
我们直接让模式串移动 失配位置（从0开始算，b位置是3） - 当前前缀的最大公共前后缀长度（1）= 2 个格子即可。

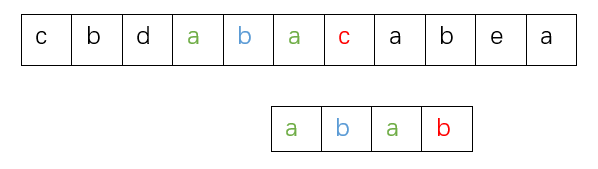
为什么这样做？经观察，这里的字符串匹配可以拆分为先做模式串中的aba的前缀和主串中aba后缀的匹配，再考虑后面其他部分的匹配。所以只需要把主串中aba的后缀和模式串中aba的前缀对齐即可。在不丢失信息的情况下一定是按照最大公共前后缀来匹配，因为如果不按照最大公共前后缀来匹配，也就是按照更短的前后缀来匹配，那一定是丢丢失了最大公共前后缀匹配的信息；如果按照最大前后缀来匹配则不会丢失更短的前后缀的匹配信息。
所以移动的本质就是让aba中前缀(a)ba移动到后缀ab(a)处，使括号中的两个最大前后缀重合。移动的长度就是ab的长度，即aba的长度减去aba最大公共前后缀的长度。而aba的长度又与失配处的下标值相同，所以最公式终变为：失配位置 - 当前前缀的最大公共前后缀长度。
移动后可以忽略 模式串前缀aba 的前缀（这一段已经匹配过了，不需要重复匹配），直接从b开始继续和主串匹配。所以此时，已经匹配的长度变为前缀aba的最大公共前后缀长度。
下面给出匹配部分的代码。

int KMP(string mainStr, string subStr, int* next)
{
	int i = 0;//遍历主串
	int j = 0;//当前已匹配部分的数字表示法
	while (i < mainStr.size())
	{
		cout << i << endl;
		while (subStr[j] == mainStr[i + j])//如匹配成功
		{
			if (j < subStr.size() - 1)
			{
				j++;//匹配成功,继续匹配下一个字符
			}
			else if (j == subStr.size() - 1)//j == subStr.size() - 1代表模式串全部匹配成功
			{
				return i;//返回模式串在主串的位置
			}
		}
		i += (j - next[j]);//失配，利用next数组计算主串指针的跳转步长
		if (j != 0)
		{
			j = next[j];//失配，若已匹配部分不为空，更新已匹配部分为当前已匹配部分的最大公共前后缀，用数字表示法存储
		}
	}
	return -1;//没在主串中找到模式串返回-1
}

完整代码

#include 
#include 
using namespace std;

void calNextVector(string str, int* next)
{
	int k = -1;//k代表当前字符串新加字符时，当前字符串的数字表示法，初始为-1即next[0]=-1
	int j = 0;//j代表前缀的长度，从空字符开始递推
	next[0] = k;//next[0]=-1
	while (j < str.size() - 1)//递推过程
	{
		if (k == -1 || str[k] == str[j])//k == -1代表特殊边界条件，str[k] == str[j]为新增字符和数字表示法处的字符相同
		{
			k++;
			j++;
			next[j] = k;
		}
		else//此处代表str[k] ！= str[j]，新增字符和数字表示法处的字符不相同
		{
			k = next[k];//去找最大公共前后缀加上新字符后的最大公共前后缀，该过程等价于把当前的数字表示法改变为最大公共前后缀的数字表示法
		}
	}
}

int KMP(string mainStr, string subStr, int* next)
{
	int i = 0;//遍历主串
	int j = 0;//当前已匹配部分的数字表示法
	while (i < mainStr.size())
	{
		cout << i << endl;
		while (subStr[j] == mainStr[i + j])//如匹配成功
		{
			if (j < subStr.size() - 1)
			{
				j++;//匹配成功,继续匹配下一个字符
			}
			else if (j == subStr.size() - 1)//j == subStr.size() - 1代表模式串全部匹配成功
			{
				return i;//返回模式串在主串的位置
			}
		}
		i += (j - next[j]);//失配，利用next数组计算主串指针的跳转步长
		if (j != 0)
		{
			j = next[j];//失配，若已匹配部分不为空，更新已匹配部分为当前已匹配部分的最大公共前后缀，用数字表示法存储
		}
	}
	return -1;//没在主串中找到模式串返回-1
}

int main()
{
	string subStr;//模式串
	cin >> subStr;//输入模式串
	int* next = new int[subStr.size()];
	calNextVector(subStr, next);//计算next数组
	string mainStr;//主串
	while (cin >> mainStr)//循环输入主串
	{
		int ans = KMP(mainStr, subStr, next);
	
		if (ans == -1)//没找到
		{
			cout << "No substring!" << endl;
		}
		else//找到了，打印位置
		{
			cout << "Find substring at " << ans << ".（Index start with 0.）" << endl;//
		}
	}
	delete[] next;
	return 0;
}