中文词性标注详解

所谓的词性标注在NLP领域是一个应用非常广泛的技术，总的来说，词性标注所解决的问题就是说，给定一句话 $s$，我们将$s$进行分词操作，可以将 $s$ 分成 $n$ 个词，那么 $s$ 可以表示成：$s=w_1{w}_2...w_n$，我们将这 $n$ 个词每一个词标注一个词性那么这句话词性可以表示成 $t=z_1{z}_2...z_n$。在这个前提下，我们给定一句新的话术 $s^{\prime }={w_1}^{\prime }{w_2}^{\prime }...{w_n}^{\prime }$，如何自动给这句话的每个词打上标签呢？也就是求出 $t^{\prime }={z_1}^{\prime }{z_2}^{\prime }...{z_n}^{\prime }$，这就是词性标注的作用。如图所示就是词性标注的示意图：

这个问题可以用概率的知识来解释，我们可以把词性标注的问题建立一个概率的模型。在给定一个句子的前提下，求序列标注的概率我们可以表示成 $p(t|s)$，我们需要做的就是将这个概率最大化，在 $p(t|s)$ 取得最大值的时候，所得到的标注序列 $t$，就是我们要得到的结果，接下来我们就要最大化这个概率。
好了，我们来看 $p(t|s)$ 这个概率表达式，运用贝叶斯定理，我们可以得到如下的等式： $p(t|s)=p(s|t)p(t)$，那么我们可以将 $p(t|s)$ 拆成两项相乘的形式，前面一项是一个 translation model，后面一项是 language model。我们继续将这个表达式进行展开，可以得到：
$$p(t|s)=p(s|t)p(t)=p(w_1{w}_2...w_n|z_1{z}_2...z_n)p(z_1{z}_2...z_n)$$
接下来，我们可以将上述表达式进行展开操作，因为：
$$p(w_1{w}_2...w_n|z_1{z}_2...z_n)p(z_1{z}_2...z_n)=p(w_1{w}_2...w_n\cdot z_1{z}_2...z_n)$$
然后我们可以继续将表达式进行分解：
$$p(w_1{w}_2...w_n\cdot z_1{z}_2...z_n)=p(w_1|w_2...w_n{z}_1{z}_2...z_n)p(w_2...w_n{z}_1{z}_2...z_n)$$
由马尔科夫假设我们可以得到：
$$p(w_1|w_2...w_n{z}_1{z}_2...z_n)=p(w_1|z_1)$$
那么可以得到：
$$p(w_1{w}_2...w_n\cdot z_1{z}_2...z_n)=p(w_1|z_1)p(w_2...w_n{z}_1{z}_2...z_n)$$
同理以此类推，我们可以得到一个最终的表达式：
$$p(w_1{w}_2...w_n\cdot z_1{z}_2...z_n)=\prod _{i=1}^{n}p(w_i|z_i)\cdot p(z_1)p(z_2|z_1)p(z_3|z_2)...p(z_n|z_{n-1})$$
在这个表达式中我们可以清楚地看到一些特性，$\prod _{i=1}^{n}p(w_i|z_i)$ 就表示发射概率，后面的 $p(z_2|z_1)p(z_3|z_2)...p(z_n|z_{n-1})$ 表示状态转移概率，$p(z_1)$ 表示初始的状态概率。我们最后需要最大化这三项表达式的乘积。用表达式可以写成：
$$\hat{z}=\arg \max p(z|s)=\arg \max \prod _{i=1}^{n}p(w_i|z_i)\prod _{j=2}^{n}p(z_j|z_{j-1})p(z_1)$$
为了方便求解，我们将表达式进行求对数操作：
$$\hat{z}=\arg \max \log [\prod _{i=1}^{n}p(w_i|z_i)\prod _{j=2}^{n}p(z_j|z_{j-1})p(z_1)]$$
然后我们可以将乘积的形式变成求和的形式，也就是最终我们求解的目标函数：
$$\hat{z}=\underset{z}{\mathrm{argmax}}[\sum _{i=1}^n\log p(w_i|z_i)+\log p(z_i)+\sum _{j=2}^n\log p(z_j|z_{j-1})]$$
在我之前的博客 隐马尔科夫模型(HMM)算法的理解与超详细推导 中有详细介绍过HMM，这里我们用 $A$ 表示发射概率，也就是 $p(w_i|z_i)$，$B$ 表示状态转移概率 $p(z_i|z_{i-1})$，然后 $\pi$ 表示初始状态 $p(z_1)$。
好了，理清了整个中文词性标注的逻辑之后，我们首先要求 $A、B、\pi$，然后根据维特比算法求得 $z$ 序列的最大值，将我们z 的序列解码出来，这就是整个词性标注的流程和逻辑。首先我们来看一下训练的数据，我是在网上下载的人民日报词性标注的训练集，这个训练集网上很多地方可以下载到，然后都是从人民日报中的摘要进行词性标注出来的，内容如图所示：

里面已经分好词并且标注好词性了，每一句话就是一行，总共是两万多条。接下来我们来看发射概率矩阵 $A$：

再来看看状态转移概率矩阵 $B$:

好了，有了$A$ 和 $B$，我们暂时把初始概率矩阵 $\pi$ 先不管，我们来建立词典和标签映射，代码如下：

tag2id, id2tag = {}, {}
word2id, id2word = {}, {}

for line in open('dataset/pos_tag_dataset.txt', encoding='utf-8'):
    if line:
        for items in line.split('  '):
            item = items.split('/')
            if len(item)==2:
                word, tag = item[0], item[1].rstrip()

                if word not in word2id:
                    word2id[word] = len(word2id)
                    id2word[len(id2word)] = word
                if tag not in tag2id:
                    tag2id[tag] = len(tag2id)
                    id2tag[len(id2tag)] = tag

M = len(word2id)
N = len(tag2id)

这里 $M$ 表示词典的大小，也就是词的数量。$N$ 表示词性的数量，我们整个词库有55317个词和45中词性，如图所示：

然后我们可以开始构建 $A、B、\pi$，代码如下所示：

# 构建 pi A B
import numpy as np
pi = np.zeros(N)
A = np.zeros((N, M))
B = np.zeros((N, N))

接下来，我们需要为 $A、B、\pi$ 填值了，首先我们需要统计发射矩阵出现的次数和转移矩阵出现的次数以及初始状态的次数，
我们只需要解析 tag 的前后关系和 tag 与 word 的关系，代码如下所示：

for line in open('dataset/pos_tag_dataset.txt',encoding='utf-8'):
    if line:
        prev_tag = ''
        for items in line.split('  '):
            item = items.split('/')
            if len(item)==2:
                wordId, tagId = word2id[item[0]], tag2id[item[1].rstrip()]
                if prev_tag == '': # 句子的开始
                    pi[tagId] += 1
                    A[tagId][wordId] += 1
                else:
                    A[tagId][wordId] += 1
                    B[tag2id[prev_tag]][tagId] += 1

                if item[0] == '。':
                    prev_tag = ''
                else:
                    prev_tag = item[1]

这样的代码很简洁，也很容易理解，我们统计好词频之后，再将我们的 $A、B、\pi$ 进行归一化，就是我们的发射概率矩阵，状态转移概率矩阵和初始矩阵了，代码如下所示：

# normalize
pi = pi / sum(pi)
for i in range(N):
    A[i] /= sum(A[i])
    B[i] /= sum(B[i])

然后我们可以看看 $A、B、\pi$ 的结果如下：



然后我们可以定义一个 log 函数，当我们概率为零的时候，需要加入一个平滑：

def log(x):
    if x == 0:
        return np.log(0.00001)
    else:
        return np.log(x)

接下来我们就要开始用维特比算法进行解码操作，所谓的维特比算法，就是运用我们动态规划的算法思想。整体的流程如下所示：

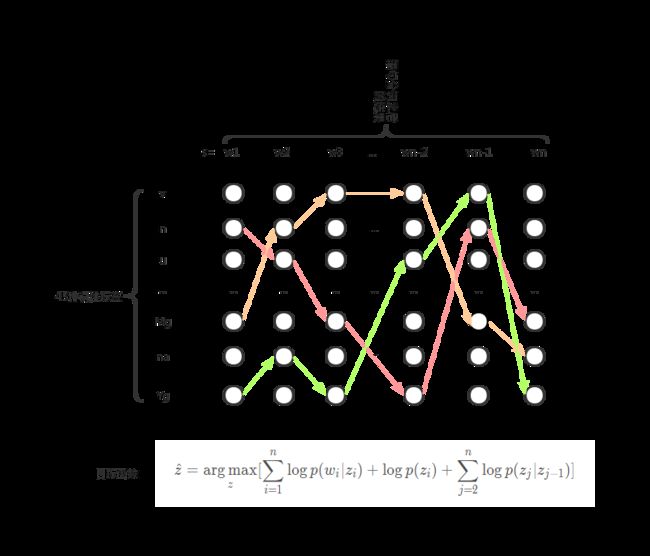
在图中横坐标是我们分词之后的词，纵坐标是我们的45个不同的词性，我们需要的就是找到一条路径从第一个词到最后一个词，使得路径所对应的目标函数最大，我们就取这条路径所对应的词性序列作为最后这个话术的词性标注。在图中，我们可以看到红色、橘黄色和绿色的线都可以成为序列标注的路径。那么我们总共可以有 $N=45^n$ 种路径，如果我们要把 $45^n$ 种路径全部遍历一遍，那将是灾难级别的时间复杂度，所以这里我们使用维特比算法，运用动态规划的思想来解决这个问题。
我们每向前走一步，就记录当前的最佳的路径，直到最后。走完最后一个词之后，我们可以取出整个流程的最佳路径，这就是维特比算法的大体流程，代码如下所示：

def viterbi(x, pi, A, B):
    '''
    x: 输入的句子
    pi:初始状态
    A:发射概率
    B:转移概率
    '''
    seg_list = jieba.cut(x)
    x = [word2id[word] for word in seg_list]
    T = len(x)
    
    dp = np.zeros((T,N)) # dp[i][j]:w1,w2,...,wT, 假设wi的tag是第j个tag
    # basecase for dp algorithm
    pointer = np.array([[0 for x in range(N)] for y in range(T)]) # T*N
    
    for j in range(N):
        dp[0][j] = log(pi[j]) + log(A[j][x[0]])
    for i in range(1, T): # 词语
        for j in range(N): # 词性
            dp[i][j] = float("-inf")
            for k in range(N): # 从每一个k词性到j
                score = dp[i-1][k] + log(B[k][j]) + log(A[j][x[i]])
                if score > dp[i][j]:
                    dp[i][j] = score
                    pointer[i][j] = k
    # decoding: 把最好的tag seq打印出来
    best_seq = [0 for _ in range(T)]
    # step1： 找出对应于最后一个单词的词性
    best_seq[T-1] = np.argmax(dp[T-1])
    # step2: 通过从后到前的循环依次求出每个单词的词性
    for i in range(T-2, -1, -1):
        best_seq[i] = pointer[i+1][best_seq[i+1]]
    # 到目前为止 best_seq存放了对应于x的词性序列
    for i in range(len(best_seq)):
        print(id2tag[best_seq[i]])

最后我们就可以打印出，每句话的最佳序列标注，我们来测试一个：

这个序列和我们训练数据中的进行对比：

结果上来看基本上没有问题，但是要注意的是：这里用的是 jieba 分词，很多分词之后的结果和我们训练数据中的结果不一样，所以很多情况下在词典中找不到 jieba 分词之后的词的 id，所以我们再标注训练数据的时候尽量应该和我们分词的结果一致，这样就不会有问题了。
这就是从最底层实现了整个中文词性标注的流程，希望在词性标注方面对大家有所帮助，详细代码可以参考 GitHub ，谢谢。