【 FPGA/IC 】常考加法器总结

早在某发科提前批中就考到过加法器，如果没有记错的话，当时的加法器是串行加法器。

今天就谈谈这几种加法器。

1、等波纹进位加法器（Ripple carry adder circuit）

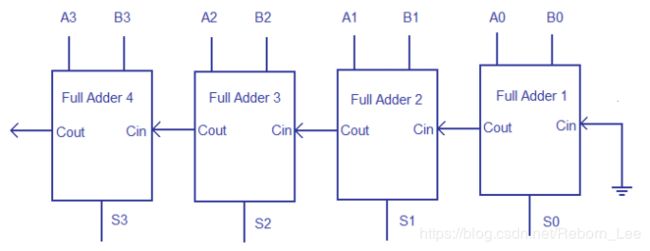
如下图为一个4位的等波纹进位加法器：

它是由4个1位的全加器构成，每一级的全加器的进位作为下一级的进位。

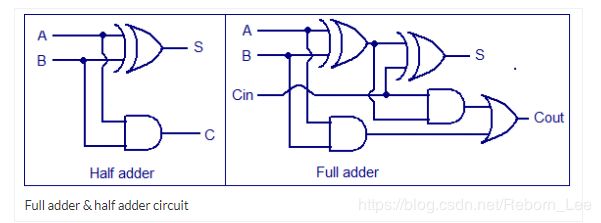
1位全加器是由组合逻辑构成的，如下图：

可知，全加器的表达式：

Si=Ai⊕Bi⊕Ci-1

或者

可想而知，随着加法器位数的增加，每一级的延迟会逐渐积累，导致总的延迟过大。

参考链接

---

2、进位选择加法器（carry select adder）

下面给出一种貌似更优化点的加法器，这种加法器虽然浪费了一点资源，但是体现了用面积换速度的思想（逻辑复制），那就是进位选择加法器：

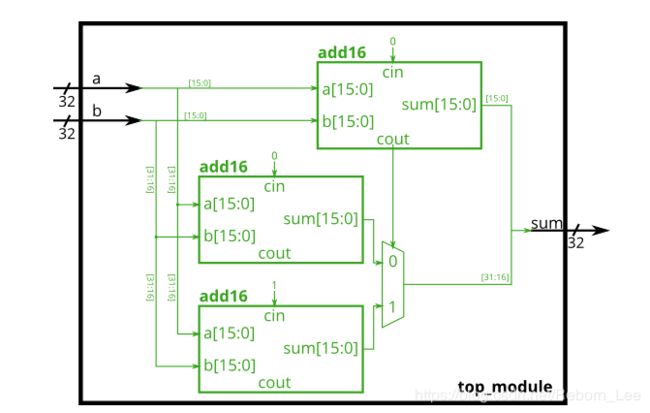
具体说来，假如一个32位的加法器，如果采用等波纹进位加法器，设计思想就是前16级加法器的进位输出作为后16级加法器的进位输入，这样计算出32位相加的结果需要耗费两个16位数据相加的加法器时间；但如果如下设计：

也就是后16位数据的相加复制两份，不同的仅仅是进位不同，由前16位数据相加的进位来选择，所用的时间就会相对于等波纹进位加法器减少了一半。

module top_module(
    input [31:0] a,
    input [31:0] b,
    output [31:0] sum
);
    wire [15:0] sum1,sum2,sum3;
    wire cout1;
    add16 inst1_add16(
        .a(a[15:0]),
        .b(b[15:0]),
        .cin(1'b0),
        .sum(sum1),
        .cout(cout1)
    );
    
    add16 inst2_add16(
        .a(a[31:16]),
        .b(b[31:16]),
        .cin(1'b0),
        .sum(sum2),
        .cout()
    );
    add16 inst3_add16(
        .a(a[31:16]),
        .b(b[31:16]),
        .cin(1'b1),
        .sum(sum3),
        .cout()
    );
    
    wire [15:0] sum4;
    assign sum4 = cout1 ? sum3 : sum2; 
    
    assign sum = {sum4, sum1};

endmodule

16位的加法器请自行描述。

参考链接

---

3、串行加法器

这个加法器就有名堂了，它只用一个全加器资源，就可以完成任意个位数的加法。

它需要和时钟同步，有多少位就需要多少个时钟，对速度要求不是太高的设计还是可以考虑的。

在串行加法器中，只有一个全加器，数据逐位串行送入加法器进行运算，如图所示。图中FA是全加器，A、B是两个具有右移功能的寄存器，C为进位触发器。由移位寄存器从低位到高位逐位串行提供操作数相加。如果操作数长n位，加法就要分n次进行，每次产生一位和，并串行地送回A寄存器。进位触发器用来寄存进位信号，以便参与下一次的运算。
 

下面给出其真值表（假设是8位相加）（这个真值表就是考试内容呀）：

串行加法器

A	B	Cin	S	Cout
1	0	0	1	0
0	1	0	1	0
1	1	0	0	1
0	0	1	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
1	1	0	0	1

参考链接

4、超前进位加法器(Carry-Lookahead Adder，CLA)

超前进位加法器是相对于等波纹进位加法器而言的，而RCA（等波纹进位加法器）的效率太低，高位的输出必须等到低位算完才行。

解决的办法就是CLA：

那4位加法器为例：

如下是等波纹加法器的展开图：

 

其中一个全加器的参数来表示后面的进位输出（Cout），即：

由此来表示4个全加器的进位输出为：

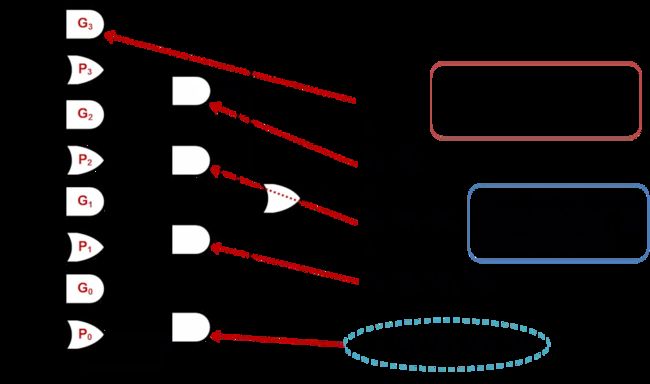
最终我们需要得到的是C4，经过换算，C4=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0+P3·P2·P1·P0·C0，而这些参数，全部已知！并不需要前一个全加器运算输出，由此我们得到了提前计算进位输出的方法， 用这样的方法实现了加法器就被称为超前进位加法器（Carry-Lookahead Adder，CLA）。

根据上面的优化算法，我们重新绘制了CLA的布线方式：

显而易见，与等波纹加法器相比，逻辑延迟小多了。

尽管优点很明显，但是实现却很复杂，这是缺点，对于更高位的加法，我们通常用多个小规模的CLA拼接成一个较大的加法器，例如：

用4个8-bit的超前进位加法器连接成32-bit加法器。

参考链接