Tensorflow 实现多项式回归之二 (附完整实现代码)

多项式回归

之前写过一篇基于BP神经网络并且利用扩张特征的方法来实现多项式回归的方法。这里使用另一种方式来完成回归。

方法概述

这里使用另一种方式来完成多项式回归。之前的方法是使用了简单的神经网络，且网络结构比较简单（没有隐藏层），方法不灵活。这里使用的方式是通过添加隐藏层以及使用sigmoid函数来引入非线性特性，从而达到非线性回归的目的。话不多说，直接上代码。。

---

引入必要的包

import tensorflow as tf
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt

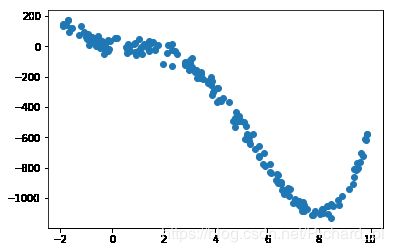
创建数据这里的目的函数为 $y=x^4-12x^3+16x^2-10x+4$，并引入噪声（高斯分布）。

def f(x):
    return x**4 - 12 * x**3 + 16*x**2 - 10* x + 4
data_size = 200
mean = 0
stddev = 30
noise = np.random.normal(mean, stddev, data_size)
x = np.random.uniform(low = -2, high = 10, size = data_size)
y = np.array(list(map(f, x)) + noise)

plt.figure()
plt.scatter(x, y)
plt.show()

关键代码

创建四层网络，第一层为输入层，第二层100个节点，第三层40个节点，第四层一个节点（两个隐藏层）

sess = tf.InteractiveSession()

w1 = tf.Variable(tf.truncated_normal([1, 100], stddev = 0.1))
b1 = tf.Variable(tf.constant(0.1, shape = [100]))

w2 = tf.Variable(tf.zeros([100, 40]))
b2 = tf.Variable(tf.zeros([40]))

w3 = tf.Variable(tf.zeros([40, 1]))
b3 = tf.Variable(tf.zeros([1]))

input_x = tf.placeholder(tf.float32, [None, 1])
y_ = tf.placeholder(tf.float32, [None, 1])

使用概率选择节点，避免过拟合现象。使用sigmoid函数来引入非线性特性 & 使用自使用优化函数 AdamOptimizer

hiddern = tf.nn.sigmoid(tf.matmul(input_x, w1) +b1)

keep_prob = tf.placeholder(tf.float32)
h_drop = tf.nn.dropout(hiddern, keep_prob)

hiddern2 = tf.nn.sigmoid(tf.matmul(h_drop, w2) + b2)

y_pred = tf.matmul(hiddern2, w3) + b3
# y_pred = tf.matmul(hiddern2, w3) + b3


loss = tf.reduce_mean(tf.square(y_-y_pred))
train_step = tf.train.AdamOptimizer(0.002).minimize(loss)

训练模型，每隔1000次打印loss

tf.global_variables_initializer().run()
batch_size = 50
for i in range(20000):
    rand_index = np.random.choice(data_size, size=batch_size)
    batch_xs = np.mat(x[rand_index]).transpose()
    batch_ys = np.mat(y[rand_index]).transpose()
    if i % 1000 == 0:
        train_loss = loss.eval(feed_dict = {input_x:batch_xs, y_:batch_ys, keep_prob:1.0})
        print('step {}, training loss is {}'.format(i, train_loss))
        if train_loss < 5000:
            break
    train_step.run(feed_dict = {input_x: batch_xs, y_:batch_ys, keep_prob:0.75})

step 0, training loss is 282864.3125
step 1000, training loss is 272062.46875
step 2000, training loss is 270302.5625
step 3000, training loss is 136706.921875
step 4000, training loss is 155461.84375
step 5000, training loss is 172553.0
step 6000, training loss is 60845.9765625
step 7000, training loss is 83346.6015625
step 8000, training loss is 38959.19921875
step 9000, training loss is 39800.171875
step 10000, training loss is 34262.5234375
step 11000, training loss is 26534.7890625
step 12000, training loss is 11538.2587890625
step 13000, training loss is 9259.6416015625
step 14000, training loss is 10335.1953125
step 15000, training loss is 6591.216796875
step 16000, training loss is 9328.1552734375
step 17000, training loss is 9821.3369140625
step 18000, training loss is 3219.609130859375

定义测试代码

test = np.mat([i for i in range(0, 11, 1)]).transpose()
predict = y_pred.eval(feed_dict = {input_x: test, keep_prob: 1.0})

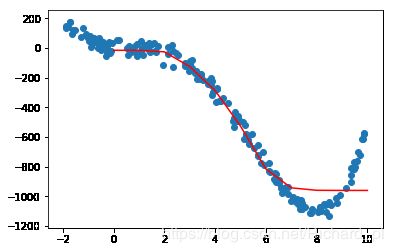
测试并图形化展示

test = list(np.array(test).reshape(-1, 1))
predict = list(predict)
plt.figure()
plt.plot(test, predict, c = 'r')
plt.scatter(x, y)
plt.show()