信号峰拟合的MATLAB程序，包括高斯拟合，多高斯拟合等多种类型

今天准备弄双高斯拟合，看到一个信号峰拟合的MATLAB版本的程序，大体看了一下，很不错，先MARK一下，以后再详细研究。

 http://terpconnect.umd.edu/~toh/spectrum/CurveFittingC.html

http://terpconnect.umd.edu/~toh/spectrum/InteractivePeakFitter.htm  

下面是其CODE。感叹别人的代码写的那个结构可扩展性，牛人啊！先来看他的一个双高斯拟合示例：


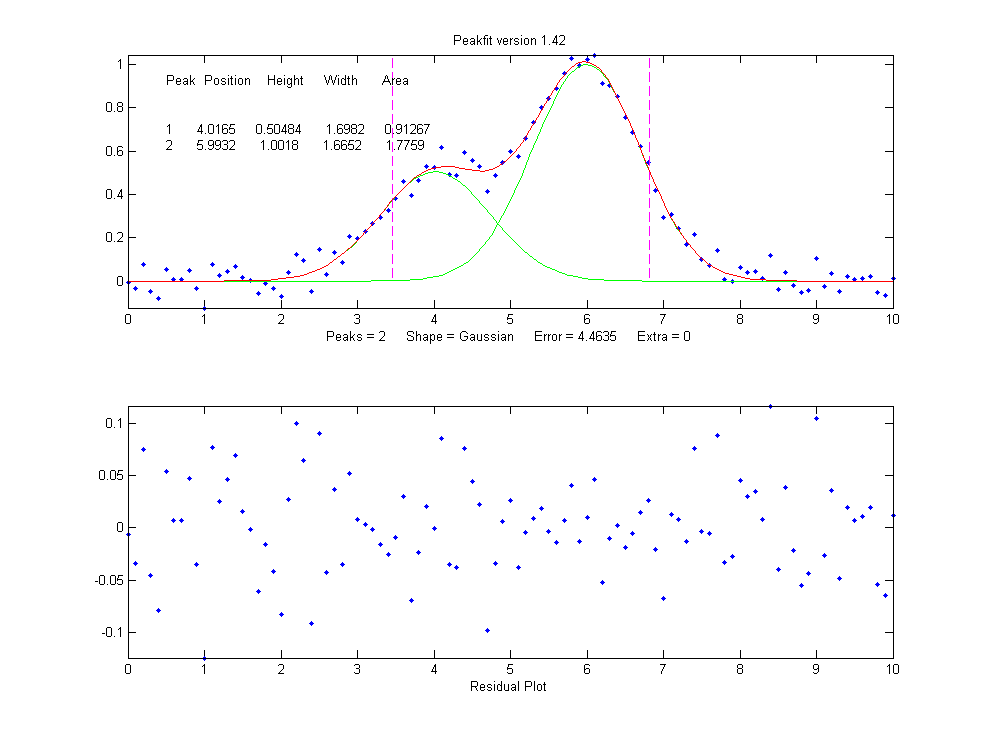
下面是MATLAB峰拟合函数：

function [FitResults,LowestError,BestStart,xi,yi]=peakfit(signal,center,window,NumPeaks,peakshape,extra,NumTrials,start,AUTOZERO)
% Version 2.2: October, 2011. Adds exponential pulse and sigmoid models
% A command-line peak fitting program for time-series signals, 
% written as a self-contained Matlab function in a single m-file. 
% Uses an non-linear optimization algorithm to decompose a complex, 
% overlapping-peak signal into its component parts. The objective
% is to determine whether your signal can be represented as the sum of
% fundamental underlying peaks shapes. Accepts signals of any length,
% including those with non-integer and non-uniform x-values. Fits 
% Gaussian, equal-width Gaussians, exponentially-broadened Gaussian, 
% Lorentzian, equal-width Lorentzians, Pearson, Logistic, exponential
% pulse, abd sigmoid shapes (expandable to other shapes). This is a command
% line version, usable from a remote terminal. It is capable of making 
% multiple trial fits with sightly different starting values and taking
% the one with the lowest mean fit error.  Version 2.2: Sept, 2011.
%
% PEAKFIT(signal);       
% Performs an iterative least-squares fit of a single Gaussian  
% peak to the data matrix "signal", which has x values 
% in column 1 and Y values in column 2 (e.g. [x y])
%
% PEAKFIT(signal,center,window);
% Fits a single Gaussian peak to a portion of the 
% matrix "signal". The portion is centered on the 
% x-value "center" and has width "window" (in x units).
% 
% PEAKFIT(signal,center,window,NumPeaks);
% "NumPeaks" = number of peaks in the model (default is 1 if not
% specified). 
% 
% PEAKFIT(signal,center,window,NumPeaks,peakshape);
% Specifies the peak shape of the model: "peakshape" = 1-5.
% (1=Gaussian (default), 2=Lorentzian, 3=logistic, 4=Pearson, 
% 5=exponentionally broadened Gaussian; 6=equal-width Gaussians;
% 7=Equal-width Lorentzians; 8=exponentionally broadened equal-width
% Gaussian, 9=exponential pulse, 10=sigmoid).
%
% PEAKFIT(signal,center,window,NumPeaks,peakshape,extra)
% Specifies the value of 'extra', used in the Pearson and the
% exponentionally broadened Gaussian shapes to fine-tune the peak shape. 
% 
% PEAKFIT(signal,center,window,NumPeaks,peakshape,extra,NumTrials);
% Performs "NumTrials" trial fits and selects the best one (with lowest
% fitting error). NumTrials can be any positive integer (default is 1).
%
% PEAKFIT(signal,center,window,NumPeaks,peakshape,extra,NumTrials,start)
% Specifies the first guesses vector "firstguess" for the peak positions
%  and widths, e.g. start=[position1 width1 position2 width2 ...]
% 
% [FitResults,MeanFitError]=PEAKFIT(signal,center,window...)
% Returns the FitResults vector in the order peak number, peak
% position, peak height, peak width, and peak area), and the MeanFitError
% (the percent RMS difference between the data and the model in the
% selected segment of that data) of the best fit.
%
% Optional output parameters 
% 1. FitResults: a table of model peak parameters, one row for each peak,
%    listing Peak number, Peak position, Height, Width, and Peak area.
% 2. LowestError: The rms fitting error of the best trial fit.
% 3. BestStart: the starting guesses that gave the best fit.
% 4. xi: vector containing 100 interploated x-values for the model peaks. 
% 5. yi: matrix containing the y values of each model peak at each xi. 
%    Type plot(xi,yi(1,:)) to plot peak 1 or plot(xi,yi) to plot all peaks
%
% T. C. O'Haver ([email protected]). Version 2.2 
%  
% Example 1: 
% >> x=[0:.1:10]';y=exp(-(x-5).^2);peakfit([x y])
% Fits exp(-x)^2 with a single Gaussian peak model.
%
%        Peak number  Peak position   Height     Width      Peak area
%             1            5            1        1.665       1.7725
%
% Example 2:
% x=[0:.1:10]';y=exp(-(x-5).^2)+.1*randn(size(x));peakfit([x y])
% Like Example 1, except that random noise is added to the y data.
% ans =
%             1         5.0279       0.9272      1.7948      1.7716
%
% Example 3:
% x=[0:.1:10];y=exp(-(x-5).^2)+.5*exp(-(x-3).^2)+.1*randn(size(x));
% peakfit([x' y'],5,19,2,1,0,1)
% Fits a noisy two-peak signal with a double Gaussian model (NumPeaks=2).
% ans =
%             1       3.0001      0.49489        1.642      0.86504
%             2       4.9927       1.0016       1.6597       1.7696
%
% Example 4:
% >> y=lorentzian(1:100,50,2);peakfit(y,50,100,1,2)
% Create and fit Lorentzian located at x=50, height=1, width=2.
% ans =
%            1           50      0.99974       1.9971       3.1079
% Example 5: 
%   >> x=[0:.005:1];y=humps(x);peakfit([x' y'],.3,.7,1,4,3);
%   Fits a portion of the humps function, 0.7 units wide and centered on 
%   x=0.3, with a single (NumPeaks=1) Pearson function (peakshape=4)
%   with extra=3 (controls shape of Pearson function).
%
% Example 6: 
%  >> x=[0:.005:1];y=(humps(x)+humps(x-.13)).^3;smatrix=[x' y'];
%  >> [FitResults,MeanFitError]=peakfit(smatrix,.4,.7,2,1,0,10)
%  Creates a data matrix 'smatrix', fits a portion to a two-peak Gaussian
%  model, takes the best of 10 trials.  Returns FitResults and MeanFitError.
%  FitResults =
%              1      0.31056  2.0125e+006      0.11057  2.3689e+005
%              2      0.41529  2.2403e+006      0.12033  2.8696e+005
%  MeanFitError =
%         1.1899
%
% Example 7:
% >> peakfit([x' y'],.4,.7,2,1,0,10,[.3 .1 .5 .1]);
% As above, but specifies the first-guess position and width of the two
% peaks, in the order [position1 width1 position2 width2]
%
% Example 8:
% >> peakfit([x' y'],.4,.7,2,1,0,10,[.3 .1 .5 .1],0);
% As above, but sets AUTOZERO mode in the last argument.
% AUROZERO=0 does not subtract baseline from data segment. 
% AUROZERO=1 (default) subtracts linear baseline from data segment.
% AUROZERO=2, subtracts quadratic baseline from data segment.
%
% For more details, see
% http://terpconnect.umd.edu/~toh/spectrum/CurveFittingC.html and
% http://terpconnect.umd.edu/~toh/spectrum/InteractivePeakFitter.htm
%
global AA xxx PEAKHEIGHTS

format short g
format compact
warning off all

datasize=size(signal);
if datasize(1)X(length(X)),
    disp('X-axis flipped.')
    X=fliplr(X);
    Y=fliplr(Y);
end
% Y=Y-min(Y);  % Remove excess offset from data
% Isolate desired segment from data set for curve fitting
if nargin==1 || nargin==2,center=(max(X)-min(X))/2;window=max(X)-min(X);end
xoffset=center-window/2;
n1=val2ind(X,center-window/2);
n2=val2ind(X,center+window/2);
if window==0,n1=1;n2=length(X);end
xx=X(n1:n2)-xoffset;
yy=Y(n1:n2);
ShapeString='Gaussian';

% Define values of any missing arguments
switch nargin
    case 1
        NumPeaks=1;
        peakshape=1;
        extra=0;
        NumTrials=1;
        xx=X;yy=Y;
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 2
        NumPeaks=1;
        peakshape=1;
        extra=0;
        NumTrials=1;
        xx=signal;yy=center;
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 3
        NumPeaks=1;
        peakshape=1;
        extra=0;
        NumTrials=1;
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 4
        peakshape=1;
        extra=0;
        NumTrials=1;
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 5
        extra=0;
        NumTrials=1;
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 6
        NumTrials=1;
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 7
        start=calcstart(xx,NumPeaks,xoffset);
        AUTOZERO=1;
    case 8
        AUTOZERO=1;
    otherwise
end % switch nargin

% Remove baseline from data segment (alternative code)
% lxx=length(xx);
% bkgsize=10;
% if AUTOZERO==1,  % linear autozero operation  
%     XX1=xx(1:round(lxx/bkgsize));
%     XX2=xx((lxx-round(lxx/bkgsize)):lxx);
%     Y1=yy(1:round(length(xx)/bkgsize));
%     Y2=yy((lxx-round(lxx/bkgsize)):lxx);
%     bkgcoef=polyfit([XX1,XX2],[Y1,Y2],1);  % Fit straight line to sub-group of points
%     bkg=polyval(bkgcoef,xx);
%     yy=yy-bkg;
% end % if

% Remove baseline from data segment
X1=min(xx);X2=max(xx);Y1=min(Y);Y2=max(Y);
if AUTOZERO==1, % linear autozero operation  
  Y1=mean(yy(1:length(xx)/20));
  Y2=mean(yy((length(xx)-length(xx)/20):length(xx)));
  yy=yy-((Y2-Y1)/(X2-X1)*(xx-X1)+Y1);
end % if

if AUTOZERO==2, % Quadratic autozero operation  
    XX1=xx(1:round(lxx/bkgsize));
    XX2=xx((lxx-round(lxx/bkgsize)):lxx);
    Y1=yy(1:round(length(xx)/bkgsize));
    Y2=yy((lxx-round(lxx/bkgsize)):lxx);
    bkgcoef=polyfit([XX1,XX2],[Y1,Y2],2);  % Fit parabola to sub-group of points
    bkg=polyval(bkgcoef,xx);
    yy=yy-bkg;
end % if autozero

PEAKHEIGHTS=zeros(1,NumPeaks);
n=length(xx);
newstart=start;
switch NumPeaks
    case 1
        newstart(1)=start(1)-xoffset;
    case 2
        newstart(1)=start(1)-xoffset;
        newstart(3)=start(3)-xoffset;
    case 3
        newstart(1)=start(1)-xoffset;
        newstart(3)=start(3)-xoffset;
        newstart(5)=start(5)-xoffset;
    case 4
        newstart(1)=start(1)-xoffset;
        newstart(3)=start(3)-xoffset;
        newstart(5)=start(5)-xoffset;
        newstart(7)=start(7)-xoffset;
     case 5
        newstart(1)=start(1)-xoffset;
        newstart(3)=start(3)-xoffset;
        newstart(5)=start(5)-xoffset;
        newstart(7)=start(7)-xoffset;        
        newstart(9)=start(9)-xoffset;
     case 6
        newstart(1)=start(1)-xoffset;
        newstart(3)=start(3)-xoffset;
        newstart(5)=start(5)-xoffset;
        newstart(7)=start(7)-xoffset;        
        newstart(9)=start(9)-xoffset;
        newstart(11)=start(11)-xoffset;
    otherwise       
end % switch NumPeaks

% Perform peak fitting for selected peak shape using fminsearch function
options = optimset('TolX',.00001,'Display','off' );
LowestError=1000; % or any big number greater than largest error expected
FitParameters=zeros(1,NumPeaks.*2); 
BestStart=zeros(1,NumPeaks.*2); 
height=zeros(1,NumPeaks); 
bestmodel=zeros(size(yy));
for k=1:NumTrials, 
    % disp(['Trial number ' num2str(k) ] ) % optionally prints the current trial number as progress indicator
  switch peakshape
    case 1
        TrialParameters=fminsearch(@fitgaussian,newstart,options,xx,yy);
        ShapeString='Gaussian';
    case 2
        TrialParameters=fminsearch(@fitlorentzian,newstart,options,xx,yy);
        ShapeString='Lorentzian';    
    case 3
        TrialParameters=fminsearch(@fitlogistic,newstart,options,xx,yy);
        ShapeString='Logistic';
    case 4
        TrialParameters=fminsearch(@fitpearson,newstart,options,xx,yy,extra);
        ShapeString='Pearson';
    case 5
        TrialParameters=fminsearch(@fitexpgaussian,newstart,options,xx,yy,-extra);
        ShapeString='ExpGaussian';
    case 6
        cwnewstart(1)=newstart(1);
        for pc=2:NumPeaks,
            cwnewstart(pc)=newstart(2.*pc-1);  
        end
        cwnewstart(NumPeaks+1)=(max(xx)-min(xx))/5;
        TrialParameters=fminsearch(@fitewgaussian,cwnewstart,options,xx,yy);
        ShapeString='Equal width Gaussians';
    case 7
        cwnewstart(1)=newstart(1);
        for pc=2:NumPeaks,
            cwnewstart(pc)=newstart(2.*pc-1);  
        end
        cwnewstart(NumPeaks+1)=(max(xx)-min(xx))/5;
        TrialParameters=fminsearch(@fitlorentziancw,cwnewstart,options,xx,yy);
        ShapeString='Equal width Lorentzians';
    case 8
        cwnewstart(1)=newstart(1);
        for pc=2:NumPeaks,
            cwnewstart(pc)=newstart(2.*pc-1);  
        end
        cwnewstart(NumPeaks+1)=(max(xx)-min(xx))/5;
        TrialParameters=fminsearch(@fitexpewgaussian,cwnewstart,options,xx,yy,-extra);
        ShapeString='Exp. equal width Gaussians';
    case 9
        TrialParameters=fminsearch(@fitexppulse,newstart,options,xx,yy);
        ShapeString='Exponential Pulse';   
    case 10
        TrialParameters=fminsearch(@fitsigmoid,newstart,options,xx,yy);
        ShapeString='Sigmoid';       
      otherwise
  end % switch peakshape
  
% Construct model from Trial parameters
A=zeros(NumPeaks,n);
for m=1:NumPeaks,
   switch peakshape
    case 1
        A(m,:)=gaussian(xx,TrialParameters(2*m-1),TrialParameters(2*m));
    case 2
        A(m,:)=lorentzian(xx,TrialParameters(2*m-1),TrialParameters(2*m));
    case 3
        A(m,:)=logistic(xx,TrialParameters(2*m-1),TrialParameters(2*m));
    case 4
        A(m,:)=pearson(xx,TrialParameters(2*m-1),TrialParameters(2*m),extra);
    case 5
        A(m,:)=expgaussian(xx,TrialParameters(2*m-1),TrialParameters(2*m),-extra)';
    case 6
        A(m,:)=gaussian(xx,TrialParameters(m),TrialParameters(NumPeaks+1));
    case 7
        A(m,:)=lorentzian(xx,TrialParameters(m),TrialParameters(NumPeaks+1));  
    case 8
        A(m,:)=expgaussian(xx,TrialParameters(m),TrialParameters(NumPeaks+1),-extra)';    
    case 9
        A(m,:)=exppulse(xx,TrialParameters(2*m-1),TrialParameters(2*m));  
    case 10
        A(m,:)=sigmoid(xx,TrialParameters(2*m-1),TrialParameters(2*m)); 
       otherwise
  end % switch
      switch NumPeaks % adds random variation to non-linear parameters
       case 1
          newstart=[newstart(1)*(1+randn/50) newstart(2)*(1+randn/10)]; 
       case 2
          newstart=[newstart(1)*(1+randn/50) newstart(2)*(1+randn/10) newstart(3)*(1+randn/50) newstart(4)*(1+randn/10)]; 
       case 3
          newstart=[newstart(1)*(1+randn/50) newstart(2)*(1+randn/10) newstart(3)*(1+randn/50) newstart(4)*(1+randn/10) newstart(5)*(1+randn/50) newstart(6)*(1+randn/10)]; 
       case 4
          newstart=[newstart(1)*(1+randn/50) newstart(2)*(1+randn/10) newstart(3)*(1+randn/50) newstart(4)*(1+randn/10) newstart(5)*(1+randn/50) newstart(6)*(1+randn/10)  newstart(7)*(1+randn/50) newstart(8)*(1+randn/10)]; 
       case 5
          newstart=[newstart(1)*(1+randn/50) newstart(2)*(1+randn/10) newstart(3)*(1+randn/50) newstart(4)*(1+randn/10) newstart(5)*(1+randn/50) newstart(6)*(1+randn/10)  newstart(7)*(1+randn/50) newstart(8)*(1+randn/10)  newstart(9)*(1+randn/50) newstart(10)*(1+randn/10)]; 
       otherwise       
     end % switch NumPeaks
end % for
% Multiplies each row by the corresponding amplitude and adds them up
model=PEAKHEIGHTS'*A;

% Compare trial model to data segment and compute the fit error
  MeanFitError=100*norm(yy-model)./(sqrt(n)*max(yy));
  % Take only the single fit that has the lowest MeanFitError
  if MeanFitError0,  % Consider only fits with positive peak heights
        LowestError=MeanFitError;  % Assign LowestError to the lowest MeanFitError
        FitParameters=TrialParameters;  % Assign FitParameters to the fit with the lowest MeanFitError
        BestStart=newstart; % Assign BestStart to the start with the lowest MeanFitError
        height=PEAKHEIGHTS; % Assign height to the PEAKHEIGHTS with the lowest MeanFitError
        bestmodel=model; % Assign bestmodel to the model with the lowest MeanFitError
      end % if min(PEAKHEIGHTS)>0
  end % if MeanFitError0];
g = p';
% ----------------------------------------------------------------------
function err = fitsigmoid(tau,x,y)
% Fitting function for iterative fit to the sum of
% sigmiods of the form Height./(1 + exp((t1 - t)/t2))
global PEAKHEIGHTS
A = zeros(length(x),round(length(tau)/2));
for j = 1:length(tau)/2,
    A(:,j) = sigmoid(x,tau(2*j-1),tau(2*j));
end
PEAKHEIGHTS = A\y';
z = A*PEAKHEIGHTS;
err = norm(z-y');
% ----------------------------------------------------------------------
function g=sigmoid(x,t1,t2)
g=1./(1 + exp((t1 - x)./t2))';