机器学习算法原理总结系列---算法基础之(6)支持向量机(Support Vectors Machine)

一、原理详解

1. 背景：
   1.1 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出
   1.2 目前的版本(soft margin)是由Corinna Cortes 和 Vapnik在1993年提出，并在1995年发表
   1.3 深度学习（2012）出现之前，SVM被认为机器学习中近十几年来最成功，表现最好的算法

2. 机器学习的一般框架：
   训练集 => 提取特征向量 => 结合一定的算法（分类器：比如决策树，KNN）=>得到结果

3. 介绍：
   3.1 例子：
   
   思考一下，两类？哪条线最好？

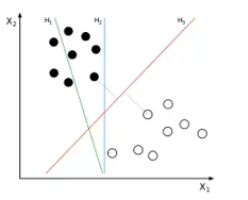
   3.2 SVM寻找区分两类的超平面（hyper plane), 使边际(margin)最大
   
   总共可以有多少个可能的超平面？无数条
   如何选取使边际(margin)最大的超平面 (Max Margin Hyperplane)？
   超平面到一侧最近点的距离等于到另一侧最近点的距离，两侧的两个超平面平行

现在对于SVM算法有了基本初步的认识。先介绍两个概念，以方便更加深入研究SVM。

4.线性可区分(linear separable) 和 线性不可区分 （linear inseparable)


这三种都是线性不可分的。最开始介绍的例子是线性可分的。

好，知道这样的概念后，之后咱们先深入讨论线性可区分的情况。

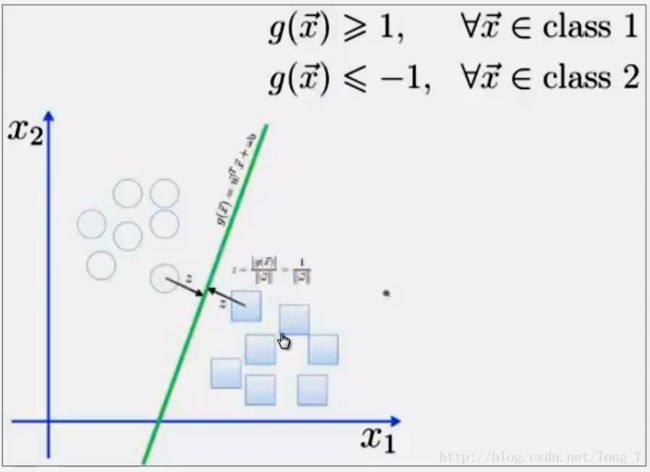
5 . 线性可区分情况的SVM定义与公式建立

超平面可以定义为：
W: weight vector, , n 是特征值的个数
X: 训练实例
b: bias

5.1 假设2维特征向量：X = (x1, X2) （如3.2的两个图所示）
把 b 想象为额外的 weight
超平面方程变为：

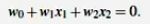
所有超平面右上方的点满足：

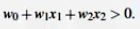
所有超平面左下方的点满足：

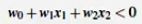
调整weight，使超平面定义边际的两边：

综合以上两式，得到： (1)

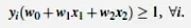
所有坐落在边际的两边的的超平面上的被称作“支持向量(support vectors)”
分界的超平面和H1或H2上任意一点的距离为： (i.e.: 其中||W||是向量的范数(norm))

所以，最大边际距离为：

6 . 求解

6.1 SVM如何找出最大边际的超平面呢(MMH)？

利用一些数学推倒，以上公式 （1）可变为有限制的凸优化问题(convex quadratic optimization)
利用 Karush-Kuhn-Tucker (KKT)条件和拉格朗日公式，可以推出MMH可以被表示为以下“决定边界 (decision boundary)”:

其中，

6.2 对于任何测试（要归类的）实例，带入以上公式，得出的符号是正还是负决定

SVM深层的数学原理是很复杂的，所以咱们可以慢慢研究，一点点吃透。

7 . 例子：

所以SVM算法特性：

• 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以SVM不太容易产生overfitting
• SVM训练出来的模型完全依赖于支持向量(Support Vectors), 即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。
• 一个SVM如果训练得出的支持向量个数比较小，SVM训练出的模型比较容易被泛化。

8 . 线性不可区分的情况

8.1 数据集在空间中对应的向量不可被一个超平面区分开

8.2 两个步骤来解决：

• 8.2.1 利用一个非线性的映射把原数据集中的向量点转化到一个更高维度的空间中
• 8.2.2 在这个高维度的空间中找一个线性的超平面来根据线性可分的情况处理
  
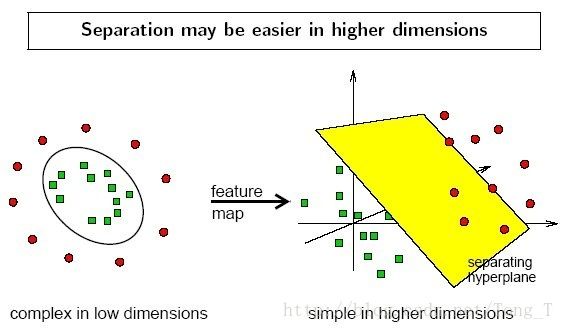
  另外一个例子：
  
• 8.2.3 视觉化演示 https://r2—sn-oguesnze.googlevideo.com/videoplayback?dur=0.000&source=youtube&ratebypass=yes&lmt=1298954202315842&key=cms1&expire=1514442365&clen=1590919&pl=20&mime=video%2Fwebm&itag=43&ei=HTpEWp_LMMi1qQGl9bSACQ&sparams=clen,dur,ei,expire,gir,id,initcwndbps,ip,ipbits,itag,lmt,mime,mm,mn,ms,mv,pl,ratebypass,requiressl,source&ipbits=0&id=o-AIN1PtbEQ_Ht_dHdXsA7ZdA1okvZJ84f9pf60MqQoPQp&requiressl=yes&ip=175.201.48.185&signature=0D1C738A0755FE5D5F162B457438B40E932AC56B.23B38DA65C2D2AE43B51FA7889F64AB3AC679EF5&gir=yes&redirect_counter=1&cm2rm=sn-3u-3fwz7k&req_id=80e896301ba4a3ee&cms_redirect=yes&mm=29&mn=sn-oguesnze&ms=rdu&mt=1514420682&mv=m

8.3 如何利用非线性映射把原始数据转化到高维中？

9 . 核方法（kernel trick)

同样的结果，使用kernel方法计算容易很多

二、代码示例：

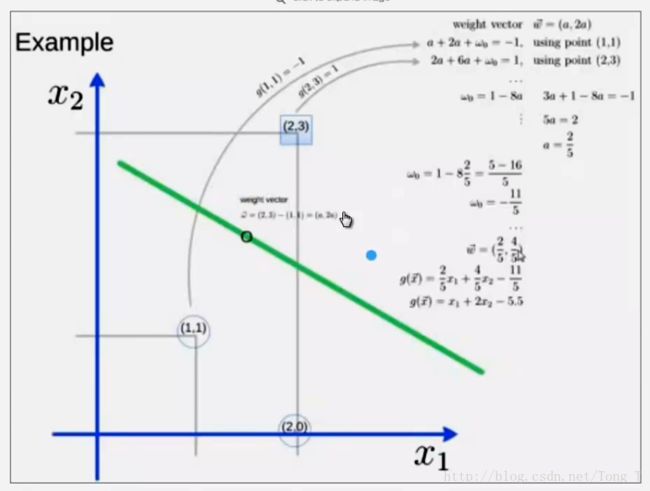
任务1：用代码实现7例子中的example：

from sklearn import svm

X = [[2, 0], [1, 1], [2, 3]]
y = [0, 0, 1]
clf = svm.SVC(kernel='linear')
clf.fit(X, y)

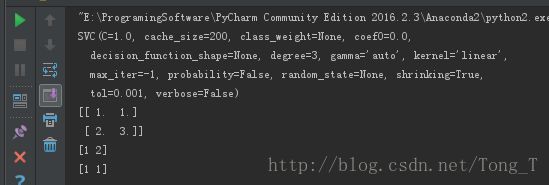
print(clf)

# get support vectors
print(clf.support_vectors_)

# get indices of support vectors
print(clf.support_)

# get number of support vectors for each class
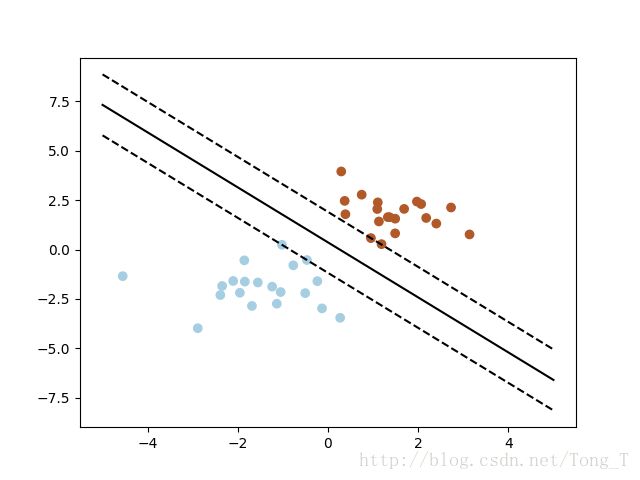
print(clf.n_support_)

任务2：随机生成分类点，画出svm分类图

print(__doc__)

import numpy as np
import pylab as pl
from sklearn import svm

# we create 40 separable points
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
Y = [0] * 20 + [1] * 20

# fit the model
clf = svm.SVC(kernel='linear')
clf.fit(X, Y)

# get the separating hyperplane
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (clf.intercept_[0]) / w[1]

# plot the parallels to the separating hyperplane that pass through the
# support vectors
b = clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])

print("w: ", w)
print("a: ", a)
# print " xx: ", xx
# print " yy: ", yy
print("support_vectors_: ", clf.support_vectors_)
print("clf.coef_: ", clf.coef_)

# In scikit-learn coef_ attribute holds the vectors of the separating hyperplanes for linear models. It has shape (n_classes, n_features) if n_classes > 1 (multi-class one-vs-all) and (1, n_features) for binary classification.
# In this toy binary classification example, n_features == 2, hence w = coef_[0] is the vector orthogonal to the hyperplane (the hyperplane is fully defined by it + the intercept).
# To plot this hyperplane in the 2D case (any hyperplane of a 2D plane is a 1D line), we want to find a f as in y = f(x) = a.x + b. In this case a is the slope of the line and can be computed by a = -w[0] / w[1].
# plot the line, the points, and the nearest vectors to the plane
pl.plot(xx, yy, 'k-')
pl.plot(xx, yy_down, 'k--')
pl.plot(xx, yy_up, 'k--')

pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
           s=80, facecolors='none')
pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired)

pl.axis('tight')
pl.show()