【数据结构】算法2.22-2.23 一元多项式的表示及相加

#include
#include
#include

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2

typedef int Status;
typedef struct
{
    int coef;   //系数
    int expn;   //指数
}term,ElemType;
typedef struct LNode
{
    ElemType data;
    struct LNode *next;
}LNode,*Link,*Position;
typedef struct
{
    Link head,tail;
    int len;
}LinkList;
typedef LinkList polynomial;

/*******************************声明部分****************************************/
Status MakeNode (Link *p,ElemType *e);
//分配由p指向的值为e的结点，并返回OK，
void FreeNode(Link p);
//释放p所指结点
Status InitList(LinkList *L);
//构造一个空的线性链表L
Status InsFirst(LinkList *L,Link h,Link *s);
//已知h指向线性链表的头结点，将s所指结点插入在第一个结点之前
Status DelFirst(LinkList *L,Link h,Link *q);
//已知h指向线性链表的头结点，删除链表中第一个结点并以q返回
Status Append(LinkList *L,Link *s);
//将指针s所指（彼此以指针相连）的一串结点链接在线性链表L的最后一个结点
//之后，并改变链表L的尾指针指向新的尾结点
Status SetCurElem(Link p,ElemType e);
//已知p指向线性链表中的一个结点，用e更新p所指结点中数据元素的值
ElemType GetCurElem(Link p);
//已知p指向线性链表中的一个结点，返回p所指结点中数据元素的值
Position GetHead(LinkList L);
//返回线性链表L中头结点的位置
Position NextPos(LinkList L,Link p);
//已知p指向线性链表L中的一个结点，返回p所指结点的直接后继的位置
//Position LocateElem(LinkList L,ElemType e,Status(*compare)(ElemType,ElemType));
//返回线性链表L中第一个与e满足函数compare（）判定关系的元素的位置
Status LocateElem(LinkList L,ElemType e,Position *q,int (*cmp)(ElemType,ElemType));
//若有序链表L中存在与e满足判定函数cmp取值为0的元素，则q指示L中第一个值为e的结点的位置
//并返回TRUE，否则q指示第一个与e满足判定函数cmp取值>0的元素的前驱位置，并返回FALSE
int cmp(term a,term b);
//依a的指数值>或=或1,0，+1
void CreatePolyn(polynomial *P,int m);
//输入m项的系数和指数，建立表示一元多项式的有序链表P
/*******************************函数部分****************************************/
Status MakeNode (Link *p,ElemType *e)
{

    *p = (Link)malloc(sizeof(LNode));
    if(!*p)
        exit(OVERFLOW);
    (*p)->data = *e;
    (*p)->next = NULL;
    return OK;
}

void FreeNode(Link p)
{
    p = NULL;
    free(p);
}

Status InitList(LinkList *L)
{
    Link p;  //head node;
    p = (Link)malloc(sizeof(LNode));
    if(!p)
        exit(OVERFLOW);
    L->head = L->tail = p;
    L->len = 0;
    p->next = NULL;
    return OK;
}

Status InsFirst(LinkList *L,Link h,Link *s)
{
    (*s)->next = h->next;
    h->next = *s;
    L->len++;
    if(h == L->tail)
        L->tail = h->next;
    return OK;
}

Status DelFirst(LinkList *L,Link h,Link *q)
{
    Link p;

    *q = h->next;
    h->next = (*q)->next;
    if(!h->next)
        (*L).tail = h;
    L->len--;
    return OK;
}

Status Append(LinkList *L,Link *s)
{
    int i = 0;
    (*L).tail->next = *s;
    while(*s){
        *s = (*s)->next;
        i++;
    }
    (*L).tail = *s;
    (*L).len += i;
}

Status SetCurElem(Link p,ElemType e)
{
    p->data = e;
    return OK;
}

ElemType GetCurElem(Link p)
{
    return p->data;
}

Position GetHead(LinkList L)
{
    return L.head;
}

Position NextPos(LinkList L,Link p)
{
    return p->next;
}

/*
Position LocateElem(LinkList L,ElemType e,Status(*compare)(ElemType,ElemType))
{
    Position p;
    p = L.head;
    while(p->next){
        if(compare(p->data,e))
            return p;
        p = p->next;
    }
    return ERROR;
}*/

Status ListEmpty(LinkList L)
{
    return (L.len == 0);
}

int cmp(term a,term b)
{

    if(a.expn > b.expn)
        return 1;
    else if(a.expn == b.expn)
        return 0;
    else
        return -1;
}

Status LocateElem(LinkList L,ElemType e,Position *q,int (*cmp)(ElemType,ElemType))
{
    Link p,pre;
    p = L.head;
    do{
        pre = p;
        p = p->next;
    }while(p!=NULL && cmp(p->data,e)<0);
    if(p==NULL || cmp(p->data,e)>0){
        *q = pre;
        return FALSE;
    }
    else{
        *q = p;
        return TRUE;
    }
}

void CreatePolyn_1(polynomial *P,int m)
{
    Link h,q,s;
    term e;
    int i;

    InitList(P);
    h = GetHead(*P);
    e.coef = 0.0;
    e.expn = -1;
    SetCurElem(h,e);

    int coef_list[4] = {7,3,9,5};
    int expn_list[4] = {0,1,8,17};

    for(i = 0;i<m;++i){
      /*  printf("输入第%d个非零项的系数：",i);
        scanf("%d",&e.coef);
        printf("输入第%d个非零项的指数：",i);
        scanf("%d",&e.expn);*/
        e.coef = coef_list[i];
        e.expn = expn_list[i];

        if(!LocateElem(*P,e,&q,cmp)){
            if(MakeNode(&s,&e))
                InsFirst(P,q,&s);
        }//if
    }//for
}

void CreatePolyn_2(polynomial *P,int m)
{
    Link h,q,s;
    term e;
    int i;

    InitList(P);
    h = GetHead(*P);
    e.coef = 0.0;
    e.expn = -1;
    SetCurElem(h,e);

    int coef_list[3] = {8,22,-9};
    int expn_list[3] = {1,7,8};

    for(i = 0;i<m;++i){
        e.coef = coef_list[i];
        e.expn = expn_list[i];

        if(!LocateElem(*P,e,&q,cmp)){
            if(MakeNode(&s,&e))
                InsFirst(P,q,&s);
        }//if
    }//for
}

void AddPolyn(polynomial *Pa,polynomial *Pb)
{
    Link ha,hb,qa,qb;
    term a,b;
    int sum;

    ha = GetHead(*Pa);
    hb = GetHead(*Pb);
    qa = NextPos(*Pa,ha);
    qb = NextPos(*Pb,hb);

    while(qa && qb){
        a = GetCurElem(qa);
        b = GetCurElem(qb);

        switch(cmp(a,b))
        {
        case -1:
            ha = qa;
            qa = NextPos(*Pa,qa);
            break;
        case 0:
            sum = a.coef+b.coef;
            if(sum != 0.0){
                qa->data.coef = sum;
                SetCurElem(qa,qa->data);
                ha = qa;
            }//if
            else{
                DelFirst(Pa,ha,&qa);
                FreeNode(qa);
            }
            DelFirst(Pb,hb,&qb);
            FreeNode(qb);
            qb = NextPos(*Pb,hb);
            qa = NextPos(*Pa,ha);
            break;
        case 1:
            DelFirst(Pb,hb,&qb);
            InsFirst(Pa,ha,&qb);
            qb = NextPos(*Pb,hb);
            ha = NextPos(*Pa,ha);
            break;
        }//switch
    }//while
    if(!ListEmpty(*Pb))
        Append(Pa,&qb);
    FreeNode(hb);
}

void TraversePolyn(polynomial p)
{
    Link h;
    h = p.head->next;
    while(h){
        printf("%dx^%d",h->data.coef,h->data.expn);
        if(h->next)
            printf(" + ");
        h = h->next;
    }
    printf("\n");
}

/*******************************主函数部分**************************************/
int main()
{
    polynomial Pa,Pb;

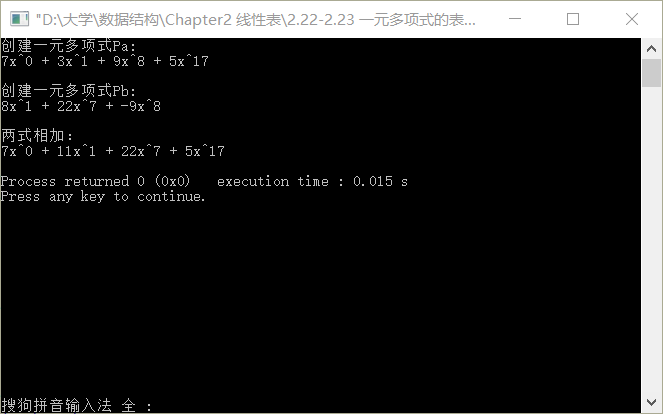
    printf("创建一元多项式Pa:\n");
    CreatePolyn_1(&Pa,4);
    TraversePolyn(Pa);

    printf("\n创建一元多项式Pb:\n");
    CreatePolyn_2(&Pb,3);
    TraversePolyn(Pb);

    printf("\n两式相加：\n");
    AddPolyn(&Pa,&Pb);
    TraversePolyn(Pa);

    return 0;
}