BitMap算法
BitMap
BitMap从字面的意思,很多人认为是位图,其实准确的来说,翻译成基于位的映射。
在所有具有性能优化的数据结构中,大家使用最多的就是hash表,是的,在具有定位查找上具有O(1)的常量时间,多么的简洁优美。但是数据量大了,内存就不够了。
当然也可以使用类似外排序来解决问题的,由于要走IO所以时间上又不行。
所谓的Bit-map就是用一个bit位来标记某个元素对应的Value, 而Key即是该元素。由于采用了Bit为单位来存储数据,因此在存储空间方面,可以大大节省。
其实如果你知道计数排序的话(算法导论中有一节讲过),你就会发现这个和计数排序很像。
bitmap应用
1)可进行数据的快速查找,判重,删除,一般来说数据范围是int的10倍以下。
2)去重数据而达到压缩数据
还可以用于爬虫系统中url去重、解决全组合问题。
BitMap应用:排序示例
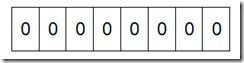
假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复)。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0(如下图:)
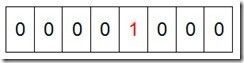
然后遍历这5个元素,首先第一个元素是4,那么就把4对应的位置为1(可以这样操作 p+(i/8)|(0×01<<(i%8)) 当然了这里的操作涉及到Big-ending和Little-ending的情况,这里默认为Big-ending。不过计算机一般是小端存储的,如intel。小端的话就是将倒数第5位置1),因为是从零开始的,所以要把第五位置为一(如下图):
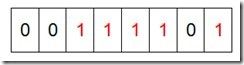
然后再处理第二个元素7,将第八位置为1,,接着再处理第三个元素,一直到最后处理完所有的元素,将相应的位置为1,这时候的内存的Bit位的状态如下:
然后我们现在遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的。
bitmap排序复杂度分析
Bitmap排序需要的时间复杂度和空间复杂度依赖于数据中最大的数字。
bitmap排序的时间复杂度不是O(N)的,而是取决于待排序数组中的最大值MAX,在实际应用上关系也不大,比如我开10个线程去读byte数组,那么复杂度为:O(Max/10)。也就是要是读取的,可以用多线程的方式去读取。时间复杂度方面也是O(Max/n),其中Max为byte[]数组的大小,n为线程大小。
空间复杂度应该就是O(Max/8)bytes吧
BitMap算法流程
假设需要排序或者查找的最大数MAX=10000000(lz:这里MAX应该是最大的数而不是int数据的总数!),那么我们需要申请内存空间的大小为int a[1 + MAX/32]。
其中:a[0]在内存中占32为可以对应十进制数0-31,依次类推:
bitmap表为:
a[0]--------->0-31
a[1]--------->32-63
a[2]--------->64-95
a[3]--------->96-127
..........
我们要把一个整数N映射到Bit-Map中去,首先要确定把这个N Mapping到哪一个数组元素中去,即确定映射元素的index。我们用int类型的数组作为map的元素,这样我们就知道了一个元素能够表示的数字个数(这里是32)。于是N/32就可以知道我们需要映射的key了。所以余下来的那个N%32就是要映射到的位数。
1.求十进制数对应在数组a中的下标:
先由十进制数n转换为与32的余可转化为对应在数组a中的下标。
如十进制数0-31,都应该对应在a[0]中,比如n=24,那么 n/32=0,则24对应在数组a中的下标为0。又比如n=60,那么n/32=1,则60对应在数组a中的下标为1,同理可以计算0-N在数组a中的下标。
i = N>>K % 结果就是N/(2^K)
Note: map的范围是[0, 原数组最大的数对应的2的整次方数-1]。
2.求十进制数对应数组元素a[i]在0-31中的位m:
十进制数0-31就对应0-31,而32-63则对应也是0-31,即给定一个数n可以通过模32求得对应0-31中的数。
m = n & ((1 << K) - 1) %结果就是n%(2^K)
3.利用移位0-31使得对应第m个bit位为1
如a[i]的第m位置1:a[i] = a[i] | (1< 如:将当前4对应的bit位置1的话,只需要1左移4位与B[0] | 即可。 Note: 1 p+(i/8)|(0×01<<(i%8))这样也可以? 2 同理将int型变量a的第k位清0,即a=a&~(1< [编程珠玑] 优点: 2. 当数据类似(1,1000,10万)只有3个数据的时候,用bitmap时间复杂度和空间复杂度相当大,只有当数据比较密集时才有优势。 Bloom filter可以看做是对bit-map的扩展。更大数据量的有一定误差的用来判断映射是否重复的算法。[Bloom Filter布隆过滤器] 皮皮blog 1 使用位图法判断整形数组是否存在重复 2 在2.5亿个整数中找出不重复的整数,注,内存不足以容纳这2.5亿个整数 解法一:将bit-map扩展一下,采用2-Bitmap(每个数分配2bit,00表示不存在,01表示出现一次,10表示多次,11无意义)进行,共需内存2^32 * 2 bit=1 GB内存,还可以接受。然后扫描这2.5亿个整数,查看Bitmap中相对应位,如果是00变01,01变10,10保持不变。所描完事后,查看bitmap,把对应位是01的整数输出即可。 [c++直接实现代码大数据:查找不重复的整数 ] 或者我们不用2bit来进行表示,我们用两个bit-map即可模拟实现这个2bit-map,都是一样的道理。 解法二:也可采用与第1题类似的方法,进行划分小文件的方法。然后在小文件中找出不重复的整数,并排序。然后再进行归并,注意去除重复的元素。 解法三:(lz)类似解法2,只是划分时按照快排partition一样划分,直到划分到每个块都可以放入内存中。 [c实现] 2.1 一个序列里除了一个元素,其他元素都会重复出现3次,设计一个时间复杂度与空间复杂度最低的算法,找出这个不重复的元素。 3 已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。 8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==1.2MBytes,这样,就用了小小的1.2M左右的内存表示了所有的8位数的电话) lz觉得这个是应该用计数排序类似的算法吧,而不是bitmap? 4 给40亿个不重复的unsigned int的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那40亿个数当中? 解析:bitmap算法就好办多了。申请512M的内存,一个bit位代表一个unsigned int值,读入40亿个数,设置相应的bit位;读入要查询的数,查看相应bit位是否为1,为1表示存在,为0表示不存在。 Note: unsigned int最大数为2^32 - 1,所以需要2^32 - 1个位,也就是(2^32 - 1) / 8 /10 ^ 9G = 0.5G内存。 逆向思维优化:usinged int只有接近43亿(unsigned int最大值为232-1=4294967295,最大不超过43亿),所以可以用某种方式存没有出现过的3亿个数(使用数组{大小为3亿中最大的数/8 bytes}存储),如果出现在3亿个数里面,说明不在40亿里面。3亿个数存储空间一般小于40亿个。(xx存储4294967296需要512MB, 存储294967296只需要35.16MBxx) 5 给定一个数组a,求所有和为SUM的两个数。 如果数组都是整数(负数也可以,将所有数据加上最小的负数x,SUM += 2x就可以了)。如a = [1,2,3,4,7,8],先求a的补数组[8,7,6,5,2,1],开辟两个数组b1,b2(最大数组长度为SUM/8/2{因为两数满足和为SUM,一个数 皮皮blog lz写的一个比较好的实现 00000000000000000000000000000001 [-44, -3, 2, 3, 5, 7, 32] Python package[bitsets 0.7.9] Python 实现类似C++的bitset类:[Python 实现类似C++的bitset类 ] c++有bitset模块 也可以自己实现:[海量数据处理算法—Bit-Map ] 其实某些语言是对BitMap算法进行了封装的,比如java中对应BitMap的数据结构就有BitSet类。其使用方法相当简单,看看API就ok,还是给个例子吧: [java.util.BitSet代码实现] --------------------- 作者:-柚子皮- 来源:CSDN 原文:https://blog.csdn.net/pipisorry/article/details/62443757?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接! BitMap从字面的意思,很多人认为是位图,其实准确的来说,翻译成基于位的映射。 在所有具有性能优化的数据结构中,大家使用最多的就是hash表,是的,在具有定位查找上具有O(1)的常量时间,多么的简洁优美。但是数据量大了,内存就不够了。 当然也可以使用类似外排序来解决问题的,由于要走IO所以时间上又不行。 所谓的Bit-map就是用一个bit位来标记某个元素对应的Value, 而Key即是该元素。由于采用了Bit为单位来存储数据,因此在存储空间方面,可以大大节省。 其实如果你知道计数排序的话(算法导论中有一节讲过),你就会发现这个和计数排序很像。 1)可进行数据的快速查找,判重,删除,一般来说数据范围是int的10倍以下。 还可以用于爬虫系统中url去重、解决全组合问题。 假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复)。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0(如下图:) 然后遍历这5个元素,首先第一个元素是4,那么就把4对应的位置为1(可以这样操作 p+(i/8)|(0×01<<(i%8)) 当然了这里的操作涉及到Big-ending和Little-ending的情况,这里默认为Big-ending。不过计算机一般是小端存储的,如intel。小端的话就是将倒数第5位置1),因为是从零开始的,所以要把第五位置为一(如下图): 然后再处理第二个元素7,将第八位置为1,,接着再处理第三个元素,一直到最后处理完所有的元素,将相应的位置为1,这时候的内存的Bit位的状态如下: 然后我们现在遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的。 Bitmap排序需要的时间复杂度和空间复杂度依赖于数据中最大的数字。 bitmap排序的时间复杂度不是O(N)的,而是取决于待排序数组中的最大值MAX,在实际应用上关系也不大,比如我开10个线程去读byte数组,那么复杂度为:O(Max/10)。也就是要是读取的,可以用多线程的方式去读取。时间复杂度方面也是O(Max/n),其中Max为byte[]数组的大小,n为线程大小。 空间复杂度应该就是O(Max/8)bytes吧 假设需要排序或者查找的最大数MAX=10000000(lz:这里MAX应该是最大的数而不是int数据的总数!),那么我们需要申请内存空间的大小为int a[1 + MAX/32]。 其中:a[0]在内存中占32为可以对应十进制数0-31,依次类推: 我们要把一个整数N映射到Bit-Map中去,首先要确定把这个N Mapping到哪一个数组元素中去,即确定映射元素的index。我们用int类型的数组作为map的元素,这样我们就知道了一个元素能够表示的数字个数(这里是32)。于是N/32就可以知道我们需要映射的key了。所以余下来的那个N%32就是要映射到的位数。 1.求十进制数对应在数组a中的下标: 如十进制数0-31,都应该对应在a[0]中,比如n=24,那么 n/32=0,则24对应在数组a中的下标为0。又比如n=60,那么n/32=1,则60对应在数组a中的下标为1,同理可以计算0-N在数组a中的下标。 i = N>>K % 结果就是N/(2^K) Note: map的范围是[0, 原数组最大的数对应的2的整次方数-1]。 2.求十进制数对应数组元素a[i]在0-31中的位m: m = n & ((1 << K) - 1) %结果就是n%(2^K) 3.利用移位0-31使得对应第m个bit位为1 如a[i]的第m位置1:a[i] = a[i] | (1< 如:将当前4对应的bit位置1的话,只需要1左移4位与B[0] | 即可。 Note: 1 p+(i/8)|(0×01<<(i%8))这样也可以? 2 同理将int型变量a的第k位清0,即a=a&~(1< [编程珠玑] 优点: 2. 当数据类似(1,1000,10万)只有3个数据的时候,用bitmap时间复杂度和空间复杂度相当大,只有当数据比较密集时才有优势。 Bloom filter可以看做是对bit-map的扩展。更大数据量的有一定误差的用来判断映射是否重复的算法。[Bloom Filter布隆过滤器] 皮皮blog 1 使用位图法判断整形数组是否存在重复 2 在2.5亿个整数中找出不重复的整数,注,内存不足以容纳这2.5亿个整数 解法一:将bit-map扩展一下,采用2-Bitmap(每个数分配2bit,00表示不存在,01表示出现一次,10表示多次,11无意义)进行,共需内存2^32 * 2 bit=1 GB内存,还可以接受。然后扫描这2.5亿个整数,查看Bitmap中相对应位,如果是00变01,01变10,10保持不变。所描完事后,查看bitmap,把对应位是01的整数输出即可。 [c++直接实现代码大数据:查找不重复的整数 ] 或者我们不用2bit来进行表示,我们用两个bit-map即可模拟实现这个2bit-map,都是一样的道理。 解法二:也可采用与第1题类似的方法,进行划分小文件的方法。然后在小文件中找出不重复的整数,并排序。然后再进行归并,注意去除重复的元素。 解法三:(lz)类似解法2,只是划分时按照快排partition一样划分,直到划分到每个块都可以放入内存中。 [c实现] 2.1 一个序列里除了一个元素,其他元素都会重复出现3次,设计一个时间复杂度与空间复杂度最低的算法,找出这个不重复的元素。 3 已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。 8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==1.2MBytes,这样,就用了小小的1.2M左右的内存表示了所有的8位数的电话) lz觉得这个是应该用计数排序类似的算法吧,而不是bitmap? 4 给40亿个不重复的unsigned int的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那40亿个数当中? 解析:bitmap算法就好办多了。申请512M的内存,一个bit位代表一个unsigned int值,读入40亿个数,设置相应的bit位;读入要查询的数,查看相应bit位是否为1,为1表示存在,为0表示不存在。 Note: unsigned int最大数为2^32 - 1,所以需要2^32 - 1个位,也就是(2^32 - 1) / 8 /10 ^ 9G = 0.5G内存。 逆向思维优化:usinged int只有接近43亿(unsigned int最大值为232-1=4294967295,最大不超过43亿),所以可以用某种方式存没有出现过的3亿个数(使用数组{大小为3亿中最大的数/8 bytes}存储),如果出现在3亿个数里面,说明不在40亿里面。3亿个数存储空间一般小于40亿个。(xx存储4294967296需要512MB, 存储294967296只需要35.16MBxx) 5 给定一个数组a,求所有和为SUM的两个数。 如果数组都是整数(负数也可以,将所有数据加上最小的负数x,SUM += 2x就可以了)。如a = [1,2,3,4,7,8],先求a的补数组[8,7,6,5,2,1],开辟两个数组b1,b2(最大数组长度为SUM/8/2{因为两数满足和为SUM,一个数 皮皮blog lz写的一个比较好的实现 00000000000000000000000000000001 [-44, -3, 2, 3, 5, 7, 32] Python package[bitsets 0.7.9] Python 实现类似C++的bitset类:[Python 实现类似C++的bitset类 ] c++有bitset模块 也可以自己实现:[海量数据处理算法—Bit-Map ] 其实某些语言是对BitMap算法进行了封装的,比如java中对应BitMap的数据结构就有BitSet类。其使用方法相当简单,看看API就ok,还是给个例子吧: [java.util.BitSet代码实现] BitMap算法评价
1. 运算效率高,不进行比较和移位;
2. 占用内存少,比如最大的数MAX=10000000;只需占用内存为MAX/8=1250000Byte=1.25M。
缺点:
1. 所有的数据不能重复,即不可对重复的数据进行排序。(少量重复数据查找还是可以的,用2-bitmap)。BitMap算法的拓展
问题及应用实例
判断集合中存在重复是常见编程任务之一,当集合中数据量比较大时我们通常希望少进行几次扫描,这时双重循环法就不可取了。
位图法比较适合于这种情况,它的做法是按照集合中最大元素max创建一个长度为max+1的新数组,然后再次扫描原数组,遇到几就给新数组的第几位置上1,如遇到 5就给新数组的第六个元素置1,这样下次再遇到5想置位时发现新数组的第六个元素已经是1了,这说明这次的数据肯定和以前的数据存在着重复。这种给新数组初始化时置零其后置一的做法类似于位图的处理方法故称位图法。它的运算次数最坏的情况为2N。如果已知数组的最大值即能事先给新数组定长的话效率还能提高一倍。BitMap的实现
Python
import os, sys, array
CWD = os.path.split(os.path.realpath(__file__))[0]
sys.path.append(os.path.join(CWD, '../..'))
def power2n(x):
'''
求比x大且是2的n次方的数
'''
for i in (1, 2, 4, 8, 16, 32): # 支持到64位int型,加上64则可以支持到128等等
x |= x >> i
# print(x + 1)
return x + 1
class BitMap():
def __init__(self):
self.K = 5
self.BIT_NUM = 1 << self.K
self.BIT_TYPE = 'I' # 32位unsighed int存储位。note:可能8位char存储对小数据更好一丢丢
self.shift = 0 # 如果数组中有<0的数,则所有数都要减去最小的那个负数
def fit(self, x):
'''
将数据读入bitmap中存储
'''
MIN_NUM = min(x)
if MIN_NUM < 0:
self.shift = -MIN_NUM # 如果数组中有<0的数,则所有数都要减去最小的那个负数
x = [i + self.shift for i in x]
else:
self.shift = 0
MAX_NUM = max(x)
num_int = power2n(MAX_NUM) >> self.K
num_int = num_int if num_int > 0 else 1 # 至少应该有一个数组
# print(num_int)
self.a = array.array(self.BIT_TYPE, [0] * num_int)
for xi in x:
self.set(xi)
def set(self, xi, value=1):
'''
设置数xi在数组a中对应元素对应的位为1
'''
array_ix = xi >> self.K # 数组的元素位置(从0开始)
bit_ix = xi & ((1 << self.K) - 1) # 数组元素中的bit位置(从0开始),取模
if value == 1:
self.a[array_ix] |= 1 << bit_ix # 对应的第bit_ix位置的2**bit_ix置1
else:
self.a[array_ix] &= ~((1 << bit_ix)) # 对应的第bit_ix位置的2**bit_ix置0
def show_array(self):
for ai in self.a:
print('{:032b}'.format(ai)) # bin(ai)
def search(self, xi):
'''
bitmap查找
'''
if self.shift != 0:
xi += self.shift
array_ix = xi >> self.K
bit_ix = xi & ((1 << self.K) - 1)
if (self.a[array_ix] & (1 << bit_ix)):
flag = True
else:
flag = False
return flag
def sort(self):
'''
bitmap排序
'''
sorted_x = []
for array_ix, ai in enumerate(self.a):
for bit_ix in range(self.BIT_NUM):
# 首先得到该第j位的掩码(0x01<<j),将内存区中的,位和此掩码作与操作。最后判断掩码是否和处理后的结果相同
if (ai & (1 << bit_ix)) == (1 << bit_ix):
sorted_x.append(self.BIT_NUM * array_ix + bit_ix)
# print(sorted_x)
if self.shift != 0:
sorted_x = [i - self.shift for i in sorted_x]
return sorted_x
def test():
bm = BitMap()
bm.fit([-3, -44, 7, 2, 5, 3, 32])
bm.show_array()
print(bm.search(7))
print(bm.search(6))
print(bm.sort())
test()
00000000000010101100001000000000
00000000000000000001000000000000
00000000000000000000000000000000
True
FalseC/C++
Java
import java.util.BitSet;
public class Test{
public static void main(String[] args) {
int [] array = new int [] {1,2,3,22,0,3};
BitSet bitSet = new BitSet(6);
//将数组内容组bitmap
for(int i=0;i
bitSet.set(array[i], true);
}
System.out.println(bitSet.size());
System.out.println(bitSet.get(3));
}
}
对应的bit位如果有对应整数那么通过bitSet.get(x)会返回true,反之false。其中x为BitMap位置下标。BitMap
bitmap应用
2)去重数据而达到压缩数据BitMap应用:排序示例
bitmap排序复杂度分析
BitMap算法流程
bitmap表为:
a[0]--------->0-31
a[1]--------->32-63
a[2]--------->64-95
a[3]--------->96-127
..........
先由十进制数n转换为与32的余可转化为对应在数组a中的下标。
十进制数0-31就对应0-31,而32-63则对应也是0-31,即给定一个数n可以通过模32求得对应0-31中的数。BitMap算法评价
1. 运算效率高,不进行比较和移位;
2. 占用内存少,比如最大的数MAX=10000000;只需占用内存为MAX/8=1250000Byte=1.25M。
缺点:
1. 所有的数据不能重复,即不可对重复的数据进行排序。(少量重复数据查找还是可以的,用2-bitmap)。BitMap算法的拓展
问题及应用实例
判断集合中存在重复是常见编程任务之一,当集合中数据量比较大时我们通常希望少进行几次扫描,这时双重循环法就不可取了。
位图法比较适合于这种情况,它的做法是按照集合中最大元素max创建一个长度为max+1的新数组,然后再次扫描原数组,遇到几就给新数组的第几位置上1,如遇到 5就给新数组的第六个元素置1,这样下次再遇到5想置位时发现新数组的第六个元素已经是1了,这说明这次的数据肯定和以前的数据存在着重复。这种给新数组初始化时置零其后置一的做法类似于位图的处理方法故称位图法。它的运算次数最坏的情况为2N。如果已知数组的最大值即能事先给新数组定长的话效率还能提高一倍。BitMap的实现
Python
import os, sys, array
CWD = os.path.split(os.path.realpath(__file__))[0]
sys.path.append(os.path.join(CWD, '../..'))
def power2n(x):
'''
求比x大且是2的n次方的数
'''
for i in (1, 2, 4, 8, 16, 32): # 支持到64位int型,加上64则可以支持到128等等
x |= x >> i
# print(x + 1)
return x + 1
class BitMap():
def __init__(self):
self.K = 5
self.BIT_NUM = 1 << self.K
self.BIT_TYPE = 'I' # 32位unsighed int存储位。note:可能8位char存储对小数据更好一丢丢
self.shift = 0 # 如果数组中有<0的数,则所有数都要减去最小的那个负数
def fit(self, x):
'''
将数据读入bitmap中存储
'''
MIN_NUM = min(x)
if MIN_NUM < 0:
self.shift = -MIN_NUM # 如果数组中有<0的数,则所有数都要减去最小的那个负数
x = [i + self.shift for i in x]
else:
self.shift = 0
MAX_NUM = max(x)
num_int = power2n(MAX_NUM) >> self.K
num_int = num_int if num_int > 0 else 1 # 至少应该有一个数组
# print(num_int)
self.a = array.array(self.BIT_TYPE, [0] * num_int)
for xi in x:
self.set(xi)
def set(self, xi, value=1):
'''
设置数xi在数组a中对应元素对应的位为1
'''
array_ix = xi >> self.K # 数组的元素位置(从0开始)
bit_ix = xi & ((1 << self.K) - 1) # 数组元素中的bit位置(从0开始),取模
if value == 1:
self.a[array_ix] |= 1 << bit_ix # 对应的第bit_ix位置的2**bit_ix置1
else:
self.a[array_ix] &= ~((1 << bit_ix)) # 对应的第bit_ix位置的2**bit_ix置0
def show_array(self):
for ai in self.a:
print('{:032b}'.format(ai)) # bin(ai)
def search(self, xi):
'''
bitmap查找
'''
if self.shift != 0:
xi += self.shift
array_ix = xi >> self.K
bit_ix = xi & ((1 << self.K) - 1)
if (self.a[array_ix] & (1 << bit_ix)):
flag = True
else:
flag = False
return flag
def sort(self):
'''
bitmap排序
'''
sorted_x = []
for array_ix, ai in enumerate(self.a):
for bit_ix in range(self.BIT_NUM):
# 首先得到该第j位的掩码(0x01<<j),将内存区中的,位和此掩码作与操作。最后判断掩码是否和处理后的结果相同
if (ai & (1 << bit_ix)) == (1 << bit_ix):
sorted_x.append(self.BIT_NUM * array_ix + bit_ix)
# print(sorted_x)
if self.shift != 0:
sorted_x = [i - self.shift for i in sorted_x]
return sorted_x
def test():
bm = BitMap()
bm.fit([-3, -44, 7, 2, 5, 3, 32])
bm.show_array()
print(bm.search(7))
print(bm.search(6))
print(bm.sort())
test()
00000000000010101100001000000000
00000000000000000001000000000000
00000000000000000000000000000000
True
FalseC/C++
Java
import java.util.BitSet;
public class Test{
public static void main(String[] args) {
int [] array = new int [] {1,2,3,22,0,3};
BitSet bitSet = new BitSet(6);
//将数组内容组bitmap
for(int i=0;i
bitSet.set(array[i], true);
}
System.out.println(bitSet.size());
System.out.println(bitSet.get(3));
}
}
对应的bit位如果有对应整数那么通过bitSet.get(x)会返回true,反之false。其中x为BitMap位置下标。