论文阅读之Arcface

Arcface论文阅读

###前言

近年来随着硬件计算能力的大爆发，在高性能计算的支持下深度学习有了革命性的进步，在互联网大数据的保证下深度学习有了源源不断的动力，优秀的网络结构被不断提出，深度学习技术已被推向 时代浪潮。在深度学习的分支领域，计算机视觉领域当中，人脸识别技术的发展依然是工业界、学术界重点关注的对象。在ResNet在2015年被提出后，越来越多优秀的网络基于ResNet进行优化更新也已取得卓越的成就，而在网络结构进一步升级优化有困难的情况下，研究者逐步将目光转向损失函数这一指挥棒上。

文章[ArcFace:Additive Angular Margin Loss for Deep Face Recognition]的作者提出的Angular Margin Loss在继SoftmaxLoss、Center Loss、A-Softmax Loss、Cosine Margin Loss之后有更加卓越的表现，同时作者也对这一“卓越表现”予以了论证。

论文地址：https://arxiv.org/abs/1801.07698

Code：https://github.com/deepinsight/insightface

人脸识别流程

人脸识别分为四个过程：人脸检测、人脸对齐、特征提取、特征匹配。其中，特征提取作为人脸识别最关键的步骤，提取到的特征更偏向于该人脸“独有”的特征，对于特征匹配起到举足轻重的作用，而我们的网络和模型承担着提取特征的重任，优秀的网络和训练策略使得模型更加健壮。

但在Resnet网络表现力十分优秀的情况下，要提高人脸识别模型的性能，除了优化网络结构，修改损失函数是另一种选择，优化损失函数可以使模型从现有数据中学习到更多有价值的信息。

而在我们以往接触的分类问题有很大一部分使用了Softmax loss来作为网络的损失层，实验表明Softmax loss考虑到样本是否能正确分类，而在扩大异类样本间的类间距离和缩小同类样本间的类内距离的问题上有很大的优化空间，因而作者在Arcface文章中讨论了Softmax到Arcface的变化过程，同时作者还指出了数据清洗的重要性，改善了Resnet网络结构使其“更适合”学习人脸的特征。

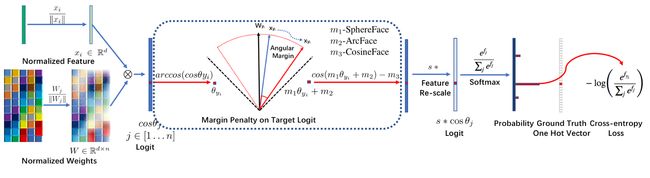
如下是ArcFace的输入到输出流程：

上图的处理流程是这样子的，这里假设我们的样本类别数为$n$，我们的输入数据x的维度为$d$，模型权重$w$的维度为$d\cdot n$，我们首先对我们的样本$x$和权重$w$进行归一化，归一化之后样本经过网络最后得到$1\cdot n$维的全连接输出，输出后计算得到Target Logit再乘以归一化参数$s$再经过Softmax计算得到Prob。

数据

在训练过程中，神经网络都是基于我们的训练数据学习特征的，既然是从训练数据学习特征，最终的方向自然是逼近最终数据的最真实的特征，也就是说，我们数据最原始是什么样子，我们的网络的极限就是什么样子，它不能超越数据本身，而研究者在做的事情，也就是使得网络最后能更加逼近“极限”。所以数据在深度学习中扮演着极其重要的角色，所以文章中强调了干净的数据（数据清洗）的重要性。

这里列举一些文章中提到的开源数据集：

VGG2

VGG2Face人脸数据集包含有训练集8631个人的脸（总量有3141890张人脸），测试集包含有500个人的脸（总量有169396张人脸），属于高质量数据集。

MS-Celeb-1M

MS1M数据集包含有大约10万个人的脸（大约有1千万张人脸），但是数据集中包含有很多的“噪声”，所以作者对MS1M做了数据清洗，最终作者清洗得到的干净的数据包含有8.5万个人的脸（包含有380万张人脸）。

MegaFace

MegaFace数据集包含有69万个人的脸（包含大约有100万张人脸），所有数据由华盛顿大学从Flickr上组织收集。MegaFace是第一个在百万规模级别的面部识别算法的测试基准，这个项目旨在研究当数据库规模提升数个量级时，现有的脸部识别系统能否维持可靠的准确率。MegaFace是目前最为权威、最热门的评价人脸识别性能，特别是海量人脸识别检索性能的基准参照之一。

LFW

LFW（Labeled Faces in the Wild）数据集包含了从网络收集的13000张人脸图像，每张图像都以被拍摄的人名命名。其中，有1680个人有两个或两个以上不同的照片。LFW主要侧重于对比两张人脸照片是否具有相同身份不同。

CPF

CFP（Celebrities in Frontal Profile ）数据集是美国名人的人脸数据集，其中包含有500个人物对象，有他们的10张正面照以及4张形象照，因此在作为人物比对验证的时候，作者选用了最有挑战的正面照与形象照作为验证集（CFP，Frontal-Profile，CFP-FP ）。

AgeDB

AgeDB（Age Database ）数据集包含有440个人的脸（包含有12240张人脸），但其中包含有不同人的不同年龄阶段的照片，最小从3岁到最大101岁时期的照片，每个对象的平均年龄范围为49年。作者采用和LFW一样的对比验证方式。

最后，作者在网络训练过程中采用了VGG2以及MS1M作为训练集，选用了LFW、CPF以及AgeDB作为验证集，最终使用MegaFace作为评测标准。

损失层

关于Loss对于网络的影响，最直观的就是通过计算Loss反传梯度来实现对模型参数的更新，不同的Loss可以使模型更加侧重于学习到数据某一方面的特性，并在之后能够更好地提取到这一“独有”的特征，因此Loss对于网络优化有导向性的作用。

而在近年来人脸识别领域，优化Loss对于最终结果的提高有很大的帮助，从Center Loss的提出，到SphereFace，CosineFace，InsightFace等都有在损失函数这一环节提出新的解决方案，它们的出现对于人脸识别的发展做出了不可磨灭的贡献。

无论是SphereFace、CosineFace还是ArcFace的损失函数，都是基于传统的softmax loss进行修改得到的，所以想要理解ArcFace，需要对之前的损失函数有一定理解。

Softmax Loss

$$L_S=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{W_{y_i}^T{x}_i+b_{y_i}}}{\sum _{j=1}^n{e}^{W_j^T{x}_i+b_j}}\right)$$
这是我们传统的Softmax公式，其中，$W_j^T{x}_i+b_j$ 代表我们的全连接层输出，我们在使损失$L_S$下降的过程中，则必须提高我们的$W_{y_i}^T{x}_i+b_{y_i}$所占有的比重，从而使得该类的样本更多地落入到该类的决策边界之内。

而这种方式主要考虑样本是否能正确分类，缺乏类内和类间距离的约束。

在[A Discriminative Feature Learning Approach for Deep Face Recognition]这篇文章中，作者使用了一个比LeNet更深的网络结构，用Mnist做了一个小实验来证明Softmax学习到的特征与理想状态下的差距。

实验结果表明，传统的Softmax仍存在着很大的类内距离，也就是说，通过对损失函数增加类内距离的约束，能达到比更新现有网络结构更加事半功倍的效果。于是，[A Discriminative Feature Learning Approach for Deep Face Recognition]的作者提出了Center Loss，并从不同角度对结果的提升做了论证。

Center Loss

$$L_C=-\frac{1}{2}\sum _{i=1}^m{||x_i-c_{y_i}||}^2$$

$$\Delta c_j=\frac{\sum _{i=1}^m\delta (y_i=j)\cdot (c_j-x_i)}{1+\sum _{i=1}^m\delta (y_i=j)}$$

Center Loss的整体思想是希望一个batch中的每个样本的feature离feature 的中心的距离的平方和要越小越好，也就是类内距离要越小越好。作者提出，最终的损失函数包含softmax loss和center loss，用参数λ来控制二者的比重，如下面公式所示：
$$L=L_S+L_C=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{W_{y_i}^T{x}_i+b_{y_i}}}{\sum _{j=1}^n{e}^{W_j^T{x}_i+b_j}}\right)+\frac{\lambda }{2}\sum _{i=1}^m{||x_i-c_{y_i}||}^2$$

因而，加入了Softmax Loss对正确类别分类的考虑以及Center Loss对类内距离紧凑的考虑，总的损失函数在分类结果上有很好的表现力。以下是作者继上个实验后使用新的损失函数并调节不同的参数$\lambda$得到的实验结果，可以看到，加入了Center Loss后增加了对类内距离的约束，使得同个类直接的样本的类内特征距离变得紧凑。

A-Softmax Loss(SphereFace)

Center Loss的出现，使得人脸识别的研究转向损失函数的改进，对于之前的损失函数，研究发现Softmax Loss学习到的特征分辨性不够强，Center Loss考虑到了使得类内紧凑，却不能使类间可分，而Contrastive Loss、Triplet Loss增加了时间上的消耗，[SphereFace: Deep Hypersphere Embedding for Face Recognition]这篇文章的作者提出了A-Softmax Loss。

在Softmax Loss中，由$W^{T}x=||W||\cdot ||x||\cdot cos\theta$ 知，特征向量相乘包含由角度信息，即Softmax使得学习到的特征具有角度上的分布特性，为了让特征学习到更可分的角度特性，作者对Softmax Loss进行了一些改进。
$$L_{Softmax}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{||W_{y_i}||\cdot ||x_i||\cdot cos{\theta }_{y_i}+b_{y_i}}}{\sum _{j=1}^n{e}^{||W_j||\cdot ||x_i||\cdot cos{\theta }_j+b_j}}\right)$$

$$L_{modifie{d}_0}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{||x_i||\cdot cos{\theta }_{y_i}}}{e^{||x_i||\cdot cos{\theta }_{y_i}}+\sum _{j=1,j̸=y_i}^n{e}^{||x_i||\cdot cos{\theta }_j}}\right)$$

其中，作者在$L_{modified_0} $中约束了$||W||=1$并且令 $b_j=0$ ,并将 $e^{||x_i||\cdot cos{\theta }_{y_i}}$ 从$\sum _{j=1}^n{e}^{||x_i||\cdot cos{\theta }_j}$区分出来，就是为了让特征学习到更可分的角度特性。通过这样的损失函数学习，可以使得学习到的特征具有更明显的角分布，因为决策边界只与角相关。

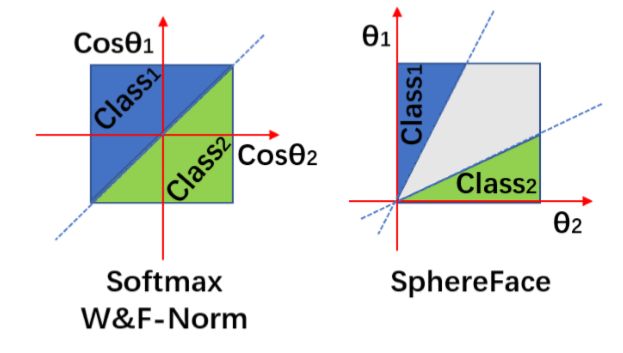
对于Softmax而言，希望能有$cos({\theta }_1)>cos({\theta }_2)$，所以作者增加了在角度空间中对损失函数的约束$cos(t\cdot {\theta }_1)>cos({\theta }_2)$，也就是要把同类数据压缩在一个紧致的空间，同时拉大类间差距。
$$L_{modifie{d}_1}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{||x_i||\cdot cos(t\cdot {\theta }_{y_i})}}{e^{||x_i||\cdot cos(t\cdot {\theta }_{y_i})}+\sum _{j=1,j̸=y_i}^n{e}^{||x_i||\cdot cos{\theta }_j}}\right),{\theta }_{y_i}\in [0,\frac{\pi }{t}]$$

由于$cos\theta$在$[0,\pi ]$上单调递减，因此$\theta$有上界，为了使得这个函数随角度单调递减，作者构造一个函数去代替$cos\theta$。
$$L_{SphereFace}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{||x_i||\cdot \phi ({\theta }_{y_i})}}{e^{||x_i||\cdot \phi ({\theta }_{y_i})}+\sum _{j=1,j̸=y_i}^n{e}^{||x_i||\cdot cos{\theta }_j}}\right),{\theta }_{y_i}\in [0,\frac{\pi }{t}]$$

$$\phi ({\theta }_{y_i})=(-1{)}^{k}cos(t\cdot {\theta }_{y_i})-2k,{\theta }_{y_i}\in [\frac{k\pi }{t},\frac{(k+1)\pi }{t}],k\in [0,t-1]$$

在SphereFace的实际训练过程中，作者发现引入Softmax约束可以保证模型的收敛性。因此，对$\phi ({\theta }_{y_i})$函数做了变更，并同时用参数λ来控制二者的比重。
$$\phi ({\theta }_{y_i})=\frac{(-1{)}^{k}cos(t\cdot {\theta }_{y_i})-2k+\lambda \cdot cos({\theta }_{y_i})}{1+\lambda }$$

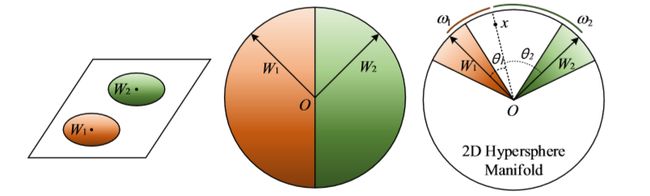
$t$的大小是控制同一类点聚集的程度，从而控制了不同类之间的距离。如图可以看出不同的$t$的取值对映射分布的影响（不同的类位于一个单位超球表面的不同区域）

后续的F-Norm SphereFace对SphereFace做了更新，仅注重从数据中得到的角度信息，而不考虑特征向量的值，所以采用了$s = 64 $作为特征归一化参数替代了$||x||$，因此公式更新为：
$$L_{F-Norm-SphereFace}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{s\cdot \phi ({\theta }_{y_i})}}{e^{s\cdot \phi ({\theta }_{y_i})}+\sum _{j=1,j̸=y_i}^n{e}^{s\cdot cos{\theta }_j}}\right),{\theta }_{y_i}\in [0,\frac{\pi }{t}]$$

而这种采用了$s = 64 $作为特征归一化参数替代了$||x||$的思想也被Cosine Loss和Arcface Loss沿用，即相对于距离信息更加关注角度信息。

Cosine Margin Loss

$$L_{Cosine}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{s\cdot (cos({\theta }_{y_i})-t)}}{e^{s\cdot (cos({\theta }_{y_i})-t)}+\sum _{j=1,j̸=y_i}^n{e}^{s\cdot cos{\theta }_j}}\right)$$
与SphereFace相比，CosineFace最明显的变化就是将$cos(t\cdot {\theta }_{y_i})$中的$t$提出来变成$cos({\theta }_{y_i})-t$，与之前相比，这样有几个明显的优势。

• 相对于SphereFace而言要更加容易实现，移除了$\phi ({\theta }_{y_i})$，减少了复杂的参数计算
• 去除了Softmax监督约束，训练过程变得简洁同时也能够实现收敛
• 模型性能有明显的改善

Angular Margin Loss

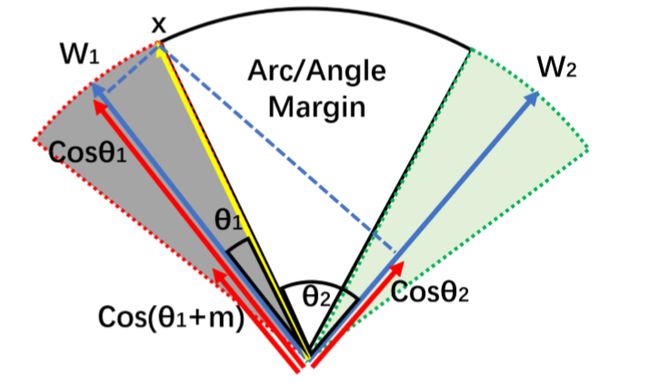
尽管在余弦范围到角度范围的映射具有一对一的关系，但他们之间仍有不同之处，事实上，实现角度空间内最大化分类界限相对于余弦空间而言具有更加清晰的几何解释性，角空间中的边缘差距也相当于超球面上的弧距。

于是，作者提出了Angular Margin Loss，将角度边缘$t$置于$cos(\theta )$函数内部，使得$cos(\theta +t)$在$\theta \in [0,\pi -t]$范围内要小于$cos(\theta )$，这一约束使得整个分类任务的要求变得更加苛刻。

对于$L_{Arcface} $，在满足$W_j=\frac{W_j}{||W_j||},x_i=\frac{x_i}{||x_i||},cos{\theta_i}=W_j^Tx_i$的情况下，其损失计算公式为
$$L_{Arcface}=-\frac{1}{m}\sum _{i=1}^m\log \left(\frac{e^{s\cdot (cos({\theta }_{y_i}+t))}}{e^{s\cdot (cos({\theta }_{y_i}+t))}+\sum _{j=1,j̸=y_i}^n{e}^{s\cdot cos{\theta }_j}}\right)$$
对于$cos(\theta +t)$可以得到$cos(\theta +t)=cos\theta cost-sin\theta sint$，对比CosineFace的$cos(\theta )-t$，ArcFace中的$cos(\theta +t)$不仅形式简单，并且还动态依赖于$sin\theta$，使得网络能够学习到更多的角度特性。

Loss对比分析

为了研究 SphereFace、 CosineFace 和ArcFace是如何提高人脸识别的效果，作者使用了 LResNet34E-IR网络和M1SM人脸数据集分别使用不同的损失函数对网络进行训练，客观分析了其中的影响。

上图的Target Logit Curve描绘了随着角度值$\theta$的变化，对于$L_{Cosine}=-\frac{1}{N}\sum _{i=1}^N\log \left(\frac{e^{s\cdot (cos({\theta }_{y_i})-m)}}{e^{s\cdot (cos({\theta }_{y_i})-m)}+\sum _{j=1,j̸=y_i}^n{e}^{s\cdot cos{\theta }_j}}\right)$,其中的Target Logit 也就是指$cos({\theta }_{y_i})-m$的值，$s$是归一化参数，在$W_j=\frac{W_j}{||W_j||},x_i=\frac{x_i}{||x_i||},cos{\theta }_i=W_j^T{x}_i$条件下，${\theta }_{y_i}$是输入向量与权重在超平面中的夹角，同理，对于$L_{Arcface}=-\frac{1}{N}\sum _{i=1}^N\log \left(\frac{e^{s\cdot (cos({\theta }_{y_i}+m))}}{e^{s\cdot (cos({\theta }_{y_i}+m))}+\sum _{j=1,j̸=y_i}^n{e}^{s\cdot cos{\theta }_j}}\right)$来说，Target Logit 对应着$cos({\theta }_{y_i}+m)$的值，也就意味着，在$\theta \in [0^{\circ },30^{\circ }]$时，CosineFace的曲线要低于ArcFace，也就是在$\theta \in [0^{\circ },30^{\circ }]$范围内CosineFace对于网络的“惩罚”要大于ArcFace，再看$\theta \in [30^{\circ },90^{\circ }]$范围内ArcFace的曲线要低于CosineFace，也就是说在$\theta \in [30^{\circ },90^{\circ }]$内ArcFace对于网络的“惩罚”要大于CosineFace（由下面的$\theta$分布图可知$\theta$在$90^{\circ }$以上范围基本没有，可以忽略）。

而作者提供了训练开始时，中间以及收敛后的$\theta$的分布图，可以看到，在网络收敛的情况下，ArcFace和CosineFace的$\theta$分布基本在$[30^{\circ },60^{\circ }]$范围内，同时，ArcFace和CosineFace的$\theta$中心值要更靠左一点，虽然在$\theta \in [0^{\circ },30^{\circ }]$范围内CosineFace对于网络的“惩罚”要大于ArcFace，但是由最终结果可以看出，收敛时$\theta$达到$[0^{\circ },30^{\circ }]$范围内的数量很少，相对于$[30^{\circ },60^{\circ }]$范围内可以忽略，而在ArcFace对于网络的“惩罚”要大于CosineFace的$\theta \in [30^{\circ },60^{\circ }]$范围内分布着绝大多数的$\theta$。

我们已经由$\theta$的分布图可知在收敛的时候ArcFace的$\theta$中心值与CosineFace相比要偏左一点，同时，由上图可知，收敛的时候红色实线要高于蓝色和黄色实线，也就意味着，收敛的时候ArcFace相对于其他Loss使得同一类更加“紧凑”，相对于其他的Loss实现了将同一个类压缩到一个更紧致的空间，更密集，使得网络学习到的特征具有更明显的角分布特性。

网络

为了衡量怎样的网络更适合人脸识别，作者在基于VGG2Face作为训练集和使用Softmax作为损失函数的情况下对Resnet网络做了不同的设置，以期望能达到最好的效果。

作者用了8块特斯拉P40的显卡，设置训练时的总的Batch Size为512，同时学习率从0.1开始在分别在10万、14万、16万次迭代下降一个量级，设置了总的迭代为20万次，momentum 动量为0.9，权值衰减为 5e−4 。

PS：实验表明采用权值衰减值为5e−4效果最好。

####Input selects L

大多数的卷积神经网络为完成Image-Net的分类任务而设计的，所以网络会采用224x224的输入，然而作者所用的人脸大小为112x112，如果直接将112x112的数据作为预训练模型的输入会使得原本最后提取到的特征维度是7x7变成3x3，因此作者将预训练模型的第一个7x7的卷积层（stride=2）替换成3x3的卷积层（stride=1），这样第一个卷积层就不会将输入的维度缩减，因此最后还是能得到7x7的输入，如下图所示，实验中将修改后的网络在命名上加了字母“L”，比如SE-LResNet50D。

####Output selects E

对于网络的最后几层，不同的输出可能会影响模型的性能，因此作者对Option-A到Option-E分别做了测试，在测试过程中，利用两个特征向量对距离进行计算。在识别与验证的过程中采用了最近邻与阈值比较法。

• Option-A: Use global pooling layer(GP).
• Option-B:Use one fullyconnected(FC) layer after GP.
• Option-C: Use FC-Batch Normalisation (BN) after GP.
• Option-D: Use FC-BN-Parametric Rectified Linear Unit (PReLu) after GP.
• Option-E: Use BN-Dropout-FC-BN after the last convolutional layer.

经过对比结果得知，使用Option-E模型能取得更好的表现。

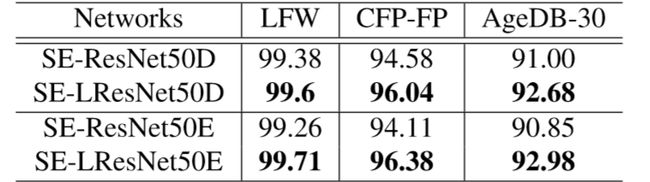
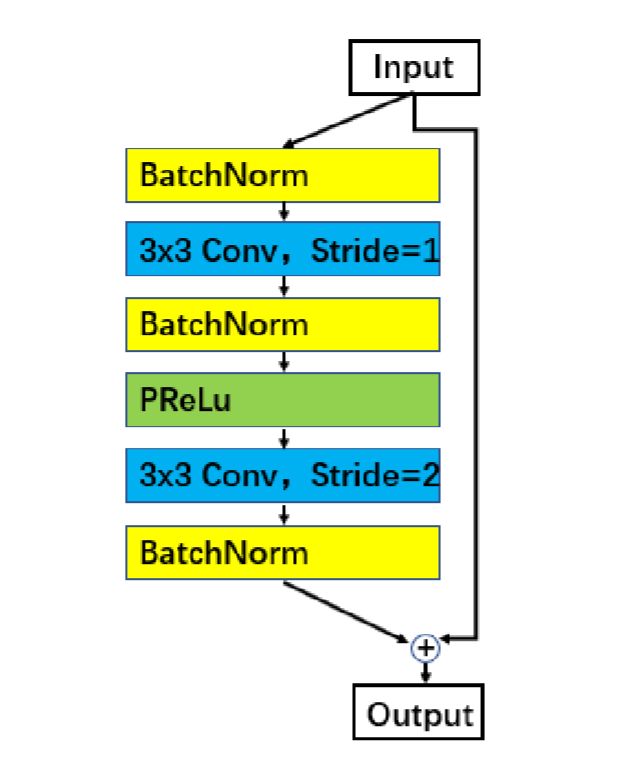
####Block selects IR

作者改善了Resnet网络的残差块使其更适合人脸识别模型的训练，采用 BN-Conv-BN-PReLu-Conv-BN 结构作为残差块，并在残差块中将第一个卷积层的步长从2调整到1，激活函数采用PReLu替代了原来的ReLu。采用修改过的残差块的模型作者在后面添加了“IR”以作为标识。

同样实验表明，采用Option-E与改善后的残差块使得模型表现有明显的提升。

Network Setting Conclusions

综上所述，最终在Resnet网络上做出了3项改进，第一是将第一个7x7的卷积层（stride=2）替换成3x3的卷积层（stride=1），第二是采用了Option-E输出，第三是使用了改善后的残差块。

评估

作者同时对比测试了其他主流的网络结构，有MobileNet、Inception-Resnet-V2、DenseNet、Squeeze and excitation networks (SE)以及Dual path Network (DPN)，评价的标准由精确度、速度以及模型大小组成。

同时，MegaFace作为百万规模级别的面部识别算法的测试基准，作者以LResNet100E-IR作为网络结构，以MS1M作为训练集，分别对比了不同损失函数在MegaFace上的表现，其中最后两列括号中有“R”是代表清洗过的MegaFace，Rank1指标代表第一次命中率，VR@FAR代表在误识率FAR上的TAR，也就是说第一次命中率Rank1越高越好，VR@FAR越高越好。